目录
- 最小生成树算法总览
- 最小生成树的定义及性质
- Prim(普利姆)算法
- 1.朴素Prim算法
- 算法步骤
- 2.堆优化Prim算法
- 算法步骤
- 3.算法运用
- Prim算法求最小生成树
- 流程实现
- 朴素Prim的代码实现
- 堆优化Prim的代码实现
- Kruskal(克鲁斯卡尔)算法
- 1.算法步骤
- 2.算法运用
- Kruskal算法求最小生成树
最小生成树算法总览

最小生成树的定义及性质
最小生成树(Minimum Spanning Tree,简称MST)是图论中的一个概念。给定一个连通的无向图,最小生成树是指包含图中所有顶点的一棵树,且该树的所有边的权重之和最小。
最小生成树的基本定义和性质:
- 连通性:最小生成树必须包含图中的所有顶点,并且通过边将它们连接起来,确保整个图是连通的,即任意两个顶点之间都有路径。(一颗有 n 个顶点的生成树有且仅有 n−1 条边,如果生成树中再添加一条边,则必定成环。)
- 无环:最小生成树是一棵树,所以不能包含任何环(即回路)。
- 最小权重:最小生成树的边权重之和应当尽可能地小。在有多个满足条件的最小生成树时,它们的权重之和是相同的。

实际的场景:
最小生成树在现实生活和计算机科学中有广泛的实际运用场景。以下是一些常见的应用场景:
-
网络设计与通信:在通信网络、电信和计算机网络的设计中,最小生成树用于确定连接所有节点的最优路径,以确保数据传输的高效性和稳定性。
-
电力传输:在电力系统中,最小生成树可用于确定电力线路的布置,确保所有地区都能得到电力供应,同时最小化电力线路的长度和损耗。
-
交通规划:在城市交通规划中,最小生成树可以用来规划公交线路或道路网络,以实现最短路径和最小交通拥堵。
-
管道布置:在石油、天然气等管道网络的布置中,最小生成树可用于确定最优的管道布置,以最小化材料和成本的使用。
-
无线传感器网络:在无线传感器网络中,传感器节点需要有效地传输数据到基站,通过最小生成树可以构建出最优的通信路径,延长网络寿命。
-
图像分割:在计算机视觉领域,图像分割问题可以转化为最小生成树问题,用于将图像分成连通的区域,有助于图像处理和分析。
-
电路板设计:在电路板布线时,最小生成树可用于确定元件之间的最优连接方式,以最小化电路的面积和布线的复杂性。
-
聚类分析:在数据挖掘和机器学习中,最小生成树可以用于聚类分析,将相似的数据点连接在一起形成簇。
Prim(普利姆)算法
1.朴素Prim算法
朴素Prim算法(Naive Prim Algorithm),也称为简单Prim算法,是用于求解无向图的最小生成树的一种基本而直观的算法。该算法是以其发明者之一、计算机科学家Jarník的名字来命名的,也被称为Jarník算法。
时间复杂度:
O
(
n
2
)
O(n^2)
O(n2)
算法步骤
- 选择一个起始节点作为最小生成树的起点。
- 将该起始节点加入最小生成树集合,并将其标记为已访问。
- 在所有与最小生成树集合相邻的边中,选择权重最小的边和它连接的未访问节点。
- 将该边和节点加入最小生成树集合,并将该节点标记为已访问。
- 重复步骤3和步骤4,直到最小生成树集合包含了图中的所有节点。
2.堆优化Prim算法
时间复杂度: O ( m log n ) O(m \log n) O(mlogn)
算法步骤
- 初始化 d i s t dist dist 数组为 I N F INF INF,表示所有节点到集合的距离为无穷大。
- 创建一个小根堆,堆中的元素为( d i s t dist dist 值, 节点编号)。
- 堆中先插入 ( 0 , 1 ) (0, 1) (0,1) 表示节点1进入集合, d i s t dist dist 值为 0 0 0。
- 每次从堆中取出 d i s t dist dist 值最小的元素 ( d , u ) (d, u) (d,u),将u加入集合。
- 对 u u u 相邻的所有节点 v v v,更新 d i s t [ v ] = m i n ( d i s t [ v ] , g [ u ] [ v ] ) dist[v] = min(dist[v], g[u][v]) dist[v]=min(dist[v],g[u][v]),并更新堆中的相应元素。
- 重复步骤 4 、 5 4、5 4、5,直到所有节点都加入集合。
- 最后根据取出的 d i s t dist dist 值之和求得最小生成树权重。
3.算法运用
Prim算法求最小生成树
题目描述:
给定一个
n
n
n 个点
m
m
m 条边的无向图,图中可能存在重边和自环,边权可能为负数。
求最小生成树的树边权重之和,如果最小生成树不存在则输出 i m p o s s i b l e impossible impossible。
给定一张边带权的无向图 G = ( V , E ) G=(V,E) G=(V,E),其中 V V V 表示图中点的集合, E E E 表示图中边的集合, n = ∣ V ∣ n=|V| n=∣V∣, m = ∣ E ∣ m=|E| m=∣E∣。
由 V V V 中的全部 n n n 个顶点和 E E E 中 n − 1 n−1 n−1 条边构成的无向连通子图被称为 G G G 的一棵生成树,其中边的权值之和最小的生成树被称为无向图 G G G 的最小生成树。
输入格式:
第一行包含两个整数
n
n
n 和
m
m
m。
接下来 m m m 行,每行包含三个整数 u , v , w u,v,w u,v,w,表示点 u u u 和点 v v v 之间存在一条权值为 w w w 的边。
输出格式:
共一行,若存在最小生成树,则输出一个整数,表示最小生成树的树边权重之和,如果最小生成树不存在则输出 impossible。
数据范围:
1
≤
n
≤
500
,
1
≤
m
≤
1
0
5
1≤n≤500,1≤m≤10^5
1≤n≤500,1≤m≤105,图中涉及边的边权的绝对值均不超过
10000
10000
10000。
输入样例:
4 5
1 2 1
1 3 2
1 4 3
2 3 2
3 4 4
输出样例:
6
流程实现
我们将图中各个节点用数字
1
∼
n
1∼n
1∼n 编号。
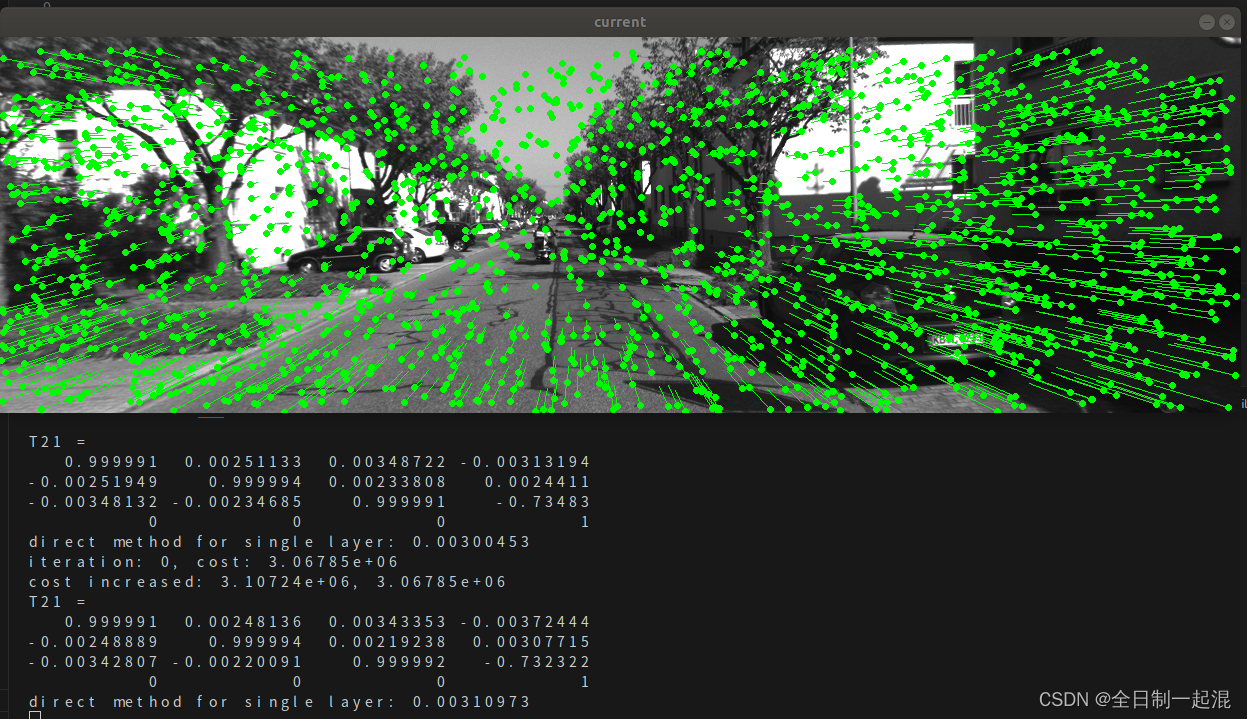
要将所有景点连通起来,并且边长之和最小,步骤如下:
①用一个
s
t
st
st 数组表示节点是否已经连通。
s
t
[
i
]
st[i]
st[i] 为真,表示已经连通,
s
t
[
i
]
st[i]
st[i] 为假,表示还没有连通。初始时,
s
t
st
st 各个元素为假。即所有点还没有连通。用一个
d
i
s
t
dist
dist 数组保存各个点到连通部分的最短距离,
d
i
s
t
[
i
]
dist[i]
dist[i] 表示 i 节点到连通部分的最短距离。初始时,
d
i
s
t
dist
dist 数组的各个元素为无穷大。用一个 pre 数组保存节点的是和谁连通的。
p
r
e
[
i
]
=
k
pre[i]=k
pre[i]=k 表示节点
i
i
i 和节点
k
k
k 之间需要有一条边。初始时,
p
r
e
pre
pre 的各个元素置为 −1。
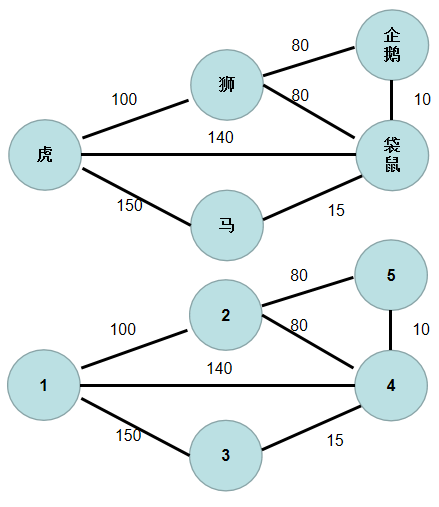
②从
1
1
1 号节点开始扩充连通的部分,
1
1
1 号节点与连通部分的最短距离为
0
0
0,即
d
i
s
t
[
i
]
dist[i]
dist[i] 值为
0
0
0。
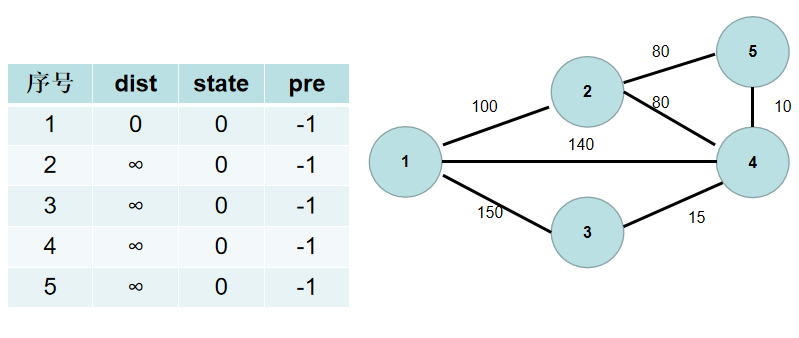
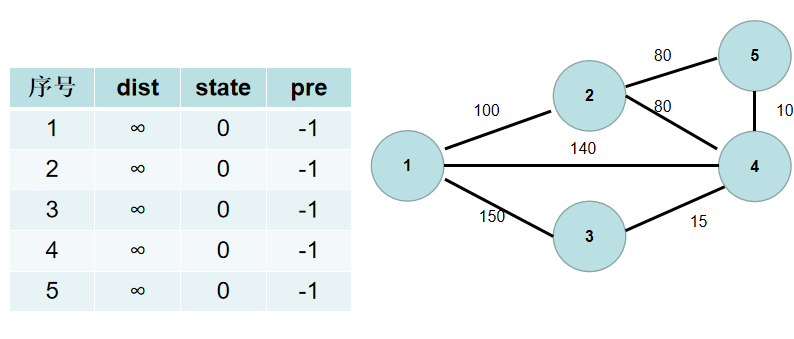
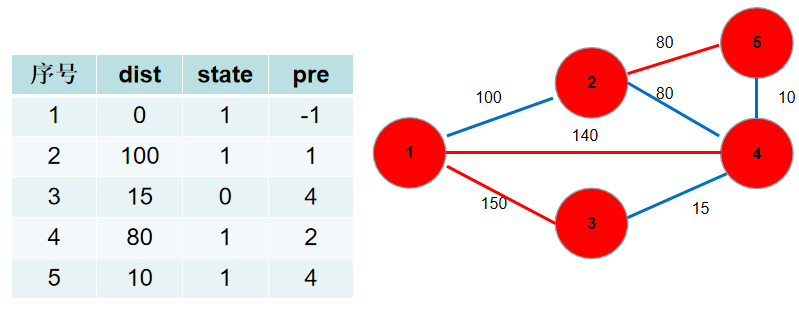
③遍历 d i s t dist dist 数组,找到一个还没有连通起来,但是距离连通部分最近的点,假设该节点的编号是 t t t。 t t t 节点就是下一个应该加入连通部分的节点, s t [ t ] st[t] st[t] 置为 t r u e true true。用青色点表示还没有连通起来的点,红色点表示连通起来的点。这里青色点中距离最小是 d i s t [ 1 ] dist[1] dist[1],因此 s t [ 1 ] st[1] st[1] 置为 t r u e true true。
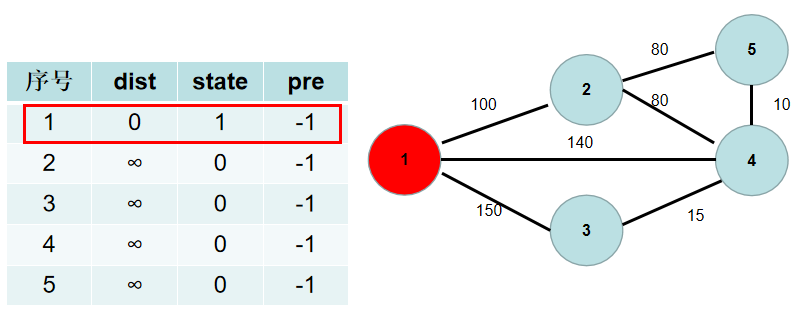
④遍历所有与 t t t 相连但没有加入到连通部分的点 j j j,如果 j j j 距离连通部分的距离大于 t ∼ j t∼j t∼j 之间的距离,即 d i s t [ j ] > g [ t ] [ j ] dist[j]>g[t][j] dist[j]>g[t][j]( g [ t ] [ j ] g[t][j] g[t][j] 为 t ∼ j t∼j t∼j 节点之间的距离),则更新 d i s t [ j ] dist[j] dist[j] 为 g [ t ] [ j ] g[t][j] g[t][j]。这时候表示, j j j 到连通部分的最短方式是和 t t t 相连,因此更新 p r e [ j ] = t pre[j]=t pre[j]=t。
与节点 1 1 1 相连的有 2 , 3 , 4 2, 3, 4 2,3,4 号节点。 1 − > 2 1−>2 1−>2 的距离为 100 100 100,小于 d i s t [ 2 ] dist[2] dist[2], d i s t [ 2 ] dist[2] dist[2] 更新为 100 100 100, p r e [ 2 ] pre[2] pre[2] 更新为 1 1 1。 1 − > 4 1−>4 1−>4 的距离为 140 140 140,小于 d i s t [ 4 ] dist[4] dist[4], d i s t [ 4 ] dist[4] dist[4]更新为 140 140 140, p r e [ 4 ] pre[4] pre[4] 更新为 1 1 1。 1 − > 3 1−>3 1−>3 的距离为 150 150 150,小于 d i s t [ 3 ] dist[3] dist[3], d i s t [ 3 ] dist[3] dist[3] 更新为 150 150 150, p r e [ 3 ] pre[3] pre[3] 更新为 1 1 1。
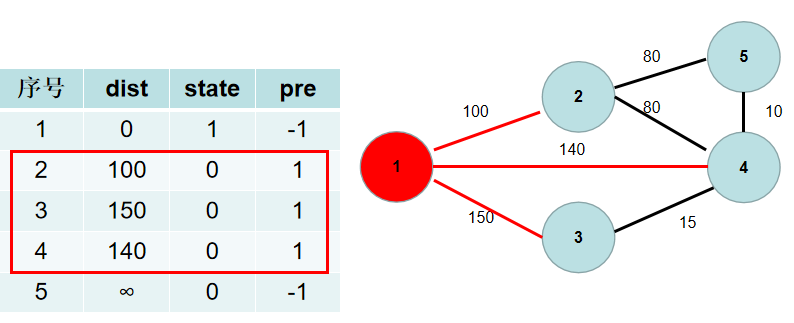
重复 3 − 4 3-4 3−4 步骤,直到所有节点的状态都被置为 1 1 1。这里青色点中距离最小的是 d i s t [ 2 ] dist[2] dist[2],因此 s t [ 2 ] st[2] st[2] 置为 1 1 1。
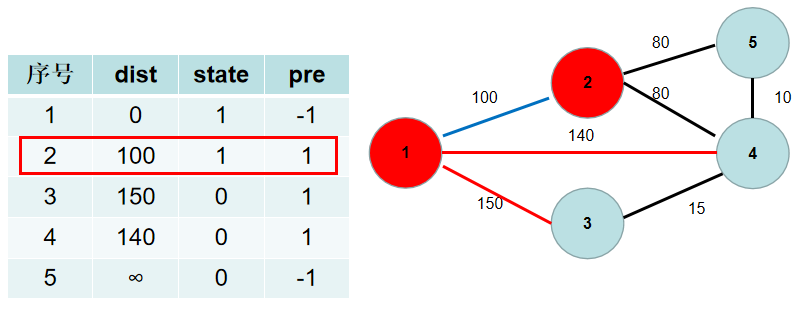
与节点 2 2 2 相连的有 5 5 5, 4 4 4号节点。 2 − > 5 2−>5 2−>5 的距离为 80 80 80,小于 d i s t [ 5 ] dist[5] dist[5],dist[5] 更新为 80 80 80, p r e [ 5 ] pre[5] pre[5] 更新为 2 2 2。 2 − > 4 2−>4 2−>4 的距离为 80 80 80,小于 d i s t [ 4 ] dist[4] dist[4], d i s t [ 4 ] dist[4] dist[4] 更新为 80 80 80, p r e [ 4 ] pre[4] pre[4] 更新为 2 2 2。
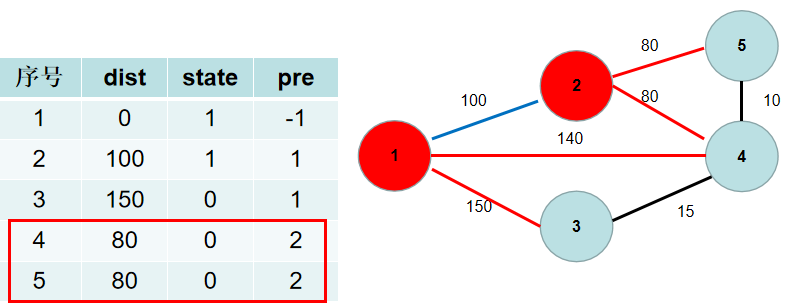
选 d i s t [ 4 ] dist[4] dist[4],更新 d i s t [ 3 ] dist[3] dist[3], d i s t [ 5 ] dist[5] dist[5], p r e [ 3 ] pre[3] pre[3], p r e [ 5 ] pre[5] pre[5]。
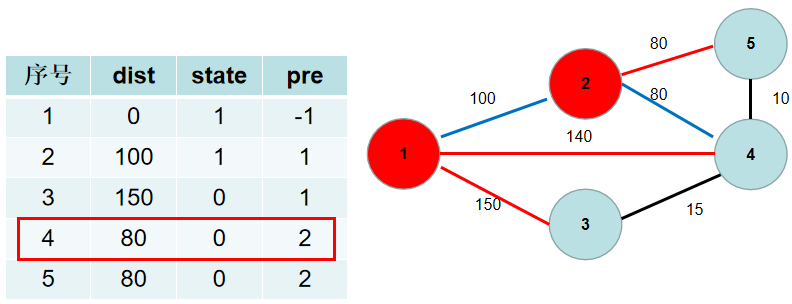
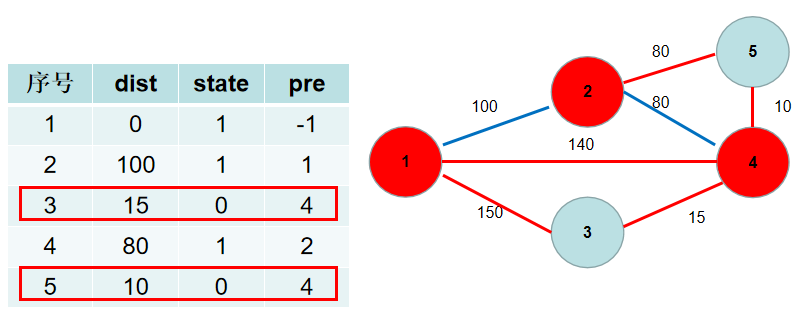
选 d i s t [ 5 ] dist[5] dist[5],没有可更新的。
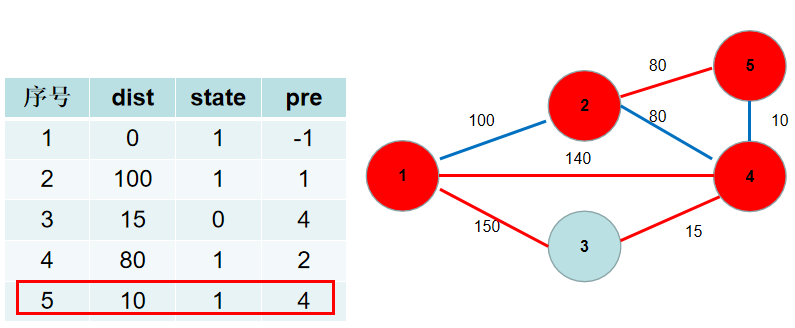
选
d
i
s
t
[
3
]
dist[3]
dist[3],没有可更新的。
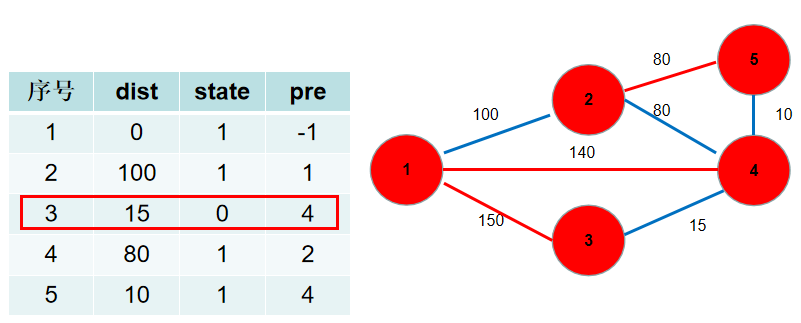
6.此时 d i s t dist dist 数组中保存了各个节点需要修的路长,加起来就是。 p r e pre pre 数组中保存了需要选择的边。
朴素Prim的代码实现
#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
#include<cstring>
using namespace std;
const int N = 510;
int g[N][N], dist[N];
bool st[N];
int n, m;
int Prim()
{
int res = 0;
memset(dist, 0x3f, sizeof dist); // 将所有节点的距离初始化为一个很大的值(无穷大)。
dist[1] = 0; // 从节点1开始算法。
for (int i = 0; i < n; ++i) // 遍历所有节点。
{
int t = -1;
// 找到还未加入集合的节点中距离最小的节点。
for (int j = 1; j <= n; ++j)
{
if (!st[j] && (t == -1 || dist[t] > dist[j]))
t = j;
}
st[t] = true; // 标记选中的节点为已访问。
// 如果最小距离仍保持初始值,说明有些节点是不可达的,图是非连通的。
if (dist[t] == 0x3f3f3f3f) return 0x3f3f3f3f;
// 累加记得提前,防止负权自环。
res += dist[t]; // 将当前节点的距离累加到结果中。
// 更新其他节点到集合的最小距离,如果有更小的距离则更新。
for (int j = 1; j <= n; ++j)
dist[j] = min(dist[j], g[t][j]);
}
return res; // 返回最小生成树的权值和。
}
int main()
{
cin.tie(0);
ios::sync_with_stdio(false);
memset(g, 0x3f, sizeof g); // 初始化所有边的权值为一个很大的值(无穷大)。
cin >> n >> m;
for (int i = 0; i < m; ++i)
{
int u, v, w;
cin >> u >> v >> w;
g[u][v] = g[v][u] = w; // 更新边的权值。
}
int t = Prim(); // 执行Prim算法得到最小生成树的权值和。
if (t == 0x3f3f3f3f) cout << "impossible" << endl; // 如果最小生成树不存在,则输出"impossible"。
else cout << t << endl; // 输出最小生成树的权值和。
return 0;
}
注意:
累加记得提前,防止负权自环。
- 与
Dijkstra可迭代 n − 1 n-1 n−1 次不同,Prim需要迭代 n n n 次。 - 最小生成树是针对无向图的,所以在读入边的时候,需要赋值两次。
- 要先累加再更新,避免 t t t 有自环,影响答案的正确性。后更新不会影响后面的结果么?不会的,因为 d i s t [ i ] dist[i] dist[i] 为 i i i 到集合 S S S 的距离,当 t t t 放入集合后,其 d i s t [ t ] dist[t] dist[t] 就已经没有意义了,再更新也不会影响答案的正确性。
- 需要特判一下第一次迭代,在我们没有做特殊处理时,第一次迭代中所有点到集合S的距离必然为无穷大,而且不会进行更新(也没有必要),所以不需要将这条边(第一次迭代时,找到的距离集合 S S S 最短的边)累加到答案中,也不能认定为图不连通。
- 如果需要设置起点为 i i i 的话,在初始化 d i s t dist dist 数组之后, d i s t [ i ] = 0 dist[i] = 0 dist[i]=0 即可,这样也可以省去每轮迭代中的两个 i f if if 判断。
附加:
带路径输出的Prim算法
#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
#include<cstring>
#include<vector>
#include<queue>
using namespace std;
const int N = 510;
int g[N][N], dist[N], pre[N];
bool st[N];
int n, m;
int Prim()
{
int res = 0;
memset(pre, -1, sizeof pre);
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
for (int i = 0; i < n; ++i)
{
int t = -1;
for (int j = 1; j <= n; ++j)
{
if (!st[j] && (t == -1 || dist[t] > dist[j]))
t = j;
}
st[t] = true;
if (dist[t] == 0x3f3f3f3f) return 0x3f3f3f3f;
res += dist[t];
for (int j = 1; j <= n; ++j)
{
if (dist[j] > g[t][j])
{
dist[j] = g[t][j];
pre[j] = t;
}
}
}
return res;
}
int main()
{
cin.tie(0);
ios::sync_with_stdio(false);
memset(g, 0x3f, sizeof g);
cin >> n >> m;
for (int i = 0; i < m; ++i)
{
int u, v, w;
cin >> u >> v >> w;
g[u][v] = g[v][u] = w;
}
int t = Prim();
if (t == 0x3f3f3f3f) cout << "impossible" << endl;
else cout << t << endl;
for (int i = 1; i <= n; ++i) cout << pre[i] << ' ';
cout << endl;
return 0;
}
堆优化Prim的代码实现
#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
#include<cstring>
#include<vector>
#include<queue>
using namespace std;
const int N = 510, M = 1e5 + 10;
typedef pair<int, int> PII;
bool st[N]; // 标记节点是否已经加入最小生成树
int n, m, dist[N]; // dist数组用于记录每个节点到最小生成树的距离
int h[N], e[M], ne[M], idx, w[M]; // 邻接表存储图的边信息
void add(int a, int b, int c)
{
e[idx] = b; // 存储边的另一个节点
w[idx] = c; // 存储边的权值
ne[idx] = h[a]; // 将边插入到节点a的邻接表头部
h[a] = idx++; // 更新节点a的邻接表头指针
}
int Prim()
{
int res = 0, cnt = 0; // res用于记录最小生成树的权值和,cnt用于记录已经选择的边数
priority_queue<PII, vector<PII>, greater<PII>> heap; // 最小堆,用于选择最短边
memset(dist, 0x3f, sizeof dist); // 初始化dist数组为无穷大
heap.push({ 0, 1 }); // 将节点1加入最小堆,距离为0
dist[1] = 0; // 节点1到最小生成树的距离为0
while (heap.size())
{
auto t = heap.top(); // 取出最小堆中距离最小的节点
heap.pop();
int ver = t.second, destination = t.first; // ver为节点,destination为距离
if (st[ver]) continue; // 如果节点已经在最小生成树中,跳过
st[ver] = true; // 将节点标记为已经加入最小生成树
res += destination; // 更新最小生成树的权值和
cnt++; // 增加已选择的边数
// 遍历节点ver的所有邻接边
for (int i = h[ver]; i != -1; i = ne[i])
{
auto u = e[i]; // 邻接边的另一个节点
if (dist[u] > w[i])
{
dist[u] = w[i]; // 更新节点u到最小生成树的距离
heap.push({ dist[u], u }); // 将节点u加入最小堆
}
}
}
// 如果最小生成树的边数小于n-1,则图不连通,返回0x3f3f3f3f表示不可达
if (cnt < n - 1) return 0x3f3f3f3f;
return res; // 返回最小生成树的权值和
}
int main()
{
cin.tie(0);
ios::sync_with_stdio(false);
memset(h, -1, sizeof h); // 初始化邻接表头指针为-1
cin >> n >> m; // 输入节点数和边数
for (int i = 0; i < m; ++i)
{
int a, b, c;
cin >> a >> b >> c;
add(a, b, c), add(b, a, c); // 添加无向图的边到邻接表中
}
int t = Prim(); // 计算最小生成树的权值和
if (t == 0x3f3f3f3f)
cout << "impossible" << endl; // 输出不可达
else
cout << t << endl; // 输出最小生成树的权值和
return 0;
}
Kruskal(克鲁斯卡尔)算法
Kruskal算法是计算无向连通加权图的最小生成树的经典贪心算法。
时间复杂度:
O
(
m
log
m
)
O(m \log m)
O(mlogm)
1.算法步骤
- 创建一个空的最小生成树 T T T。
- 将图中的所有边按权重从小到大排序。【 O ( m log m ) O(m \log m) O(mlogm) Kruskal算法时间复杂度的瓶颈】
- 从权重最小的边开始,如果当前边连接的两个节点不在 T T T 中,则将当前边加入 T T T,否则跳过当前边。【 O ( m ) O(m) O(m)】
- 重复步骤 3 3 3,直到T包含图中的所有节点为止。
- 最后得到的 T T T 即为该图的最小生成树。
2.算法运用
Kruskal算法求最小生成树
题目描述:
给定一个
n
n
n 个点
m
m
m 条边的无向图,图中可能存在重边和自环,边权可能为负数。
求最小生成树的树边权重之和,如果最小生成树不存在则输出 impossible。
给定一张边带权的无向图 G = ( V , E ) G=(V,E) G=(V,E),其中 V V V 表示图中点的集合, E E E 表示图中边的集合, n = ∣ V ∣ n=|V| n=∣V∣, m = ∣ E ∣ m=|E| m=∣E∣。
由 V V V 中的全部 n n n 个顶点和 E E E 中 n − 1 n−1 n−1 条边构成的无向连通子图被称为 G G G 的一棵生成树,其中边的权值之和最小的生成树被称为无向图 G G G 的最小生成树。
输入格式:
第一行包含两个整数
n
n
n 和
m
m
m。
接下来 m m m 行,每行包含三个整数 u , v , w u,v,w u,v,w,表示点 u u u 和点 v v v 之间存在一条权值为 w w w 的边。
输出格式:
共一行,若存在最小生成树,则输出一个整数,表示最小生成树的树边权重之和,如果最小生成树不存在则输出 impossible。
数据范围:
1
≤
n
≤
1
0
5
,
1
≤
m
≤
2
∗
1
0
5
1≤n≤10^5,1≤m≤2*10^5
1≤n≤105,1≤m≤2∗105,图中涉及边的边权的绝对值均不超过
1000
1000
1000。
输入样例:
4 5
1 2 1
1 3 2
1 4 3
2 3 2
3 4 4
输出样例:
6
代码实现:
#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
#include <algorithm>
#include<cstring>
using namespace std;
const int N = 1e5 + 10, M = 2e5 + 10, INF = 0x3f3f3f3f;
int n, m, p[N];
struct Edge
{
int a, b, w;
bool operator<(const Edge& rhs) const
{
return w < rhs.w;
}
} edges[M];
// 查找节点 x 的根节点(使用路径压缩优化)
int find(int x)
{
if (p[x] != x)
p[x] = find(p[x]);
return p[x];
}
// Kruskal 算法计算最小生成树的权值和
int kruskal()
{
// 按边权值从小到大排序
sort(edges, edges + m);
// 初始化每个节点的父节点为自身
for (int i = 1; i <= n; ++i)
p[i] = i;
int res = 0; // 最小生成树的权值和
int cnt = 0; // 已经选择的边数
// 遍历每条边
for (int i = 0; i < m; ++i)
{
int a = edges[i].a, b = edges[i].b, w = edges[i].w;
// 查找节点 a 和节点 b 所在的连通分量的根节点
a = find(a);
b = find(b);
if (a != b) // 如果 a 和 b 不在同一个连通分量中,即选择这条边
{
cnt++;
res += w; // 更新最小生成树的权值和
p[a] = b; // 将 a 所在的连通分量合并到 b 所在的连通分量中
}
}
// 如果最小生成树的边数小于 n - 1,则说明图不连通,返回 INF
if (cnt < n - 1)
return INF;
return res; // 返回最小生成树的权值和
}
int main()
{
cin.tie(0);
ios::sync_with_stdio(false);
cin >> n >> m; // 输入节点数和边数
for (int i = 0; i < m; ++i)
{
int a, b, w;
cin >> a >> b >> w;
edges[i] = {a, b, w}; // 保存边的信息
}
int t = kruskal(); // 计算最小生成树的权值和
if (t == INF)
cout << "impossible" << endl;
else
cout << t << endl; // 输出最小生成树的权值和
}