【二叉树】利用前序和中序遍历结果生成二叉树并输出其后序和层序遍历结果

news2024/10/6 4:12:01

🚀个人主页：为梦而生~ 关注我一起学习吧！
⭐️往期关于树的文章：
【哈夫曼树】基本概念、构建过程及C++代码
【线索二叉树】C++代码及线索化过程详解
欢迎阅读！

在这里插入图片描述

  1. 实验内容

根据二叉树先序和中序遍历的结果,生成该二叉树。并输出后序、层序遍历结果。

  1. 实验步骤
  • 结构体的定义：定义链表、队列、以及二叉树的结构体，方便算法的设计。
  • 输入数据：根据给定先序遍历和中序遍历结果，确定二叉树的根节点，并分别得到左右子树的先序遍历和中序遍历序列。
  • 树的创建：对于根节点左右子树分别递归地执行第1步得到子树，并将其连接到根节点上。
  • 重复第2步直到所有子树都生成，将所有的结点信息记录到数组中。
  • 根据所求得的二叉树以及数组中的信息，计算后序遍历的结果并输出。
  • 根据所求得的二叉树以及数组中的信息，利用队列的辅助，计算并输出层序遍历的结果。
  1. 详细设计

本设计使用的是广度优先搜索算法，并且需要输出路径，所以用到了栈和队列。详细设计方案如下：

  • 首先，定义二叉树、链表和队列结构体数据类型。
//定义树的存储结构 
typedef struct TreeNode {
    int val;
    struct TreeNode* left;
    struct TreeNode* right;
}*BiTree;
//定义链表的存储结构 
typedef struct Node {
	TreeNode* data;
	struct Node* next;
}Node, *QueueNode;
//定义队列的存储结构 
typedef struct Queue{
	Node* front, * rear;
}*LinkQueue;
  • 随后，定义空队以及辅助全局变量并初始化。
int pre[MAXSIZE], in[MAXSIZE], post[MAXSIZE]; // 定义全局数组，存放遍历结果
int idx[MAXSIZE];			// 记下每个节点在中序遍历结果中的下标位置
int leaves[MAXSIZE];		// 存放所有叶子节点

int post_idx = 0;			// 定义全局变量，记录后序遍历的当前位置
int leaf_idx = 0;			// 定义全局变量，记录叶子节点的个数
LinkQueue level_queue = (Queue*)malloc(sizeof(Queue));	//创建用于层序遍历的队列
  • 输入前序和中序遍历结果以及结点个数，用于二叉树的创建。
	int n;
    printf("请输入节点个数：");
    scanf("%d", &n);

    printf("请输入二叉树前序遍历结果：");
    for (int i = 0; i < n; i++) {
        scanf("%d", &pre[i]);
    }

    printf("请输入二叉树中序遍历结果：");
    for (int i = 0; i < n; i++) {
        scanf("%d", &in[i]);
        idx[in[i]] = i;
}
  • 根据给定的二叉树先序遍历和中序遍历结果构建二叉树，通过递归来实现对于左右子树的构建。首先根据当前前序遍历序列的第一个元素在中序遍历序列中找到对应的下标；根据找到的下标，可以得到当前元素的左右子树的前序和中序遍历序列范围；递归调用 buildTree 函数生成当前结点的左子树和右子树；在递归调用的过程中，每次都会基于当前的范围值不断更新相关索引值，直至生成完整棵二叉树。最后将生成的根结点指针返回，并完成二叉树的构建。
// 根据前序和中序遍历结果构建二叉树
BiTree buildTree(int pre_left, int pre_right, int in_left, int in_right) {
	//根据边界判断是否到叶子结点 
    if (pre_left > pre_right) {
        return NULL;
    }

    int root_val = pre[pre_left]; 	//结点的值为当前前序遍历当前的值 
    int in_idx = idx[root_val];		//找到中序遍历该结点对应的下标 

    TreeNode* root = createNode(root_val);	//创建新的结点 
    root->left = buildTree(pre_left + 1, pre_left + (in_idx - in_left), in_left, in_idx - 1);	//递归生成左子树 
    root->right = buildTree(pre_left + (in_idx - in_left) + 1, pre_right, in_idx + 1, in_right);//递归生成右子树 

    return root;	//返回根结点指针 
}
  • 递归遍历二叉树，输出后序遍历结果。采用递归算法实现，按照“左-子-根”的顺序访问每一个结点，并将其值存储到后序遍历结果数组 post 里。首先判断当前结点是否为空，若为空则直接返回；对于非空结点，先递归遍历其左子树，再递归遍历其右子树，以保证左右子树都已经访问完；最后，在左右子树均访问完毕之后，输出当前结点的值到后序遍历结果数组；将当前结点的值插入到后序遍历结果数组，这样最终我们就能得到符合要求的后序遍历结果。
// 递归遍历二叉树，生成后序遍历结果
void generate_postorder(BiTree root) {
    if (root == NULL) {
        return;
    }

    generate_postorder(root->left);	//递归遍历左字数 
    generate_postorder(root->right);//递归遍历右子树 
    post[post_idx++] = root->val;	//输出当前结点值 
}
  • 进行层序遍历并输出遍历结果。首先将二叉树的根节点入队，然后从队列中取出队头元素，并输出其值；若当前结点存在左子树，则将其左子节点入队；若当前结点存在右子树，则将其右子节点入队；继续对队列进行操作，直到队列为空。
void level_traversal(BiTree root, LinkQueue queue) {
	if (root == NULL) {
        return;
    }
	// 根结点入队
    enQueue(queue, root);
	// 队列不空时遍历
	while(queue->front != NULL){
		TreeNode* p = (TreeNode*)malloc(sizeof(TreeNode));
		deQueue(queue, &p);		// 出队
		printf("%d ", p->val);	// 输出
		
		if(root->left != NULL){
			enQueue(queue, p->left);	//若左子树不为空，将左子树根节点入队
		}			
		if(root->right != NULL){
			enQueue(queue, p->right);	//若右子树不为空，将右子树根节点入队
		}			
	} 
}
  1. 最终结果：
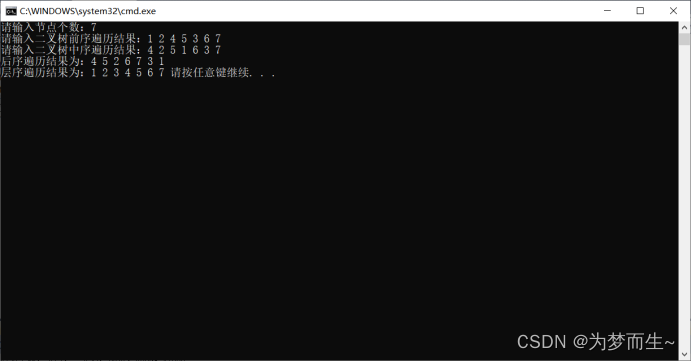
    在这里插入图片描述

代码实现：

#define _CRT_SECURE_NO_WARNINGS  //在VS中使用 避免出现scanf printf不安全的警告
#include <stdio.h>
#include <stdlib.h>

#define MAXSIZE 100	// 定义最大结点数量 

//定义树的存储结构 
typedef struct TreeNode {
    int val;
    struct TreeNode* left;
    struct TreeNode* right;
}*BiTree;
//定义链表的存储结构 
typedef struct Node {
	TreeNode* data;
	struct Node* next;
}Node, *QueueNode;
//定义队列的存储结构 
typedef struct Queue{
	Node* front, * rear;
}*LinkQueue;

int pre[MAXSIZE], in[MAXSIZE], post[MAXSIZE]; // 定义全局数组，存放遍历结果
int idx[MAXSIZE];			// 记下每个节点在中序遍历结果中的下标位置
int leaves[MAXSIZE];		// 存放所有叶子节点

int post_idx = 0;			// 定义全局变量，记录后序遍历的当前位置
int leaf_idx = 0;			// 定义全局变量，记录叶子节点的个数

// 创建新节点
BiTree createNode(int val) {
    TreeNode* newNode = (TreeNode*)malloc(sizeof(struct TreeNode));
    newNode->val = val;
    newNode->left = NULL;
    newNode->right = NULL;
    return newNode;
}

// 根据前序和中序遍历结果构建二叉树
BiTree buildTree(int pre_left, int pre_right, int in_left, int in_right) {
	//根据边界判断是否到叶子结点 
    if (pre_left > pre_right) {
        return NULL;
    }

    int root_val = pre[pre_left]; 	//结点的值为当前前序遍历当前的值 
    int in_idx = idx[root_val];		//找到中序遍历该结点对应的下标 

    TreeNode* root = createNode(root_val);	//创建新的结点 
    root->left = buildTree(pre_left + 1, pre_left + (in_idx - in_left), in_left, in_idx - 1);	//递归生成左子树 
    root->right = buildTree(pre_left + (in_idx - in_left) + 1, pre_right, in_idx + 1, in_right);//递归生成右子树 

    return root;	//返回根结点指针 
}

// 递归遍历二叉树，生成后序遍历结果
void generate_postorder(BiTree root) {
    if (root == NULL) {
        return;
    }

    generate_postorder(root->left);	//递归遍历左字数 
    generate_postorder(root->right);//递归遍历右子树 
    post[post_idx++] = root->val;	//输出当前结点值 
}

// 初始化队列
void initQueue(LinkQueue queue) {
    queue->front = NULL;
    queue->rear = NULL;
}

// 入队操作
void enQueue(LinkQueue queue, TreeNode* val) {
    QueueNode node = (QueueNode) malloc(sizeof(Node));
    node->data = val;
    node->next = NULL;

    if (queue->rear == NULL) {
        queue->front = node;
        queue->rear = node;
    } else {
        queue->rear->next = node;
        queue->rear = node;
    }
}

// 出队操作
void deQueue(LinkQueue queue, BiTree* val) {
    if (queue->front == NULL) {
        printf("Error: queue is empty!\n");
        exit(1);
    }

    *val = queue->front->data;
    QueueNode temp = queue->front;
    queue->front = queue->front->next;

    if (queue->front == NULL) {
        queue->rear = NULL;
    }

    free(temp);
}

// 层序遍历二叉树
void level_traversal(BiTree root, LinkQueue queue) {
	if (root == NULL) {
        return;
    }
	// 根结点入队
    enQueue(queue, root);
	// 队列不空时遍历
	while(queue->front != NULL){
		TreeNode* p = (TreeNode*)malloc(sizeof(TreeNode));
		deQueue(queue, &p);		// 出队
		printf("%d ", p->val);	// 输出
		
		if(root->left != NULL){
			enQueue(queue, p->left);	//若左子树不为空，将左子树根节点入队
		}			
		if(root->right != NULL){
			enQueue(queue, p->right);	//若右子树不为空，将右子树根节点入队
		}			
	} 
}

// 找出所有叶子节点
void find_leaves(BiTree root) {
    if (root == NULL) {
        return;
    }

    if (root->left == NULL && root->right == NULL) {
        leaves[leaf_idx++] = root->val;
    }

    find_leaves(root->left);
    find_leaves(root->right);
}

int main() {
	LinkQueue level_queue = (Queue*)malloc(sizeof(Queue));	//创建用于层序遍历的队列 
    int n;
    printf("请输入节点个数：");
    scanf("%d", &n);

    printf("请输入二叉树前序遍历结果：");
    for (int i = 0; i < n; i++) {
        scanf("%d", &pre[i]);
    }

    printf("请输入二叉树中序遍历结果：");
    for (int i = 0; i < n; i++) {
        scanf("%d", &in[i]);
        idx[in[i]] = i;
    }

    BiTree root = buildTree(0, n - 1, 0, n - 1);
    generate_postorder(root);
    find_leaves(root);

    printf("后序遍历结果为：");
    for (int i = 0; i < n; i++) {
        printf("%d ", post[i]);
    }
    printf("\n");

    printf("层序遍历结果为：");
    initQueue(level_queue);
    level_traversal(root, level_queue);
    printf("\n");

    printf("所有叶子节点为：");
    for (int i = 0; i < leaf_idx; i++) {
        printf("%d ", leaves[i]);
    }
    printf("\n");

    return 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/786866.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

pytest自动化测试框架tep环境变量、fixtures、用例三者之间的关系

pytest自动化测试框架tep环境变量、fixtures、用例三者之间的关系

tep是一款测试工具&#xff0c;在pytest测试框架基础上集成了第三方包&#xff0c;提供项目脚手架&#xff0c;帮助以写Python代码方式&#xff0c;快速实现自动化项目落地。 在tep项目中&#xff0c;自动化测试用例都是放到tests目录下的&#xff0c;每个.py文件相互独立&…
阅读更多...
低代码治好了CIO们的 “精神内耗”

低代码治好了CIO们的 “精神内耗”

目录 一、前言 二、低代码在企业数字化转型中能“C位出道”&#xff0c;凭什么&#xff1f; 三、低代码的数字化构建能力 四、结束语 一、前言 近两年&#xff0c;我发现身边的CIO/CTO朋友都得了一种“病”——“数字化焦虑”症。 他们经常皱着眉头问我&#xff1a;“老板对数字…
阅读更多...
gradio初体验

gradio初体验

背景 近期随着很多开源大模型的出现&#xff0c;对于其如何落地&#xff0c;或者说充分地去挖掘其实际应用领域和商业价值变得格外重要。于是乎&#xff0c;对于不懂技术的前方市场或销售人员&#xff0c;如何在没有形成AI产品之前向其展示算法模型效果呢&#xff1f;这时候gr…
阅读更多...
【严重】Citrix ADC 和 Citrix Gateway 远程代码执行漏洞（PoC）

【严重】Citrix ADC 和 Citrix Gateway 远程代码执行漏洞（PoC）

漏洞描述 Citrix ADC是应用程序交付和负载平衡解决方案&#xff0c;Citrix Gateway是一套安全的远程接入解决方案&#xff0c;常用于提供虚拟桌面和远程桌面服务&#xff0c;此外&#xff0c;Citrix ADC还被广泛用作Windows堡垒机。 在 Citrix ADC 和 Citrix Gateway 受影响版…
阅读更多...
《我为什么要听你的 如何与强势的人相处》读书笔记二

《我为什么要听你的 如何与强势的人相处》读书笔记二

目录 反驳例子 勇敢反击的益处 一些重要的自我保护法 不要再讲述你生活中的细节 别答应那些表意不明的请求 记录下一切 第一时间告知亲友 拒绝成为中间人 区别对待强势者 谨慎应对奉承话 想方设法快点跑 反驳例子 例子 例子&#xff1a; 例子&#xff1a; 例子&am…
阅读更多...
什么是UE像素流送，像素流推流是什么原理？

什么是UE像素流送，像素流推流是什么原理？

游戏开发者通常在运行游戏逻辑时会将游戏渲染到屏幕的同一台设备上来运行虚幻引擎应用&#xff0c;多人联网游戏可能会在应用程序的多个实例之间分发部分游戏逻辑&#xff0c;但每个单独的实例仍然会为自己的玩家在本地渲染游戏。即使是使用 HTML5 部署选项创建可以在 Web 浏览…
阅读更多...
CountDownLatch 一个神奇的计数器，您了解吗

CountDownLatch 一个神奇的计数器，您了解吗

一、CountDownLatch基础概念及案例 1.CountDownLatch是java.util.concurrent 包下提供一个同步工具类&#xff0c;它允许一个或多个线程一直等待&#xff0c;直到其他线程执行完成再执行。其本质就是一个计数器&#xff0c;传入一个初始的值&#xff0c;调用await 方法会阻塞当…
阅读更多...
vue+Element项目中v-for循环+表单验证

vue+Element项目中v-for循环+表单验证

如果在Form 表单里有通过v-for动态生成&#xff0c;如何设置验证呢&#xff1f; <el-form ref"ruleFormRef" :model"ruleForm" status-icon :rules"rules" label-width"120px"class"demo-ruleForm" hide-required-aster…
阅读更多...
大数据课程综合实验案例---课设问题汇总

大数据课程综合实验案例---课设问题汇总

最近翻看两年前的大数据课设&#xff0c;感觉这个大数据课设实验当时答辩 在大数据课设实验过程中&#xff0c;我遇到了很多问题&#xff0c;在这里做出汇总&#xff1a; 1、MySQL启动报错 首先&#xff0c;我的MySQL有时候启动不了&#xff0c;当我输入这个命令的时候&#…
阅读更多...
ModuleNotFoundError: No module named sklearn

ModuleNotFoundError: No module named sklearn

前言 出现ModuleNotFoundError: No module named sklearn’的debug过程记录 步骤 安装机器学习库&#xff0c;需要注意报错的sklearn是scikit-learn缩写。 pip install scikit-learn 完成&#xff0c;不再报错
阅读更多...
剖析Linuxptp中ptp4l实现--OC

剖析Linuxptp中ptp4l实现--OC

源码克隆地址&#xff1a; git://git.code.sf.net/p/linuxptp/code 项目官网文档&#xff1a; https://linuxptp.nwtime.org/documentation/ 关于linuxptp的相关配置可以参考以下博文&#xff1a; linuxptp/ptp4l PTP时钟同步配置选项 代码剖析 ptp4l的main函数在ptp4l.…
阅读更多...
“学习嵌入式开发：明确目标，提升技能“

“学习嵌入式开发：明确目标，提升技能“

嵌入式领域涵盖广泛&#xff0c;不可能一次性掌握所有知识。因此&#xff0c;明确学习目标和方向非常重要。选择感兴趣且与职业发展相关的领域进行深入学习是明智之举。 嵌入式技术在不断发展&#xff0c;过去与现在存在差异。选择学习当前行业的主流技术和趋势是明智选择。掌…
阅读更多...
基于STM32设计的人体健康监护系统(华为云IOT)

基于STM32设计的人体健康监护系统(华为云IOT)

一、设计需求 1.1 设计需求总结 根据需求，要求设计一款基于 STM32 的人体健康监护系统。采用系统模块化思路进行，将多个数模传感器收集到的数据和操作指令一并送至 STM32 中心处理器进行处理分析。 该系统可以实时监测被测者的心率、体温以及周围环境的温度，也同时可以通…
阅读更多...
生物信息学_玉泉路_课堂笔记_06 第六章 基因组学：遗传变异分析以及FGWAS

生物信息学_玉泉路_课堂笔记_06 第六章 基因组学：遗传变异分析以及FGWAS

&#x1f345; 课程&#xff1a;生物信息学_玉泉路_课堂笔记 中科院_2022秋季课 第一学期 &#x1f345; 个人笔记使用 &#x1f345; 2023/7/21 课程回顾 第六章 基因组学&#xff1a;遗传变异分析以及FGWAS 第一节 SNP 与 Indel 的鉴定与分析 基本概念 参考基因组 和基因组…
阅读更多...
tinkerCAD案例：9.Twist Earrings 扭耳环

tinkerCAD案例：9.Twist Earrings 扭耳环

tinkerCAD案例&#xff1a;9.Twist Earrings 扭耳环 In this lesson you learn how to create earrings by using cylinder shapes. Let’s get started! 在本课中&#xff0c;您将学习如何使用圆柱形制作耳环。让我们开始吧&#xff01; 说明 Drag a Cylinder shape to the w…
阅读更多...
为Android构建现代应用—— 练习状态管理

为Android构建现代应用—— 练习状态管理

介绍 本章是一个应用上一章&#xff1a;设计原则中学到的概念的项目。 项目的目标包括以下实现&#xff1a; • 创建一个应用程序&#xff0c;该应用程序使用View作为真实来源。 • 修改应用程序&#xff0c;使其使用ViewModel作为真实来源。 • 将状态和事件进行分组&#x…
阅读更多...
N型光伏电池技术“两头开花”，谁是诗和远方？

N型光伏电池技术“两头开花”，谁是诗和远方？

光伏产业已经进入大规模、市场化发展的新阶段。 近日&#xff0c;国家能源局公布了上半年全国电力工业统计数据&#xff0c;根据总装机容量&#xff0c;光伏装机已正式成为我国第二大电源装机&#xff0c;仅次于煤电。 作为新兴产业&#xff0c;光伏市场持续扩容总是伴随着技…
阅读更多...
SpringMVC----（1）基础

SpringMVC----（1）基础

SringMVC 1 SpringMVC简介2 SpringMVC入门案例2.1 入门案例2.2 入门案例工作流程2.3 bean加载控制2.4 PostMan工具 3 请求与响应3.1 请求映射路径3.2 Get和Post请求发送普通参数3.3 请求头的五种类型参数传递3.4 请求体的JSON数据传输参数3.5 日期型参数3.6 响应 4 REST风格4.1…
阅读更多...
SpringCloud整合Nacos配置中心

SpringCloud整合Nacos配置中心

&#x1f4dd; 学技术、更要掌握学习的方法&#xff0c;一起学习&#xff0c;让进步发生 &#x1f469;&#x1f3fb; 作者&#xff1a;一只IT攻城狮 &#xff0c;关注我&#xff0c;不迷路 。 &#x1f490;学习建议&#xff1a;1、养成习惯&#xff0c;学习java的任何一个技术…
阅读更多...
NoSQL之Redis配置使用

NoSQL之Redis配置使用

目录 一、关系数据库与非关系型数据库 1.1.关系型数据库的概述 1.2关系型数据库的优缺点 1.2.1优点 1.2.2缺点 1.3.非关系型数据库的概述 二.关系数据库与非关系型数据库的区别 2.1数据存储方式不同 2.2扩展方式不同 2.3对事务性的支持不同 2.4非关系型数据库产生背景 2…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023