题目
判断给定的链表中是否有环。如果有环则返回true,否则返回false。
数据范围:链表长度 0≤n≤10000,链表中任意节点的值满足 ∣val∣<=100000
要求:空间复杂度 O(1),时间复杂度 O(n)
输入分为两部分,第一部分为链表,第二部分代表是否有环,然后将组成的head头结点传入到函数里面。-1代表无环,其它的数字代表有环,这些参数解释仅仅是为了方便读者自测调试。实际在编程时读入的是链表的头节点。
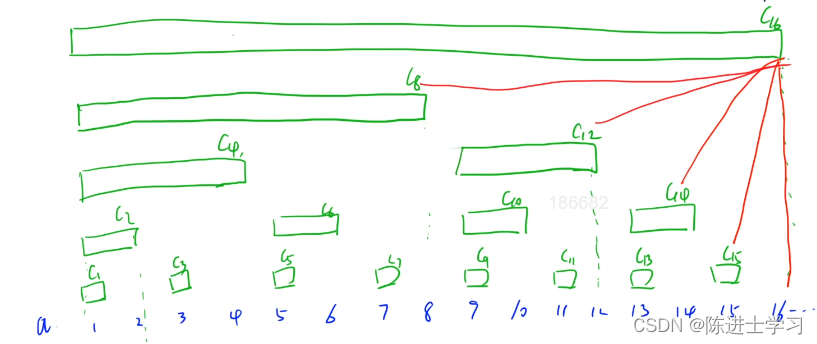
例如输入{3,2,0,-4},1时,对应的链表结构如下图所示:
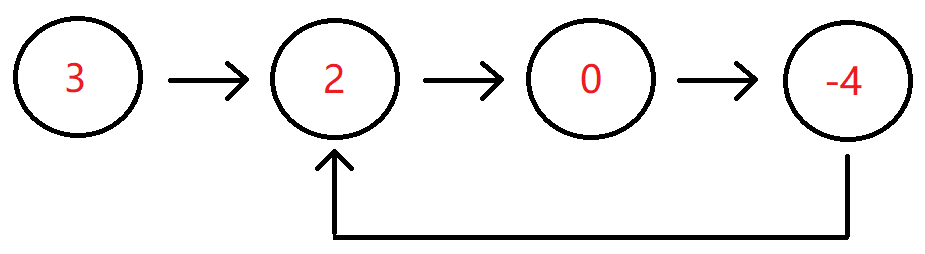
可以看出环的入口结点为从头结点开始的第1个结点(注:头结点为第0个结点),所以输出true。
示例1
输入:
{3,2,0,-4},1
返回值:
true
说明:
第一部分{3,2,0,-4}代表一个链表,第二部分的1表示,-4到位置1(注:头结点为位置0),即-4->2存在一个链接,组成传入的head为一个带环的链表,返回true
示例2
输入:
{1},-1
返回值:
false
说明:
第一部分{1}代表一个链表,-1代表无环,组成传入head为一个无环的单链表,返回false
示例3
输入:
{-1,-7,7,-4,19,6,-9,-5,-2,-5},6
返回值:
true
思路1
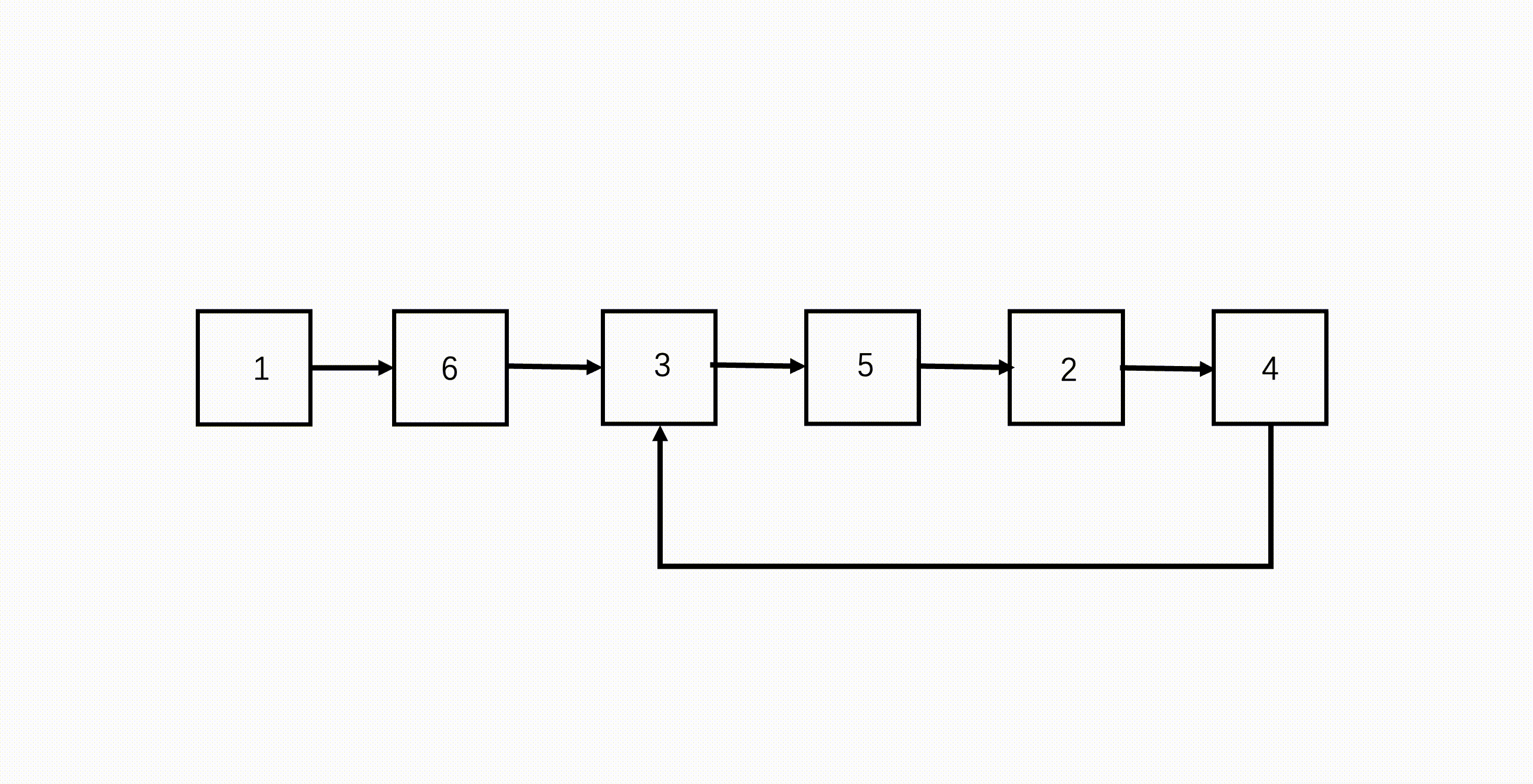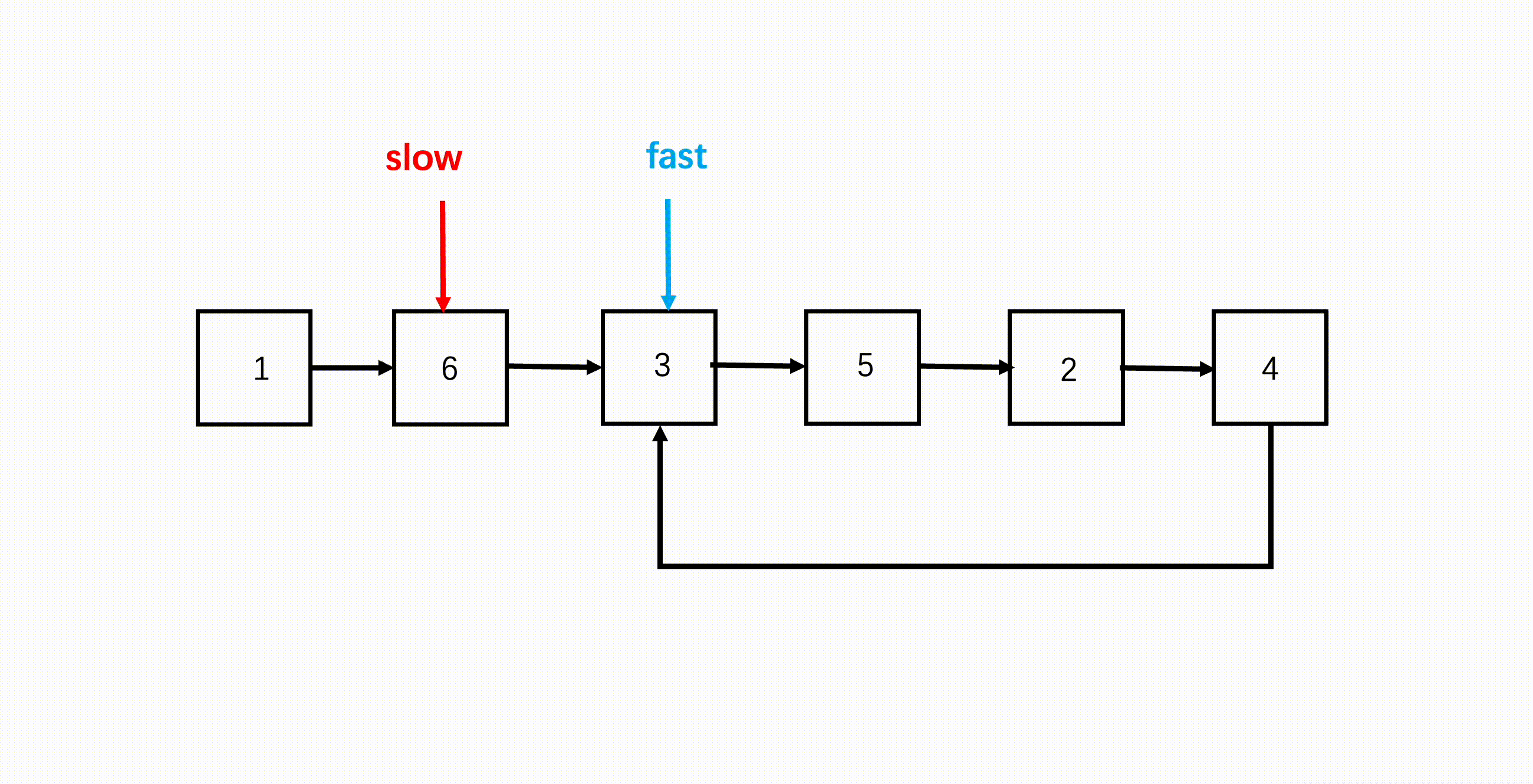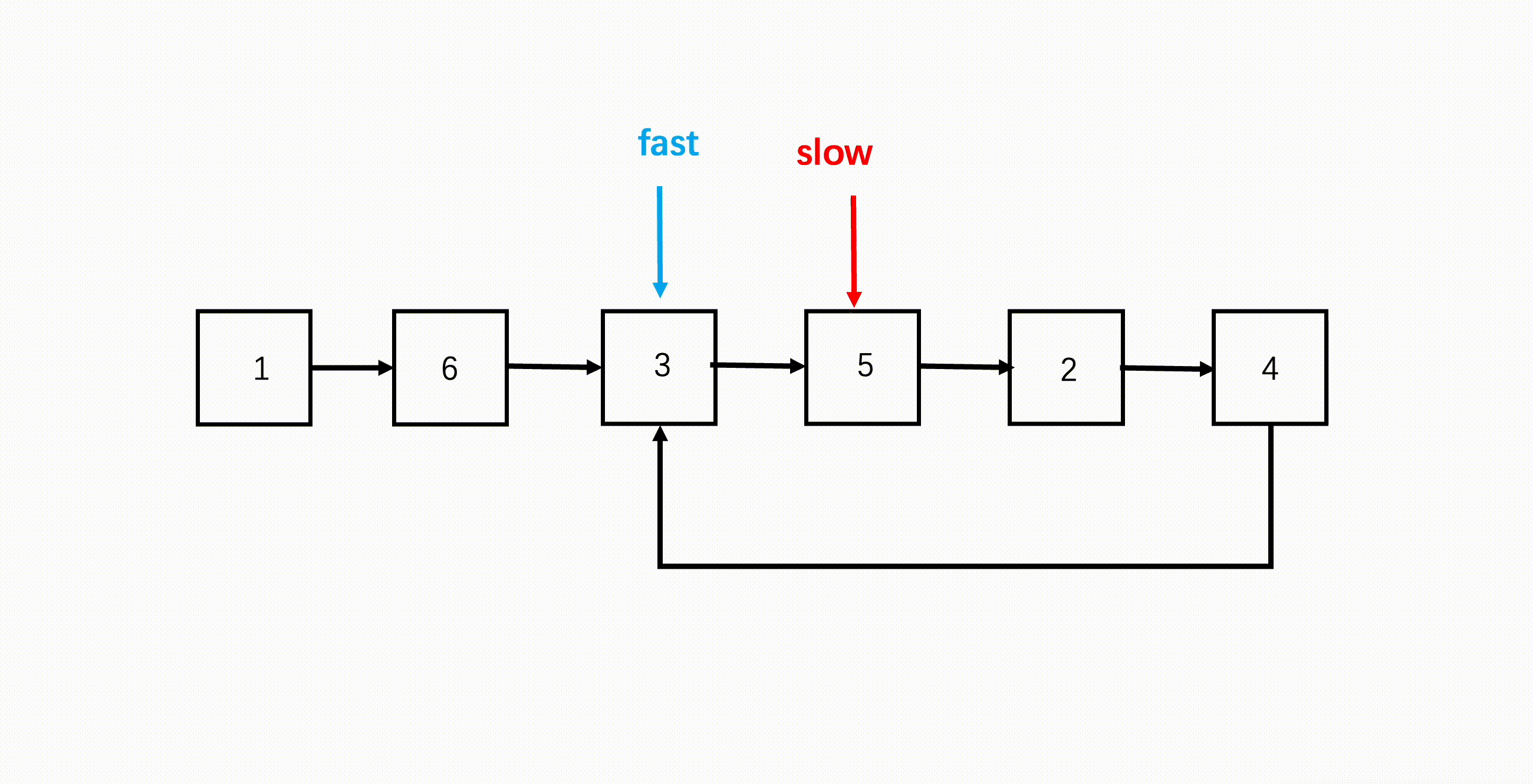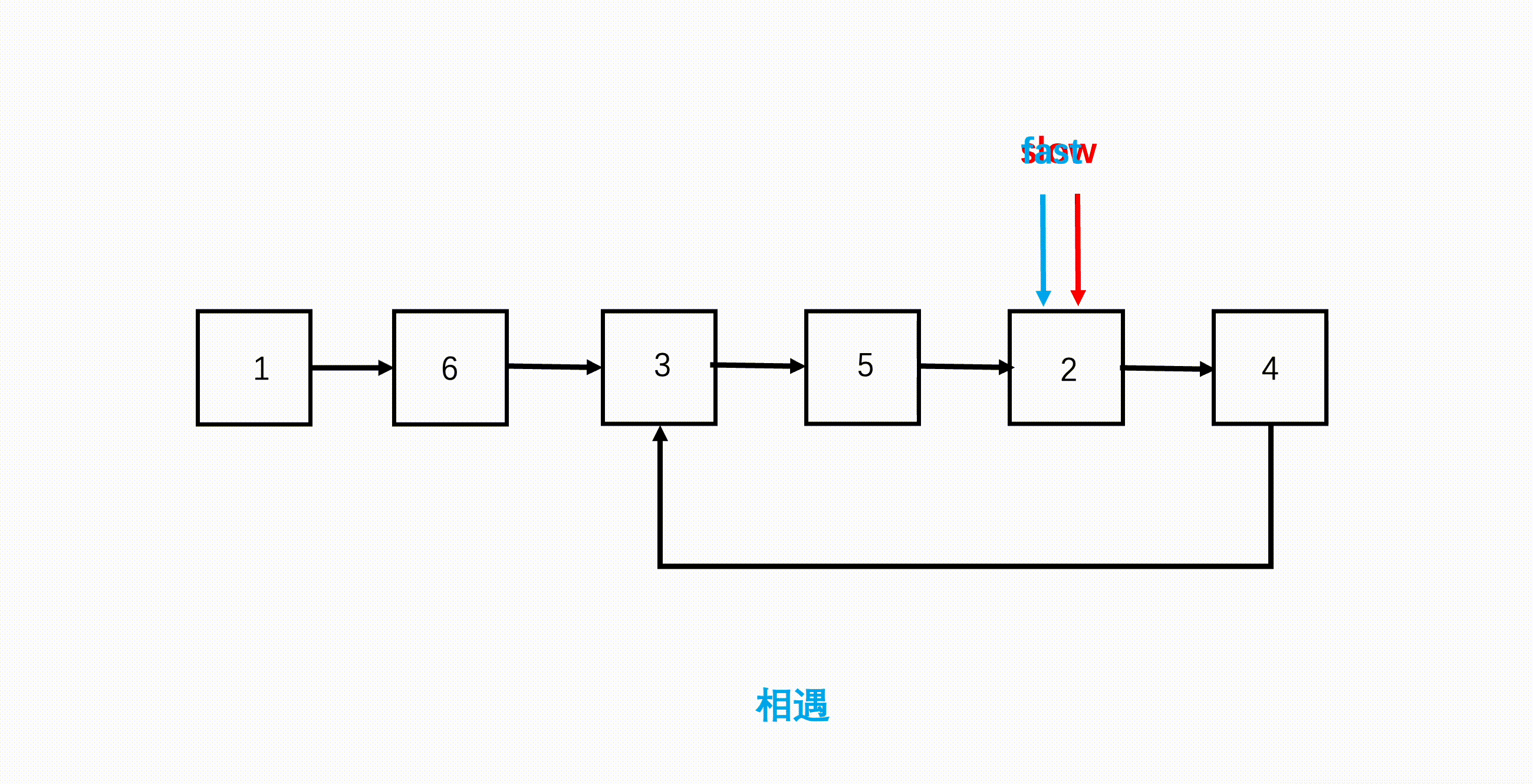
使用两个指针,fast 与 slow。
它们起始都位于链表的头部。随后,slow 指针每次向后移动一个位置,而fast 指针向后移动两个位置。如果链表中存在环,则 fast 指针最终将再次与 slow 指针在环中相遇。
知识点:双指针
双指针指的是在遍历对象的过程中,不是普通的使用单个指针进行访问,而是使用两个指针(特殊情况甚至可以多个),两个指针或是同方向访问两个链表、或是同方向访问一个链表(快慢指针)、或是相反方向扫描(对撞指针),从而达到我们需要的目的。
解答代码1
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
bool hasCycle(ListNode *head) {
if (head == nullptr) {
return false;
}
// 定义快慢指针
auto slow = head;
auto fast = head;
// 循环退出条件为快指针先到链表尾部
while (fast != nullptr && fast->next != nullptr) {
slow = slow->next;
fast = fast->next->next;
if (slow == fast) {
// 快慢指针相遇表示有环
return true;
}
}
return false;
}
};
思路2
遍历链表中的每个节点,并将它记录下来;一旦遇到了此前遍历过的节点,就可以判定链表中存在环,需借助哈希表(C++中std::unordered_set)。
但这种解法的空间复杂度为O(N),其中 N 为链表中节点的数目。因为需要将链表中的每个节点都保存在哈希表当中。
解答代码2
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
#include <unordered_set>
class Solution {
public:
bool hasCycle(ListNode *head) {
if (head == nullptr) {
return false;
}
auto cur = head;
std::unordered_set<ListNode *> sets;
while (cur != nullptr) {
if (sets.find(cur) != sets.end()) {
// 在unordered_set中找到了,表示有环
return true;
} else
sets.emplace(cur);
cur = cur->next;
}
return false;
}
};