数组、前缀和、树状数组的区别：

        数组：修改某点O（1），求区间O（n）

        前缀和：修改某点O（n），求区间O（1）

        树状数组：修改某点O（logn），求区间O（logn）

树状数组采取折中的方式，降低整体的时间复杂度。

由于算法复杂度取决于最坏的情况的复杂度，所以当数据量很大的时候，树状数组比单独的数组或者前缀和快。

---

基于二进制

C[x] 为以 x 结尾的，2^k 个单位长度的总和（k为x右侧 0 的个数）

例，x = 8（1000），则 k 为 3，C[x] 为2^3 = 8 个单位长度的总和

---

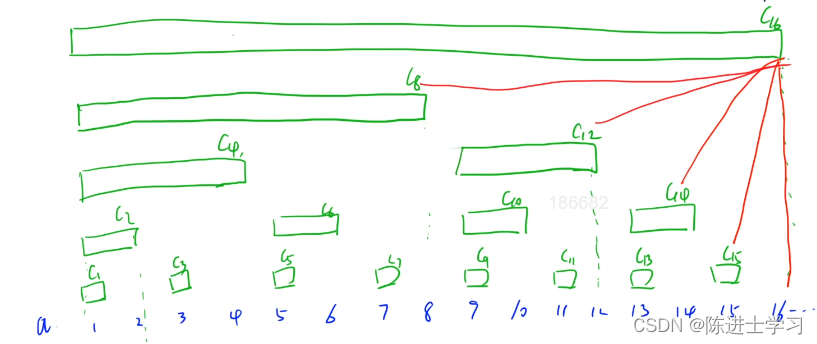
lowbit函数：求某二进制从右侧往左侧数，第一个1及其后面的0组成的数

int lowbit(int x){
    return x&(-x);
}

 修改某点

int add(int x,int k){	//x为修改的点，k为增加或减少的值 
	for(int i=x;i<=n;i+=lowbit(i)) a[i]+=k;
}

 查询区间 [a,b] 的和

int sum(int x,int y){
	int ans=0;
	for(int i=y;i;i-=lowbit(i)) ans+=a[i];
	for(int i=x-1;i;i-=lowbit(i)) ans-=a[i];
	return ans;
}