A - Weird FunctionA - Weird Function
题目大意
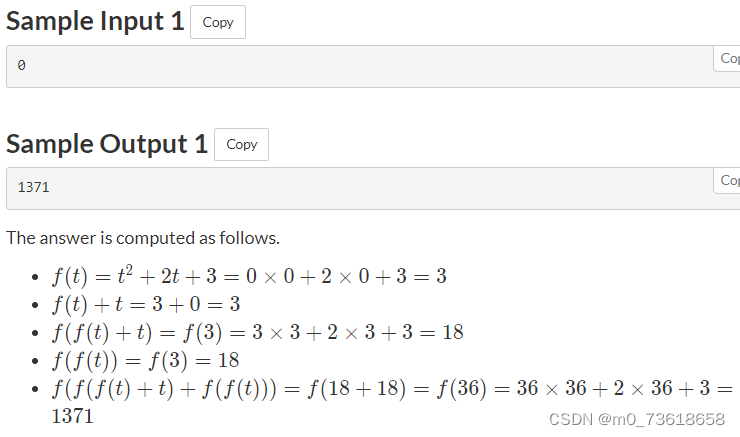
要求计算 f(f(f(t)+t)+f(f(t))) ,其中 t 是一个给定的整数。
- 函数 f(x) 定义为 f(x) = x^2 + 2x + 3。
思路分析
定义实现函数 f(int t),并嵌套调用。
时间复杂度
O(1)
AC代码
#include<bits/stdc++.h>
using namespace std;
int f(int t) {
int res = t * t + 2 * t + 3;
return res;
}
int main() {
int t;
cin >> t; =
int ans = f(f(f(t) + t) + f(f(t)));
cout << ans << endl;
return 0;
}
B - Longest SegmentB - Longest Segment
题目大意
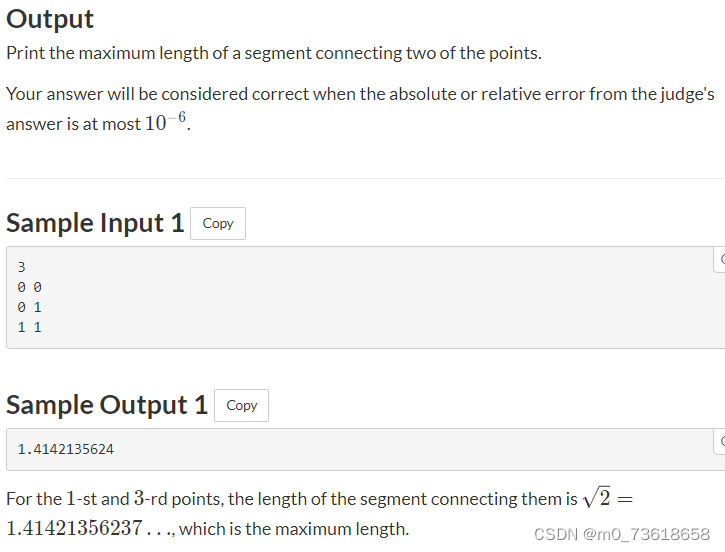
题目要求在二维平面上找到N个点中连接两个点的最大长度。
思路分析
因为数据范围较小所以可以暴力枚举。注意要满足题目要求误差。在C++中,输出小数时,小数部分的数字位数可能不够满足误差容忍度的要求。所以需要使用 std::fixed 和 std::setprecision(10) 来确保输出的小数位数达到10位,以满足题目对精度的要求。
时间复杂度
O(N2)
AC代码
#include<bits/stdc++.h>
using namespace std;
int main(){
int N;
cin >> N;
vector<int> x(N), y(N);
for(int i=0; i<N; i++) {
cin >> x[i] >> y[i];
}
double ans = 0;
for(int i=0; i<N; i++){
for(int j=i+1; j<N; j++){
int X = x[i]-x[j], Y = y[i]-y[j];
ans = max(ans, sqrt(X*X+Y*Y));
}
}
cout << fixed << setprecision(10) << ans << endl;
return 0;
}
C - Happy New Year! C - Happy New Year!
题目大意
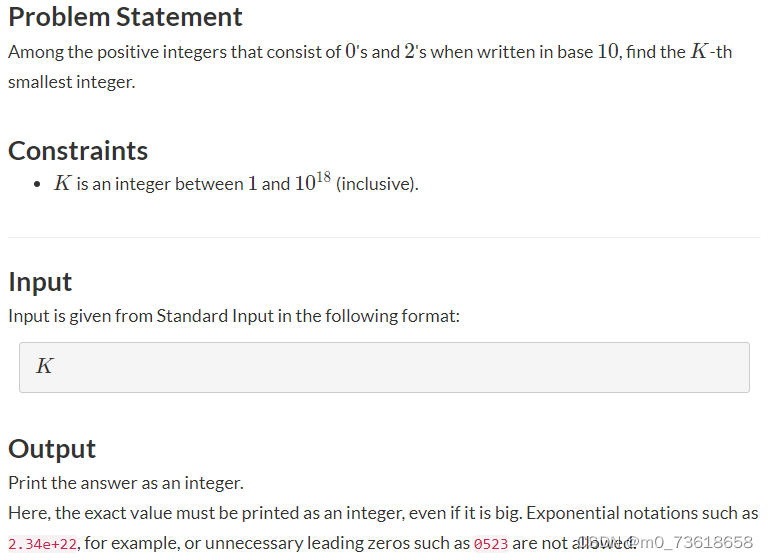
在由0和2组成的十进制数中,找到第K个最小的整数。
思路分析
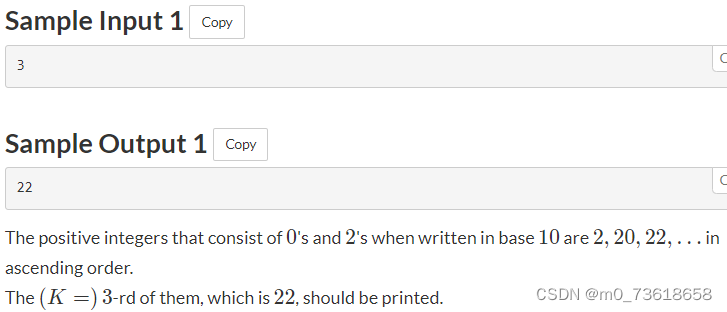
由0和2组成的正整数在十进制下只包含0和2两个数字。可以将这些整数转换为二进制表示。
实际上,满足条件的第K个最小整数就是K的二进制表示,其中将1替换为2。
时间复杂度
O(log(K))
AC代码
#include<bits/stdc++.h>
using namespace std;
string convert(long long x){
string res;
while(x>0){
res.push_back('0'+(x%2)); // 将每一位数字转换为0或1并添加到结果字符串中
x/=2;
}
reverse(res.begin(),res.end()); // 反转字符串,得到正确的二进制表示
return res;
}
void output(string s){
for(auto &nx : s){
if(nx=='1'){cout << '2';} // 将1替换为2
else{cout << '0';} // 保持0不变
}
cout << '\n';
}
int main(){
long long k;
cin >> k;
output(convert(k)); // 调用函数进行转换和输出
return 0;
}