Contest Duration: 2023-07-22(Sat) 20:00 - 2023-07-22(Sat) 21:40 (local time) (100 minutes)
头文件和宏
#include<iostream>
#include<string>
#include<vector>
using namespace std;
#define int long long
#define fer(i,a,b) for(int i=a;i<b;i++)
#define cf int T;cin>>T;while(T--)
#define pb push_back
#define IOS ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
以下只附主代码
A First ABC
从头开始,找出ABC三个字母都至少出现一次的最小长度
signed main(){
IOS;
int n;cin>>n;
string s;cin>>s;
bool fa=0,fb=0,fc=0;
int cnt=0;
fer(i,0,n){
if(s[i]=='A')fa=1;
else if(s[i]=='B')fb=1;
else if(s[i]=='C')fc=1;
if(fa&&fb&&fc){
cnt=i;break;
}
}
cout<<cnt+1;
return 0;
}
B Vacation Together
找出n人均有空闲的最大天数
signed main(){
IOS;
int n,d;cin>>n>>d;
bool f[d]={0};
string s;
fer(i,0,n){
cin>>s;
fer(j,0,d){
if(s[j]=='x')f[j]=1;
}
}
int cnt=0,mx=0;
fer(i,0,d){
if(f[i]==0){
cnt++;
mx=max(mx,cnt);
}else cnt=0;
}
cout<<mx;
return 0;
}
C Find it!
有向图,N个结点,N条边,一个结点只会指向另外一个结点,产生一条边。题目要求输出任意环。
这种方式形成的有向图一定有环,最小的环是M=2,最大的环是M=N,所以只要顺着找N+1次,必然会出现环,res里最后一个结点必然在环里。即使重复在一个环里循环也无妨,只需从后向前截取这个环作为结果。
const int N=2e5+5,mod=1e9+7;
int a[N];
signed main(){
IOS;
int n;cin>>n;
fer(i,1,n+1)cin>>a[i];
vector<int>res;res.clear();
int j=1;
res.pb(j);
fer(i,0,n+1){
res.pb(a[j]);
j=a[j];
}
int k;
for(int i=n-1;i>=0;i--){
if(res[i]==res[n]){
k=i;break;
}
}
cout<<n-k<<endl;
for(int i=k;i<n;i++){
cout<<res[i]<<" ";
}
return 0;
}
D Grid Ice Floor
滑冰,如果玩过类似的4399小游戏会感到熟悉。
在冰面上只能朝指定方向滑行,直到遇到障碍物停下,中途不能改变方向。问最多能滑过多少块冰。问题在于:如何判定停止递归?不能只是单纯遇到走过的点就停止。比如下图中的红线是可以走的,但如果“遇到走过的点就停止”,那么就不会递归这条红线的情况,这是错误的。
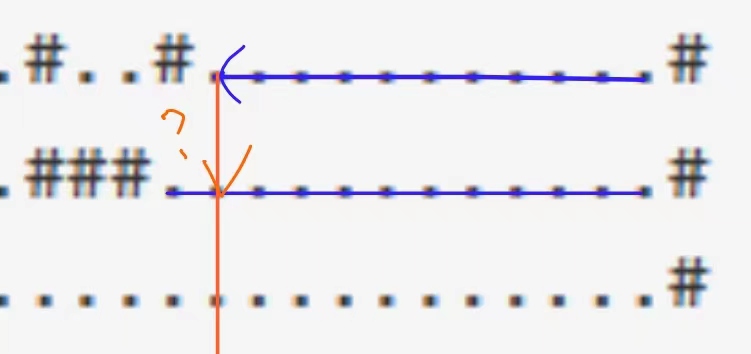
因此我设置了两个布尔数组,f代表走过的点,用来计数;f2代表该点是否作为过停留的结点向四个方向递归,如果f2==1,那么我们不必重复去递归
int a[202][202];bool f[202][202],f2[202][202];
int cnt=0;
void solve(int x,int y,int op){//1上 2下 3左 4右
if(f[x][y]==0){
cnt++;f[x][y]=1;
}
if(op==0&&f2[x][y]==0){
f2[x][y]=1;
if(a[x-1][y])solve(x-1,y,1);
if(a[x+1][y])solve(x+1,y,2);
if(a[x][y-1])solve(x,y-1,3);
if(a[x][y+1])solve(x,y+1,4);
return;
}else if(op==1){
if(a[x-1][y])solve(x-1,y,1);
else solve(x,y,0);
}else if(op==2){
if(a[x+1][y])solve(x+1,y,2);
else solve(x,y,0);
}else if(op==3){
if(a[x][y-1])solve(x,y-1,3);
else solve(x,y,0);
}else if(op==4){
if(a[x][y+1])solve(x,y+1,4);
else solve(x,y,0);
}
}
signed main(){
IOS;
int n,m;cin>>n>>m;
string s;
fer(i,0,n){
cin>>s;
fer(j,0,m){
if(s[j]=='.')a[i+1][j+1]=1;
}
}
solve(2,2,0);
cout<<cnt<<endl;
// fer(i,1,n+1){
// fer(j,1,m+1)cout<<f[i][j]<<" ";
// cout<<endl;
// }
return 0;
}
下面是非递归的版本,用的是队列,这种方式开销较小
vector<int> dx = {1, 0, -1, 0};
vector<int> dy = {0, 1, 0, -1};
int main(){
int N, M;
cin >> N >> M;
vector<string> S(N);
for (int i = 0; i < N; i++){
cin >> S[i];
}
vector<vector<bool>> used(N, vector<bool>(M, false));
used[1][1] = true;
vector<vector<bool>> used2(N, vector<bool>(M, false));
used2[1][1] = true;
queue<pair<int, int>> Q;
Q.push(make_pair(1, 1));
while (!Q.empty()){
int x = Q.front().first;
int y = Q.front().second;
Q.pop();
for (int i = 0; i < 4; i++){
int x2 = x, y2 = y;
while (S[x2 + dx[i]][y2 + dy[i]] == '.'){
x2 += dx[i];
y2 += dy[i];
used2[x2][y2] = true;
}
if (!used[x2][y2]){
used[x2][y2] = true;
Q.push(make_pair(x2, y2));
}
}
}
int ans = 0;
for (int i = 0; i < N; i++){
for (int j = 0; j < M; j++){
if (used2[i][j]){
ans++;
}
}
}
cout << ans << endl;
for (int i = 0; i < N; i++){
for (int j = 0; j < M; j++){
cout<<used2[i][j]<<" ";
}
cout<<endl;
}
return 0;
}
参考:Submission #43834581
E Defect-free Squares
问无洞正方形有多少个。动态规划
dp初始化为最大值3000+
- 如果该点是洞,该点dp[i][j]=0;
- 如果不是:
- 如果是最底下一行和最右面一列,dp[i][i]=1
- 如果不是:dp[i][i]=min(dp ,dp[i+1][j]+1,dp[i][j+1]+1,dp[i+1][j+1]+1),也就是取(自身、右面+1、下面+1、右下+1)中的最小值。
如果右面或者下面是洞,都影响自身构建无洞正方形
bool f[3001][3001];
int dp[3001][3001];
signed main(){
IOS;
int h,w,n;cin>>h>>w>>n;
int a,b;
fer(i,1,n+1){
cin>>a>>b;
f[a][b]=1;
}
fer(i,1,h+1){
fer(j,1,w+1)dp[i][j]=3005;
}
int sum=0;
for(int i=h;i>=1;i--){
for(int j=w;j>=1;j--){
if(i==h||j==w)dp[i][j]=1;
if(i<h)dp[i][j]=min(dp[i][j],dp[i+1][j]+1);
if(j<w)dp[i][j]=min(dp[i][j],dp[i][j+1]+1);
if(i<h&&j<w)dp[i][j]=min(dp[i][j],dp[i+1][j+1]+1);
if(f[i][j])dp[i][j]=0;
sum+=dp[i][j];
}
}
cout<<sum<<endl;
return 0;
}
参考:Submission #43837221
F Yet Another Grid Task
给一个网格,有黑块有白块。小明要把白块涂成黑块使得网格变beautiful,beautiful的定义如下:一个黑块的下面一块和右下角的一块也是黑块。问有多少种涂法。
动态规划,dp初始化为1,按列dp,对每列找到黑块出现的最早一次位置,在这位置之后的块的可能次数均为0(因为黑块之下必须是黑块,已经被定好了),在这位置之前的块,可能次数是自身的可能次数+下方块的可能次数,然后dp整体下移
const int N=2e5+1,mod=998244353;
signed main(){
IOS;
int n,m;cin>>n>>m;
vector<string>s(n);
fer(i,0,n)cin>>s[i];
vector<int> dp(n+1,1);
fer(i,0,m){
int x=0;
while(x<n&&s[x][i]=='.')x++;
for(int j=x+1;j<=n;j++){
dp[j]=0;
}
for(int j=n-1;j>=0;j--){
dp[j]+=dp[j+1];
dp[j]%=mod;
}
for(int j=n;j>0;j--){
dp[j]=dp[j-1];
dp[j]%=mod;
}
}
cout<<dp[0];
return 0;
}
参考:Submission #43851107
G One More Grid Task
在网格内拉一个矩形,求(矩形内和x矩形内最小值)的最大值
s存放该列数字的和,t存放该列数字的最小值,待想
signed main(){
IOS;
int n,m;cin>>n>>m;
vector<vector<int> > a(n,vector<int>(m));
fer(i,0,n){
fer(j,0,m)cin>>a[i][j];
}
int ans=0;
fer(u,0,n){
vector<int>s(m),t(m,1e9);
fer(d,u,n){
fer(i,0,m){
s[i]+=a[d][i];
t[i]=min(a[d][i],t[i]);
}
vector<int> l(m,-1),r(m,m),stk;
fer(i,0,m){
while(!stk.empty()&&t[i]<t[stk.back()]){
r[stk.back()]=i;
stk.pop_back();
}
if(!stk.empty())l[i]=stk.back();
stk.pb(i);
}
vector<int> pre(m+1);
fer(i,0,m)pre[i+1]=pre[i]+s[i];
fer(i,0,m)ans=max(ans,t[i]*(pre[r[i]]-pre[l[i]+1]));
}
}
cout<<ans;
return 0;
}
参考:Submission #43853592