数据结构与算法之排序算法
- 1 使用递归的方式求最大值
- 2 时间复杂度
- 3 选择排序和冒泡排序的时间复杂度分析
- 4 插入排序时间复杂度分析 (O(N^2))
- 5 二分法的详解与扩展
- 6 对数器
- 7 归并排序
- 8 归并排序的应用
- 9 逆序对问题
- 10 归并排序非递归方式
- 11 快速排序
- 12 堆排序
- 13 桶排序
1 使用递归的方式求最大值
public class GetMaxTest {
public static int getMax(int[] arr){
return process(arr,0,arr.length);
}
// arr[L..R]范围上的最大值
public static int process(int[] arr,int L,int R){
// arr[L..R]范围上只有一个数 直接返回 base case
if (L == R) {
return arr[L];
}
// 中点
// 如果采用这种写法
// int mid = (L + R) / 2
// 存在的问题是 如果 L 和 R 比较大的时候可能会出现溢出的情况
int mid = L + ((R - L) >> 1);
int leftMax = process(arr,L,mid);
int rightMax = process(arr,mid + 1 ,R);
return Math.max(leftMax,rightMax);// 时间复杂度 O(1)
}
public static void main(String[] args) {
int[] arr = {10,20,35,6,8};
System.out.println(getMax(arr));
}
}
递归将整个函数的调用过程 调用过程
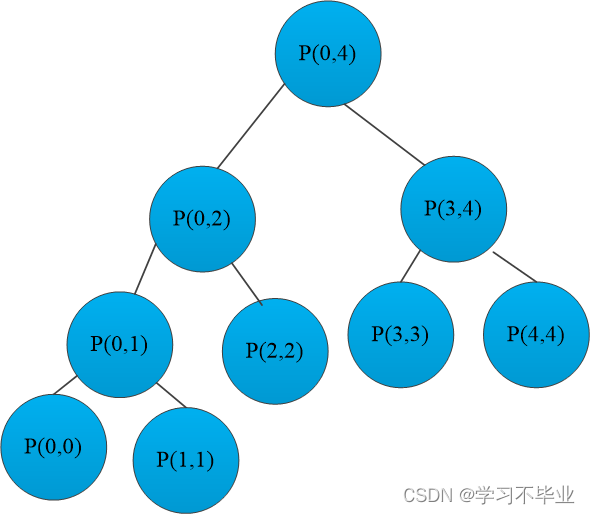
类似二叉树的后续遍历
递归行为和递归行为时间复杂度的估算
master公式 :
T(N) = a * T (N/b) + O(N^d)
T(N) : 母问题的规模
a : 调用次数
b : 子问题的规模
O(N^d): 除了子问题之外的时间复杂度
在此问题中T(N)公式为 :
a = 2 b = 2 d=0
T(N) = 2 * T(N/2) + O(1)
中间加一个打印 额外的时间复杂度就变成了 O(N)
log(b,a) > d 复杂度为O(N^log(b,a))
log(b,a) = d 复杂度为O(N^d*logN)
log(b,a) < d 复杂度为O(N^d)
此递归的时间复杂度为O(N)
2 时间复杂度
- 常数时间的操作
一个操作如果和样本的数据量没有关系,每次都是固定时间内完成的操作,叫做常数操作
时间复杂度作为一个算法流程中,常数操作数量的一个指标,常用O来表示,具体来说,需要对一个算法的流程非常熟悉,然后去写这个算法的流程中,发生了多少常数操作,从而总结出常数操作数量的表达式,
在表达式中,只要高阶项,不要低阶项,也不要高阶项的系数,剩下的部分如果为f(N)那么时间复杂度为O(f(N))
评价一个算法流程的好坏,先看时间复杂度指标,然后再分析不同样本下的实际运行时间,也就是"常数项时间"
3 选择排序和冒泡排序的时间复杂度分析
选择排序
coding
public class SelectionSortTest {
public static void selectionSort(int[] arr){
if (arr == null || arr.length < 2){
return;
}
// 保证 i - N-1 上的数最小
for (int i = 0; i < arr.length - 1 ; i++) {
int minIndex = i;
// 在 i - (N - 1)上找最小值的下标
for (int j = i + 1; j < arr.length;j++){
minIndex = arr[j] < arr[minIndex] ? j : minIndex;
}
// 可能会出现 i == index
swap(arr,i,minIndex);
}
}
public static void swap(int[] arr,int i,int j){
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
// 使用下面这种交换方法 i 和 j 不能相等
/* arr[i] = arr[i] ^ arr[j];
arr[j] = arr[i] ^ arr[j];
arr[i] = arr[i] ^ arr[j];*/
}
}
冒泡排序
coding
public class BubbleSortTest {
public static void bubbleSort(int[] arr){
if (arr == null || arr.length < 2){
return;
}
// 0 - (N - 1) 范围上相邻两个数交换 放在最后 时间复杂度为 O(N^2)
for (int e = arr.length - 1; e > 0; e--){
// 从0开始,前一个数比后一个数大 就交换
for (int j = 0;j < e;j++){
if (arr[j] > arr[j + 1]){
swap(arr,j,j+1);
}
}
}
}
// 可以交换的前提是 i != j 否则会将值修改成 0
public static void swap(int[] arr,int i,int j){
arr[i] = arr[i] ^ arr[j];
arr[j] = arr[i] ^ arr[j];
arr[i] = arr[i] ^ arr[j];
}
}
异或运算
相同为0,不同为1
异或运算的性质
0 ^ N = N
N ^ N = 0
异或运算满足交换律和结合律
a ^ b ^ c = a ^ c ^ b
异或运算可以理解为无进位相加
交换两个数使用异或的方法
// 自己跟自己异或是 0
// 自己跟 0 异或是自己
// 交换的前提是在内存中是两块不同的区域
int a = 10;
int b = 20;
a = a ^ b;
b = a ^ b;// a^b^b a^0 a
a = a ^ b; // a = a ^ a ^ b 0 ^ b b
关于异或运算的算法
1 已知在一个数组中,只有一个数出现了奇数次,其它数都出了偶数次,如何找到这个数
coding
public static int findOccurOddTimes1(int[] arr) {
int eor = 0;
for (int ele : arr) {
eor ^= ele;
}
return eor;
}
2 一个数组中,有两个数字出现了奇数次 这两个数字不相同 其他数都是出现了偶数次 如何找出这两个数字
/**
* 一个数组中,有两个数字出现了奇数次 这两个数字不相同 其他数都是出现了偶数次 如何找出这两个数字
*/
public static int[] findOccurOddTimes2(int[] arr) {
int[] retArr = new int[2];
int eor = 0;
for (int i = 0; i < arr.length; ++i) {
eor ^= arr[i];
}
// eor 就是 a ^ b 因为 a和 b 不相等 所以 eor一定不是0 一定有一位是1
// a 和 b 一定有一位上 a 是 0 b 是 1 所有的这些数可以分成这一位上是0和这一位上不是 0
// 提取出数据最右边的 1 一个数字 与 它按位取反+1 就会提取出最右侧的1
int rightNumber = eor & (~eor + 1);
int onlyOne = 0;
for (int cur : arr) {
// 数组中所有这一位上是0的数与 onlyOne作与运算 最终得到的结果就是 A或B中的其中一个
if ((cur & rightNumber) == 0) {
onlyOne ^= cur;
}
}
retArr[0] = onlyOne;
retArr[1] = onlyOne ^ eor;
return retArr;
}
leecode类似题目
一个整型数组里除了两个数字只出现一次,其他的数字都出现了两次。请写程序找出这两个只
出现一次的数字。
数据范围:数组长度 ,数组中每个数的大小 要求:空间复杂度 ,时间复杂度 提示:输出时按非降序排列。
提示:输出时按非降序排列。
import java.util.*;
public class Solution {
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param nums int整型一维数组
* @return int整型一维数组
*/
public int[] FindNumsAppearOnce (int[] nums) {
// write code here
if (nums == null || nums.length < 2){
return null;
}
int eor = 0;
for (int i = 0;i < nums.length;++i){
eor ^= nums[i];
}
int rightNumber = eor & (~eor + 1);
int onlyOne = 0;
for(int i= 0;i < nums.length;++i){
if((nums[i] & rightNumber) == 0){
onlyOne ^= nums[i];
}
}
int otherOne = (eor ^ onlyOne);
int maxValue = onlyOne > otherOne ? onlyOne : otherOne;
int minValue = onlyOne > otherOne ? otherOne : onlyOne;
return new int[]{minValue,maxValue};
}
}
4 插入排序时间复杂度分析 (O(N^2))
coding
插入排序在某些数据状况下,时间复杂度比选择排序和冒泡排序要好
从0开始 依次保证从 0 - (N -1)范围上有序
public class InsertSortTest {
public static void insertSort(int[] arr){
if (arr == null || arr.length < 2){
return;
}
// 0 - 0有序
// 0 - i有序
for (int i = 1; i < arr.length ; i++) {
// j 位置的数 比 j + 1 位置上的数大 就交换
for (int j = i - 1; j >= 0 && arr[j] > arr[j + 1]; j--) {
swap(arr,j,j + 1);
}
}
}
public static void swap(int[] arr,int i,int j){
arr[i] = arr[i] ^ arr[j];
arr[j] = arr[i] ^ arr[j];
arr[i] = arr[i] ^ arr[j];
}
}
5 二分法的详解与扩展
1 在一个有序数组中找某个数是否存在
public class BinarySearchTest {
public static void main(String[] args) {
int[] arr = {9,12,14,17,28,35,49};
System.out.println(isExists(arr,14));
}
// 二分查找
public static boolean isExists(int[] arr,int num){
if (arr == null || arr.length == 0){
return false;
}
int L = 0;
int R = arr.length - 1;
// 第一个位置和最后一个位置就是 直接返回
if (arr[L] == num || arr[R] == num){
return true;
}
// 不是 才开始二分查找
while ( L < R) {
int mid = L + ((R -L) >> 1);
if (arr[mid] < num){
// 往右半查找
L = mid + 1;
} else if (arr[mid] > num){
//往左半查找
R = mid - 1;
} else {
return true;
}
}
return arr[L] == num;
}
}
2 在一个数组中,找一个数最左侧的位置 同样可以使用二分法查找
/**
* 在一个有序数组中,找>=某个数最左侧的位置
* @param arr
* @param X
* @return
*/
public static int searchLeftValue(int[] arr,int X){
if (arr == null || arr.length == 0){
return -1;
}
int L = 0;
int R = arr.length - 1;
int index = -1;
while ( L < R){
int mid = L + ((R - L) >> 1);
if (arr[mid] < X) { // 小于的时候就是往右找
L = mid + 1;
} else if (arr[mid] >= X){ // 打到中间位置 往左找
index = mid;
R = mid - 1;
}
}
return index;
}
leetcode题目
请实现无重复数字的升序数组的二分查找
给定一个 元素升序的、无重复数字的整型数组 nums 和一个目标值 target ,
写一个函数搜索 nums 中的 target,如果目标值存在返回下标(下标从 0 开始),否则返回 -1
import java.util.*;
public class Solution {
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param nums int整型一维数组
* @param target int整型
* @return int整型
*/
public int search (int[] nums, int target) {
// write code here
if(nums == null || nums.length == 0){
return -1;
}
if(nums[0] == target){
return 0;
}
if(nums[nums.length - 1] == target){
return nums.length - 1;
}
int index = -1;
int leftIndex = 0;
int rightIndex = nums.length - 1;
while(leftIndex < rightIndex){
int mid = leftIndex + ((rightIndex - leftIndex) >> 1);
if(nums[mid] < target){
leftIndex = mid + 1;
} else if (nums[mid] > target) {
rightIndex = mid - 1;
} else {
return mid;
}
}
if(nums[leftIndex] == target){
index = leftIndex;
}
return index;
}
}
3 在一个有序数组中,找<= 某个数最右侧的位置
coding
/**
* 在一个有序数组中,找<= 某个数最右侧的位置
* @param arr
* @param X
* @return
*/
public static int getRightValue(int[] arr,int X){
if (arr == null || arr.length == 0){
return -1;
}
int L = 0;
int R = arr.length - 1;
int index = -1;
while (L < R) {
int M = L + ((R - L) >> 1);
// 中间位置的数小于等于X 往右继续找
if (arr[M] <= X) {
index = M;
L = M + 1;
} else{
R = M - 1;
}
}
return index;
}
4 局部最小问题 (数组无序,相邻的两个数一定不相等)
coding
/**
* 局部最小值问题:
* 无序数组,任意两个相邻的数不等,找到存在局部最小的位置
* 0位置比1位置小,则0位置是局部最小,n-2位置比n-1位置小,返回n-1位置
* 中间位置i,需满足 i 比左边小也比右边小,则i位置是局部最小
* 局部最小位置存在即可返回,不用返回所有的位置
* @param arr
* @return
*/
public static int getLessIndex(int[] arr){
if (arr == null || arr.length == 0){
return -1;
}
if (arr.length == 1 || arr[0] < arr[1]){
return 0;
}
if (arr[arr.length -1 ] < arr[arr.length -2 ]){
return arr.length -1 ;
}
int L = 1;
int R = arr.length - 2;
while (L < R){
int M = L + ((R - L) >> 1);
// 中点位置的数比后一个数要大 往右查找
if (arr[M] > arr[M+1]){
L = M + 1;
} else if (arr[M] > arr[M-1]){ // 中点位置的数比前一个数要大 往左查找
R = M -1;
} else { // 中点位置的数小于前一个 也小于后一个 直接返回
return M;
}
}
return L;
}
leetcode 类似题目
给定一个长度为n的数组nums,请你找到峰值并返回其索引。数组可能包含多个峰值,
在这种情况下,返回任何一个所在位置即可。
1.峰值元素是指其值严格大于左右相邻值的元素。严格大于即不能有等于
2.假设 nums[-1] = nums[n] = -∞
3.对于所有有效的 i 都有 nums[i] != nums[i + 1]
4.你可以使用O(logN)的时间复杂度实现此问题吗?
coding
import java.util.*;
public class Solution {
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
* 此问题实际上是局部最大问题
* @param nums int整型一维数组
* @return int整型
*/
public int findPeakElement (int[] nums) {
// write code here
if(nums == null || nums.length == 0){
return -1;
}
if(nums.length == 1 || nums[0] > nums[1]){
return 0;
}
if(nums[nums.length - 1] > nums[nums.length - 2]){
return nums.length -1;
}
int L = 1;
int R = nums.length - 2;
while(L < R){
int M = L + ((R - L) >> 1);
// 当前数比后一个要小 往右半查找
if(nums[M] < nums[M + 1]){
L = M + 1;
// 中间的数比前一个数大 则往左半查找
} else if (nums[M] < nums[M - 1] ){
R = M - 1;
// 中间的数比后一个大且比前一个大 则当前数就是最大的
} else {
return M;
}
}
return L;
}
}
6 对数器
对数器的概念和使用
- 有一个你想要测试的方法A
- 实现复杂度不好但是容易实现的方法
- 实现一个随机样本产生器
- 把方法a和方法b跑相同的随机样本
- 如果有一个随机样本使得比对结果不一致,打印样本进行人工干预,改对方法A或者方法B
- 当样本量很多时比对测试依然正确,可以确定方法A已经正确
coding
public static void test1() {
int testTime = 5000000;
boolean isSucceed = true;
long startTime = System.currentTimeMillis();
for (int i = 0; i < testTime; ++i) {
int[] arr = genRandArr(100, 100);
int[] cpyArr = copyArray(arr);
Arrays.sort(cpyArr);
selectSort(arr);
if (!isEqual(arr, cpyArr)) {
isSucceed = false;
break;
}
}
long endTimes = System.currentTimeMillis();
System.out.println((endTimes - startTime));
System.out.println(isSucceed ? "success" : "failed");
}
// 生成随机数
// Math.random() 返回 [0-1)之间的小数
public static int[] genRandArr(int maxSize, int maxValue) {
// 0 <= Math.random() < 1.0
int[] arr = new int[(int) ((maxSize + 1) * Math.random())];
for (int i = 0; i < arr.length; ++i) {
arr[i] = (int) ((maxValue + 1) * Math.random() - (maxValue + 1) * Math.random());
}
return arr;
}
public static int[] copyArray(int[] srcArr) {
int[] destArr = new int[srcArr.length];
System.arraycopy(srcArr, 0, destArr, 0, srcArr.length);
return destArr;
}
public static boolean isEqual(int[] arr1, int[] arr2) {
if (arr1.length != arr2.length) return false;
for (int i = 0; i < arr1.length; i++) {
if (arr1[i] != arr2[i]) return false;
}
return true;
}
/**
* 选择排序
* 每次选择出最小的数放在指定的位置
* @param arr
*/
public static void selectSort(int[] arr) {
for (int i = 0; i < arr.length - 1; i++) {
for (int j = i + 1; j < arr.length; j++) {
if (arr[j] < arr[i]) {
swap(arr, i, j);
}
}
}
}
7 归并排序
整体就是一个简单递归,左边排好序、右边排好序、让其整体有序
让其整体有序的过程里用了外排序方法
public static void mergeSort(int arr[]){
if (arr == null || arr.length < 2){
return;
}
processSort(arr,0,arr.length-1);
}
public static void processSort(int[] arr,int L,int R){
if (R == L){
return;
}
int M = L + ((R-L) >> 1);
// 先让左边有序
processSort(arr,L,M);
// 再让右边有序
processSort(arr,M+1,R);
// 最后合并
merge(arr,L,M,R);
}
// 将左边和右边合并 合并过程的时间复杂度是O(N)
public static void merge(int[] arr,int L,int M,int R){
// 创建一个数组 拷贝数据
int[] tempArr = new int[R - L + 1];
// 临时数组索引
int index = 0;
// 指向左边数组的下标
int p1 = L;
// 指向右边有序数组的下标
int p2 = M+1;
// 两边都不越界
while(p1 <= M && p2 <= R) {
tempArr[index++] = arr[p1] <= arr[p2] ? arr[p1++] : arr[p2++];
}
// 左边不越界
while(p1 <= M){
tempArr[index++] = arr[p1++];
}
// 右边不越界
while (p2 <= R){
tempArr[index++] = arr[p2++];
}
// 将排好序的数据拷贝到原数组中
for (int i = 0;i<tempArr.length;++i){
arr[L+i] = tempArr[i];
}
}
8 归并排序的应用
求小和问题
小和问题和逆序对问题
小和问题
在一个数组中,每一个数左边比当前数小的数累加起来,叫做这个数组
的小和。求一个数组 的小和。
例子:[1,3,4,2,5]
1左边比1小的数,没有;
3左边比3小的数,1;
4左边比4小的数,1、3;
2左边比2小的数,1;
5左边比5小的数,1、3、4、2;
所以小和为1+1+3+1+1+3+4+2=16
小和问题可以转换成右侧有几个数比它大
时间复杂度为 O(N^2)
// 时间复杂度 O(N^2)
public static int vioMethod(int[] arr){
int ret = 0;
for (int i = 1;i < arr.length;++i){
for(int j = 0;j < i;++j){
if (arr[j] < arr[i]){
ret+=arr[j];
}
}
}
return ret;
}
使用归并排序改写
// 既要排好序 又要求小和
public static int smallSum(int[] arr){
if (arr == null || arr.length < 2) {
return 0;
}
return process(arr,0,arr.length-1);
}
public static int process(int[] arr,int L,int R){
if (L == R){
return 0;
}
int mid = L + ((R-L) >>1);
// 返回左边合并之前的小和 + 右边合并之前的小和 + 两边合并之后的小和
return process(arr,L,mid) + process(arr,mid + 1,R) + smallMerge(arr,L,mid,R);
}
public static int smallMerge(int[] arr,int L,int M,int R){
int[] tempArr = new int[R - L + 1];
int index = 0;
int p1 = L;
int p2 = M + 1;
int ret = 0;
while(p1 <= M && p2 <= R){
// 相等的时候 右组先拷贝 并且不产生小和
ret += arr[p1] < arr[p2] ? (R - p2 +1) * arr[p1] : 0;
// 谁小拷贝谁
tempArr[index++] = arr[p1] < arr[p2] ? arr[p1++] : arr[p2++];
}
while (p1 <= M){
tempArr[index++] = arr[p1++];
}
while (p2 <= R){
tempArr[index++] = arr[p2++];
}
for(int i = 0;i < tempArr.length;++i){
arr[L + i] = tempArr[i];
}
return ret;
}
9 逆序对问题
逆序对问题 在一个数组中,左边的数如果比右边的数大,则这两个数
构成一个逆序对,请打印所有逆序对,求出逆序对的个数
public static class InversePair {
private int maxVal;
private int minVal;
public InversePair () {}
public InversePair(int maxVal, int minVal) {
this.maxVal = maxVal;
this.minVal = minVal;
}
public int getMaxVal() {
return maxVal;
}
public void setMaxVal(int maxVal) {
this.maxVal = maxVal;
}
public int getMinVal() {
return minVal;
}
public void setMinVal(int minVal) {
this.minVal = minVal;
}
@Override
public String toString() {
return "InversePair{" +
"maxVal=" + maxVal +
", minVal=" + minVal +
'}';
}
@Override
public boolean equals(Object o) {
if (this == o) return true;
if (o == null || getClass() != o.getClass()) return false;
InversePair that = (InversePair) o;
return maxVal == that.maxVal &&
minVal == that.minVal;
}
@Override
public int hashCode() {
return Objects.hash(maxVal, minVal);
}
}
private static List<InversePair> inversePairs = new ArrayList<>();
public static void main(String[] args) {
int[] arr = {8,7,6,5,4,3,2,1};
System.out.println(getReverseOrderCnt(arr));
for (InversePair pair : inversePairs) {
System.out.println(pair);
}
}
public static int getReverseOrderCnt(int[] arr){
if (arr == null || arr.length < 2){
return 0;
}
return process(arr,0,arr.length - 1);
}
public static int process(int[] arr,int L,int R) {
if (L == R) {
return 0;
}
int M = L + ((R -L) >> 1);
return process(arr,L,M) + process(arr,M+1,R) + merge(arr,L,M,R);
}
public static int merge(int[] arr,int L,int M,int R){
int[] tempArr = new int[R - L + 1];
int p1 = L;
int p2 = M + 1;
int index = 0;
int ret = 0;
// 这里一定是有一边是拷贝完成的
while (p1 <= M && p2 <= R){
// 升序排列 谁大拷贝谁
ret += arr[p1] > arr[p2] ? (R - p2 + 1) : 0;
if (arr[p1] > arr[p2]){
int tempIndex = p2;
while (tempIndex <= R){
inversePairs.add(new InversePair(arr[p1],arr[tempIndex++]));
}
}
tempArr[index++] = arr[p1] > arr[p2] ? arr[p1++] : arr[p2++];
}
while (p1 <= M) {
tempArr[index++] = arr[p1++];
}
while (p2 <= R){
tempArr[index ++] = arr[p2++];
}
for (int i = 0; i < tempArr.length ; i++) {
arr[L + i] = tempArr[i];
}
return ret;
}
10 归并排序非递归方式
public class MergeSortNoRecursionTest {
public static void main(String[] args) {
int[] arr = {10,7,6,2,10,3,90,23,12};
mergeSortNoRecursion(arr);
System.out.println(Arrays.toString(arr));
}
public static void mergeSortNoRecursion(int arr[]){
if (arr == null || arr.length < 2){
return;
}
int N = arr.length;
// 步长
int mergeSize = 1;
while (mergeSize < N){
// 当前左组的第一个位置
int L = 0;
// 左组的位置不能越界
while (L < N){
// 中间位置
int M = L + mergeSize - 1;
// 不够退出
if (M >= N){
break;
}
// 右组的位置如果够 会来到 M + mergeSize 越界右组的位置就是 N -1
int R = Math.min(M + mergeSize,N - 1 );
merge(arr,L,M,R);
// 左组的位置取到上一次右组位置的下一个位置
L = R + 1;
}
// 防止溢出
if (mergeSize > N /2){
break;
}
// 步长乘2
mergeSize <<= 1;
}
}
public static void merge(int[] arr,int L,int M,int R){
int[] tempArr = new int[R - L + 1];
int index = 0;
int p1 = L;
int p2 = M + 1;
while (p1 <= M && p2 <= R){
tempArr[index++] = arr[p1] <= arr[p2] ? arr[p1 ++] : arr[p2 ++];
}
while (p1 <= M){
tempArr[index ++] = arr[p1 ++];
}
while (p2 <= R){
tempArr[index ++] = arr[p2 ++];
}
for (int i = 0 ; i < tempArr.length;i++){
arr[L + i] = tempArr[i];
}
}
}
11 快速排序
首先来看如下问题
荷兰国旗问题
问题1 : 给定一个数组arr,和一个数num,请把小于等于num的数放在数组的左边,大于num的数放在数组的右边。要求额外空间复杂度O(1),时间复杂度O(N)
解决步骤 :
划分小于的区域 一开始在最左边
遍历数组,如果当前值不超过num,则和小于等于区域的下一个数作交换,小于等于区域往右扩,如果当前数大于num,则直接遍历下一个,直到遍历完成结束
小于等于区域一直在推着等于区域往右走
package com.chao.test;
import java.util.Arrays;
/**
* @author Mrchao
* @version 1.0.0
* @date 2023-07-22
*/
public class NetherlandsFlagTest {
public static void main(String[] args) {
int[] arr = {9,5,10,4,4,6,7,7,8,10,7,10};
partition(arr,0,arr.length - 1,7);
System.out.println(Arrays.toString(arr));
}
public static void swap(int[] arr,int a,int b){
int temp = arr[a];
arr[a] = arr[b];
arr[b] = temp;
}
/**
* 给定一个数组arr,和一个数num,请把小于num的数放在数组的左边,
* 等于num的数放在数组的中间,大于num的数放在数组的右边。
* 要求额外空间复杂度O(1),时间复杂度O(N)
* @param arr
* @param l 数组的左边界
* @param r 数组的右边界
* @param p 比较的数
*/
public static void partition(int[] arr,int l,int r,int p) {
// 小于区域的左边界
int less = l - 1;
// 大于区域右边界
int more = r + 1;
while (l < more){
// 当前数小于给定的数 当前数和小于区域的下一个做交换 l继续往后走
if (arr[l] <= p){
swap(arr,l++,++less);
} else { // 当前数大于给定的数 和大于区域的前一个数做交换 l不动
swap(arr,l,--more);
}
}
}
}
问题 2
给定一个数组arr,和一个数num,请把小于num的数放在数组的左边,等于num的数放在数组的中间,大于num的数放在数组的右边。要求额外空间复杂度O(1),时间复杂度O(N)
处理步骤 :
划分小于区域的右边界 划分大于区域的左边界
遍历数组
- arr[i] < num [i]和 小于区域的下一个作交换, 小于区域往右扩,i++
- arr[i] == num 继续遍历 i ++
- arr[i] > num arr[i]和大于区域的前一个作交换 ,大于区域左扩,i原地不动
package com.chao.test;
import java.util.Arrays;
/**
* @author Mrchao
* @version 1.0.0
* @date 2023-07-22
*/
public class NetherlandsFlagTest {
public static void main(String[] args) {
int[] arr = {9,5,10,4,4,6,7,7,8,10,7,10};
partition(arr,0,arr.length - 1,7);
System.out.println(Arrays.toString(arr));
}
public static void swap(int[] arr,int a,int b){
int temp = arr[a];
arr[a] = arr[b];
arr[b] = temp;
}
/**
* 给定一个数组arr,和一个数num,请把小于num的数放在数组的左边,
* 等于num的数放在数组的中间,大于num的数放在数组的右边。
* 要求额外空间复杂度O(1),时间复杂度O(N)
* @param arr
* @param l 数组的左边界
* @param r 数组的右边界
* @param p 比较的数
*/
public static void partition(int[] arr,int l,int r,int p) {
// 小于区域的左边界
int less = l - 1;
// 大于区域右边界
int more = r + 1;
while (l < more){
// 当前数小于给定的数 当前数和小于区域的下一个做交换 l继续往后走
if (arr[l] < p){
swap(arr,l++,++less);
//当前数大于给定的数 和大于区域的前一个数做交换 l不动
} else if (arr[l] > p){
swap(arr,l,--more);
} else { // 直接下一个
l ++;
}
}
}
}
快排第一个版本
选数组中的最后一个数作划分值,将小于等于此划分值的数都放在数组的左边,然后将划分值和数组小于区域的下一个值做交换,则此划分值左边都是小于等于此划分值的,此值右侧都是大于此划分值的,然后让左侧和右侧递归重复此过程,最终会让整个数组都有序
public static void swap(int[] arr,int a,int b){
int temp = arr[a];
arr[a] = arr[b];
arr[b] = temp;
}
public static void quickSort(int[] arr){
if (arr == null || arr.length < 2){
return;
}
process(arr,0,arr.length - 1);
}
public static void process(int[] arr,int L,int R){
if (L >= R) {
return;
}
int lessIndex = partition(arr, L, R);
process(arr,L,lessIndex);
process(arr,lessIndex + 2,R);
}
public static int partition(int[] arr,int L,int R){
int pivot = arr[R];
int less = L - 1;
int more = R;
while (L < more){
// 当前值比最右边的值小于或等于 当前值和小于区域的下一个值做交换
if (arr[L] <= pivot){
swap(arr,++less,L++);
} else {
swap(arr,L,--more);
}
}
swap(arr,less + 1,R);
// 返回小于区域的右边界
return less;
}
快排第二个版本
就是荷兰国旗问题
一开始选数组整个范围上的最后一个值作为划分值,划分出小于这个划分值的区域,等于这个划分值的区域,大于这个划分值的区域,然后将这个划分值和大于区域的第一个值做交换,则在排序过程中,此划分值在数组中的位置就不会动了
不改进的排序 :
1)划分值越靠近两侧,复杂度越高;划分值越靠近中间,复杂度越低
2)可以轻而易举的举出最差的例子,所以不改进的快速排序时间复杂度为O(N^2)
快速排序第三版本
如果划分值打在了中间,则满足master公式 T(N) = 2 * T(N/2) + O(N)
在数组的范围上[L,R],随机选择一个数作为划分值,好的情况和差的情况是等概率事件,把所有情况累加,再求数学上的长期期望,最后得到时间复杂度是 O(N*logN)
快排的额外空间复杂度O(logN)
coding
/**
* i != j
*
* @param arr
* @param i
* @param j
*/
public static void swap(int[] arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
public static void quickSort(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
quickSort(arr,0,arr.length -1);
}
public static void quickSort(int[] arr, int L, int R) {
if (L < R) {
// 随机选一个数 和最右边的数做交换
swap(arr, L + (int) (Math.random() * (R - L + 1)), R);
int[] p = partition(arr,L,R);
// p[0] 等于区域的左边界
quickSort(arr,L,p[0] - 1); // 小于区域右边界
// p[1] 等于区域的右边界
quickSort(arr,p[1] + 1,R);// 大于区域左边界
}
}
/**
*
* @param arr
* @param L 分区的左边界
* @param R 分区的右边界
* @return 划分值等于区域的左边界和右边界
*/
public static int[] partition(int[] arr, int L, int R) {
// 小于区域的左边界
int less = L - 1;
// 大于区域的右边界
int more = R;
while (L < more) { // L往右边走 more 往左边走
// arr[R] 当前的划分值
// 当前数小于划分值,当前值和小于区域的下一个值做交换
if (arr[L] < arr[R]) {
swap(arr, ++less, L++);
//当前数大于划分值 和大于区域的前一个值做交换
} else if (arr[L] > arr[R]) {
swap(arr, --more, L);
} else { // 等于的时候 直接往下走
L++;
}
}
// 大于区域的第一个数和最后一个数做交换
swap(arr, more, R);
// [等于区域的左边界,等于区域的右边界]
return new int[]{less + 1, more};
}
import java.util.Arrays;
import java.util.Stack;
/**
* @author Mrchao
* @version 1.0.0
* @date 2023-07-23
*/
public class QuickSortNonRecurTest {
public static void main(String[] args) {
int[] arr = {5,2,6,7,10,21};
quickSortNonRecur(arr);
System.out.println(Arrays.toString(arr));
}
public static void quickSortNonRecur(int[] arr){
if (arr == null || arr.length < 2){
return;
}
process(arr,0,arr.length - 1);
}
public static void swap(int[] arr,int a,int b){
int temp = arr[a];
arr[a] = arr[b];
arr[b] = temp;
}
public static void process(int[] arr,int leftBorder,int rightBorder){
Stack<Integer> indexStack = new Stack<>();
indexStack.push(rightBorder);
indexStack.push(leftBorder);
while (!indexStack.isEmpty()){
int leftIndex = indexStack.pop();
int rightIndex = indexStack.pop();
int selectIndex = leftIndex + (int) Math.random() * (rightIndex - leftIndex + 1);
swap(arr,selectIndex,rightBorder);
int[] par = partition(arr, leftIndex, rightIndex);
// 大于区域进栈
if (par[1] + 1 < rightIndex){
indexStack.push(rightIndex);
indexStack.push(par[1] + 1);
}
// 小于区域进栈
if (par[0] - 1 > leftIndex){
indexStack.push(par[0] - 1);
indexStack.push(leftIndex);
}
}
}
public static int[] partition(int[] arr,int leftIndex,int rightIndex){
int less = leftIndex - 1;
int more = rightIndex;
while (leftIndex < more){
if (arr[leftIndex] < arr[rightIndex]){
swap(arr,++less,leftIndex++);
}else if (arr[leftIndex] > arr[rightIndex]){
swap(arr,--more,leftIndex);
}else {
++ leftIndex;
}
}
swap(arr,rightIndex,more);
return new int[] {less + 1,more};
}
}
12 堆排序
1 堆结构就是用数组实现的完全二叉树结构
2 完全二叉树中如果每棵子树的最大值都在顶部就是大根堆
3 完全二叉树中如果每棵子树的最小值都在顶部就是小根堆
4 堆结构的 heapInsert与 heapify操作
5 堆结构的增大和减少
6 优先级队列结构,就是堆结构
什么是完全二叉树
若设二叉树的深度为h,除第 h 层外,其它各层 (1~h-1) 的结点数都达到最大个数,第 h 层所有的结点都连续集中在最左边,这就是完全二叉树
完全二叉树是由满二叉树而引出来的。对于深度为K的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树
完全二叉树的特点
- 叶子结点只可能在最大的两层上出现,对任意结点,若其右分支下的子孙最大层次为
L,则其左分支下的子孙的最大层次必为L 或L+1;- 出于简便起见,完全二叉树通常采用数组而不是链表存储。
- 满二叉树一定是完全二叉树,完全二叉树不一定是满二叉树。
- 完全二叉树第i层至多有
2*(i-1)个节点,共i层的完全二叉树最多有2*i-1个节点。- 只允许最后一层有空缺结点且空缺在右边,即叶子结点只能在层次最大的两层上出现;
- 对任一结点,如果其右子树的深度为j,则其左子树的深度必为
j或j+1。 即度为1的点只有1个或0个
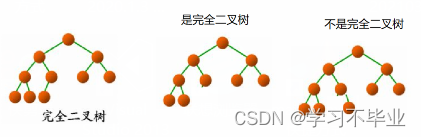
判断完全二叉树
完全二叉树:叶节点只能出现在最下层和次下层,并且最下面一层的结点都集中在该层最左边的若干位置的二叉树
将数据转换成一个完全二叉树

将数组的索引作为二叉树的节点值
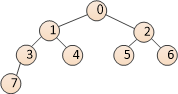
根节点索引和子树节点索引满足以下关系
设节点的索引为 i
其左子树节点的索引: 2 * i + 1
其右子树节点的索引 : 2 * i + 2
其父节点的索引为 : (i - 1 ) / 2
关于堆的两个操作
1 给定数组中某个位置的数,将这个数插入到已构建好的大根堆中 使大根堆依然是大跟堆
/**
* 将数组中给定位置的数按大根堆的方式插入到堆中
* @param arr
* @param index
*/
public static void heapInsert(int[] arr,int index){
// 当前数比父节点的数大 就一直与父节点进行替换
while (arr[index] > arr[(index - 1) /2 ]){
swap(arr,index,(index - 1) / 2);
index = index / 2;
}
}
上面的操作可以理解从堆底一直往上蹿 直到遇到不小于它的数 时间复杂度是
O(logN)
2 将堆顶的数完成调整,将堆调整成大根堆
/**
* 从指定的位置构建大根堆
* @param arr
* @param index 指定的位置
* @param heapSize 堆中数的个数 空间数据是否属于堆
*/
public static void heapify(int[] arr,int index,int heapSize){
// 左孩子的索引
int left = (2 * index) + 1;
// 存在左子节点
while (left < heapSize){
// 两个子节点中 谁的值大就把索引给谁
int largest = (left + 1 < heapSize && arr[left + 1] > arr[left])
? left + 1 : left;
// 父节点和子节点谁的值大 把值给 largest
largest = arr[largest] > arr[index] ? largest : index;
// 父节点的值比子节点的值大 不用交换 直接退出
if (largest == index){
break;
}
//较大的子节点和父节点进行交换
swap(arr,largest,index);
index = largest;
left = 2 * index + 1;
}
}
上述操作的时间复杂度也是
O(logN)
堆排序
1 先让整个数组都变成大根堆结构,建立堆的过程:
1)从上到下的方法,时间复杂度为O(N*logN)
2)从下到上的方法,时间复杂度为O(N)
2 把堆的最大值和堆末尾的值交换,然后减少堆的大小之后,再去调整堆,
一直周而复始,时间复杂度为O(N*logN)
3 堆的大小减小成0之后,排序完成
堆排序的完整代码
import java.util.Arrays;
/**
* @author Mrchao
* @version 1.0.0
* @date 2023-07-23
*/
public class HeapSortTest {
public static void main(String[] args) {
int[] arr = {10,3,7,4,6,2,8,90};
heapSort(arr);
System.out.println(Arrays.toString(arr));
}
public static void swap(int[] arr,int a,int b){
int temp = arr[a];
arr[a] = arr[b];
arr[b] = temp;
}
/**
* 将数组中给定位置的数按大根堆的方式插入到堆中
* @param arr
* @param index
*/
public static void heapInsert(int[] arr,int index){
// 当前数比父节点的数大 就一直与父节点进行替换
while (arr[index] > arr[(index - 1) /2 ]){
swap(arr,index,(index - 1) / 2);
index = index / 2;
}
}
/**
* 从指定的位置构建大根堆
* @param arr
* @param index 指定的位置
* @param heapSize 堆中数的个数 空间数据是否属于堆
*/
public static void heapify(int[] arr,int index,int heapSize){
// 左孩子的索引
int left = (2 * index) + 1;
// 存在左子节点
while (left < heapSize){
// 两个子节点中 谁的值大就把索引给谁
int largest = (left + 1 < heapSize && arr[left + 1] > arr[left])
? left + 1 : left;
// 父节点和子节点谁的值大 把值给 largest
largest = arr[largest] > arr[index] ? largest : index;
// 父节点的值比子节点的值大 不用交换 直接退出
if (largest == index){
break;
}
//较大的子节点和父节点进行交换
swap(arr,largest,index);
index = largest;
left = 2 * index + 1;
}
}
public static void heapSort(int[] arr){
if (arr == null || arr.length < 2){
return;
}
// 将数组中的所有元素加入大根堆中
/*for (int i = 0;i < arr.length;++i){
heapInsert(arr,i); // O(logN)
}*/
for(int i = arr.length - 1;i >= 0; i--){
heapify(arr,i,arr.length);
}
int heapSize = arr.length;
swap(arr,0,--heapSize);
while (heapSize > 0){// O(N)
heapify(arr,0,heapSize);// O(logN)
swap(arr,0,--heapSize);//O(1)
}
}
}
堆排序的时间复杂度
O(N * logN)额外空间复杂度O(1)
堆排序的相关算法
已知一个几乎有序的数组,几乎有序是指,如果把数组排好顺序的话,每个元素移动的距离可以不
超过k,并且k相对于数组来说比较小。请选择一个合适的排序算法针对这个数据进行排序。
/**
* 已知一个几乎有序的数组 几乎有序是指,如果把数组排好顺序的话,每个元素移动的距离可以
* 不超过k并且k相对数组来说比较小 请选择一个核实排序算法对这个数据进行排序
* @param arr
* @param k
*/
public static void sortedArrDistanceLessK(int[] arr,int k){
// 默认小根堆
PriorityQueue<Integer> heap = new PriorityQueue<>();
// 构建小根堆
int index = 0;
// 先把前k个数放在堆中
for (;index <= Math.min(arr.length,k);index++){
heap.add(arr[index]);
}
int i = 0;
// 从堆中放入一个 再取出一个
for(;index < arr.length;i++,index++){
heap.add(arr[index]);
arr[i] = heap.poll();
}
while (!heap.isEmpty()){
arr[i++] = heap.poll();
}
}