494. 目标和

力扣传送门：
https://leetcode.cn/problems/target-sum/

题目描述：

给你一个整数数组 nums 和一个整数 target 。
向数组中的每个整数前添加 ‘+’ 或 ‘-’ ，然后串联起所有整数，可以构造一个表达式：
输入：nums = [1,1,1,1,1], target = 3
输出：5
解释：一共有 5 种方法让最终目标和为 3 。
-1 + 1 + 1 + 1 + 1 = 3
+1 - 1 + 1 + 1 + 1 = 3
+1 + 1 - 1 + 1 + 1 = 3
+1 + 1 + 1 - 1 + 1 = 3
+1 + 1 + 1 + 1 - 1 = 3

动态规划解法：

解析：题目让我们在某一个或者几个位置加上符号，如果是一个负号，则就整个数组中只有正数和负数两种形式，我们不妨把这个数组看作是两个部分的和，其中一部分是正数，另一部分是负数。

left：表示正数序列的组合
right：表示负数序列的组合

如：+1 + 1 + 1 + 1 - 1 = 3 ：
则可以表示为left：是[0,3]的序列，这个序列都是正数；right：是(3,4]的组合（不包括三），他代表的是负数的子序列。

我们可以根据题意得到这两个等式：

等式一： left - right = sum（数组的原始和）
等式二： left + right = target（目标）

正数减去负数，得到的是数组原始的元素的和；正数加上负数表示的我们题目中给到的目标target。

所以，可以进一步推出此公式：
由等式一得：right = left -sum，将right带入到等式二中，得：
left + left -sum = target：

这就是我们所得到的一个关键公式：left = （target + sum）/2

得到了这个公式有什么用呢？

left = (target+sum)/2

由于 target 和 sum都是固定的，所以只有我们的left是可变的，而left又代表着什么呢？？

我们在刚才说过，left代表的是一个正数序列的组合，什么意思？

意思就是在nums[i]中选取元素，使得元素之和等于left，求所选取的元素的方案数。

我们可以把这道题看作是一个01背包的问题。

size = left

因此我们的size 就是背包的容量，本题也就是要求：
装满容量为size的背包，一共有几种方案？

我们把数组的元素nums[i]看作物品，把不同情况的元素之和size看作是背包的容量。

确定dp数组以及其下标的含义

创建dp[i][j]二维数组，其中 i 表示从数组中选取的nums[i]元素，即把某个元素看作物品；j表示背包的当前容量 j，也就是各个情况目标元素之和。
dp[i][j] 表示在数组 nums的前 i 个数中选取元素，使得这些元素之和等于 j 的方案数

确定递推公式

不选取某一个元素nums[i]： dp[i][j] = dp[i-1][j]
选取某一个元素nums[i]： dp[i][j] = dp[i-1][j] + dp[i-1][j-nums[i]]

最终我们的dp[n][size]就是答案。

dp数组的初始化：

dp[0][0] = 1

dp数组的遍历：

首先遍历物品i，其次遍历背包j

图例推导dp过程

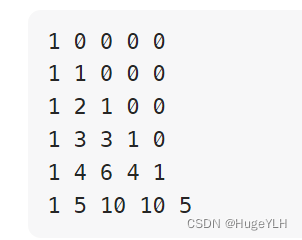
在这里插入图片描述
由此可见，我们的dp[i][j]其实就是其上方的元素与左上方的元素之和。

代码如下：

class Solution {
public:
    int findTargetSumWays(vector<int>& nums, int target) {
        int sum=accumulate(nums.begin(),nums.end(),0);
        //特殊情况1
        if (sum<abs(target))
        {
            return 0;
        }
        //特殊情况2
        if ((target+sum)%2==1)
        {
            return 0;
        }
        int size=(target+sum)/2; 
        int n=nums.size();
        vector<vector<int>> dp(n+1,vector<int>(size+1));
        dp[0][0]=1;
        for (int i=1;i<=n;i++)
        {
            int num=nums[i-1];
            for (int j=0;j<=size;j++)
            {
               if (j<num) dp[i][j]=dp[i-1][j];
               else dp[i][j]=dp[i-1][j]+dp[i-1][j-num];
            }
            
        }
        for (auto& x:dp)
            {
                for (auto& y:x)
                {
                    cout<<y<<" ";
                }
                cout<<endl;
            }
        return dp[n].back();
    }
};

dp的优化：滚动数组思想

class Solution {
public:
    int findTargetSumWays(vector<int>& nums, int target) {
        int sum=accumulate(nums.begin(),nums.end(),0);
        //特殊情况1
        if (sum<abs(target))
        {
            return 0;
        }
        //特殊情况2
        if ((target+sum)%2==1)
        {
            return 0;
        }
        int size=(target+sum)/2;   
        vector<int> dp(size+1);
        dp[0]=1;
        int n=nums.size();
        for (int i=1;i<=n;i++)
        {
            int num=nums[i-1];
            for (int j=size;j>=num;j--)
            {
                dp[j]+=dp[j-num];
            }
        }
        return dp.back();
    }
};

474. 一和零

力扣传送门：
https://leetcode.cn/problems/ones-and-zeroes/description/

本题一个三维动态规划 + 01背包的题目。
什么是三维动态规划？

二维动态规划01背包 dp[i][j]：有两个维度，即物品 i 和背包容量 j
三维动态规划01背包 dp[k][i][j]：有三个维度，本题中：k表示字符串数组中前k个字符串，i 表示0的个数，j 表示1的个数。

确定dp数组以及其下标的含义

dp[k][i][j] ：表示在前 k 个字符串中，使用最多 i 个0，j 个1，可以得到的目标字符串的个数。

递推公式的确定

不选这个字符串：dp[k][i][j] = dp[k-1][i][j]
- 此时的情况： i < zeronum && j < onenum ，即规定的 0，1的数量不足以容纳字符串中的0，1的个数，所以不能选取这个字符串
选择这个字符串：dp[k][i][j] =max(dp[k][i][j], dp[k-1][i-zeronum][j-onenum] + 1)
- 同理， i >= zeronum && j >= onenum ，规定最大的i，j，可以容纳字符串中的0，1的个数，所以可以选择这个字符串。

dp数组的初始化

dp[0][0][0] = 0，没有字符串，只能初始化为0

dp数组的遍历过程

三维：首先遍历字符串，接着在字符串中处理二维dp的物品与容量的关系。

代码如下：

class Solution {
public:
    int findMaxForm(vector<string>& strs, int m, int n) {
        int sn=strs.size();
        vector<vector<vector<int>>> dp(sn+1,
            vector<vector<int>>(m+1,vector<int>(n+1)));
        for (int k=1;k<=sn;k++)
        {
            //每次统计当前字符串中01的数量
            int zeronum=0,onenum=0;
            for (auto& num:strs[k-1])
            {
                if (num=='0') zeronum++;
                else if (num=='1') onenum++;
            }
            //二维的dp操作
            for (int i=0;i<=m;i++)
            {
                for (int j=0;j<=n;j++)
                {
                    dp[k][i][j]=dp[k-1][i][j];
                    if (i>=zeronum && j>=onenum)
                    {
                        dp[k][i][j]=max(dp[k][i][j],
                            dp[k-1][i-zeronum][j-onenum]+1);
                   }
                }
            }
        // }
        // for (auto& x:dp)
        // {
        //     for (auto& y:x)
        //     {
        //         for (auto& z:y)
        //         {
        //             cout<<z<<" ";
        //         }
        //         cout<<endl;
        //     }
        //     cout<<endl;
        // }
        return dp[sn][m][n];
    }
};

空间优化：二维数组版本

class Solution {
public:
    int findMaxForm(vector<string>& strs, int m, int n) {
        vector<vector<int>> dp(m + 1, vector<int> (n + 1, 0)); // 默认初始化0
        for (string str : strs) { // 遍历物品
            int oneNum = 0, zeroNum = 0;
            for (char c : str) {
                if (c == '0') zeroNum++;
                else oneNum++;
            }
            for (int i = m; i >= zeroNum; i--) { // 遍历背包容量且从后向前遍历！
                for (int j = n; j >= oneNum; j--) {
                    dp[i][j] = max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1);
                }
            }
        }
        return dp[m][n];
    }
};