B树
基本概述
B树又称多路平衡搜索树。一棵m阶B树,要么是空树,要么满足以下特性:
- 每个节点最多有m棵子树
- 根节点至少有两棵子树
- 内部节点(除根和叶子节点以外的节点)至少有⌈m/2⌉棵子树
- 关键字个数比子树个数少1
- 终端节点(叶子节点)在同一层上,且不带任何信息(是空节点),通常称为失败节点
基本概念
B树的阶数为m,树高为h,关键字个数为k,节点个数为n。

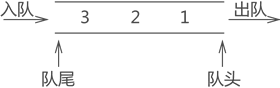
阶是B树中,所有节点的子节点个数最大的那个数。如上图所示的树,其阶数为4。
树高是指树有几层,如上图,这个树就有2层,树高也就为2。
关键字个数,如上图,关键字个数为11
节点个数,如上图,节点个数为5
每个关键字头部指向所有比它小的关键字,尾部指向所有比它大的关键字
B树的排序
B树是有排序的,对应一个排序数组。
在具有k个关键字的B树中,查找失败有k+1种情况,且均为叶子节点。
最小树高和最小节点数
要让树高最小,那么每层的节点个数就要最大,即每个节点的子节点个数要最大,而m阶B树,其子节点的个数最大为m,那么我们让每个节点的子节点个数都为m,这样就能推导出最小树高。
| 第X层 | 节点个数 |
|---|---|
| 0 | 1 |
| 1 | m |
| 2 | m^2 |
| 3 | m^3 |
| … | … |
| h - 1 | m^(h-1) |
| h | m^h |
失败节点个数为mh,则mh = k + 1
即:
h >= log(k + 1)
最小节点数:
n = k / (m - 1)
最大树高与最大节点数
与上面最小类似,最大只有让每个节点的子节点个数最小就好。
| 第X层 | 节点个数 |
|---|---|
| 0 | 1 |
| 1 | 2 |
| 2 | 2⌈m / 2⌉ |
| 3 | 2⌈m / 2⌉^2 |
| … | … |
| h - 1 | 2⌈m / 2⌉^(h-2) |
| h | 2⌈m / 2⌉^(h-1) |
2⌈m / 2⌉^(h-1) = k + 1
所以:
h≤log_⌈m/2⌉ ((k+1)/2)+1
根节点最少可以只有1个关键字,而其他节点最少需要⌈m/2⌉-1个关键字。考虑根节点补齐到⌈m/2⌉-1个关键字,则总关键字个数k需要增加⌈m/2⌉-2个。因此最大节点数为:
n≤(k+⌈m/2⌉-2)/(⌈m/2⌉-1)
B+树
B树中,每个节点都存有key-value,为了节省存储空间,可以采用B+树,在每个节点中,仅存储key即可。
B树有两种结构:

其中第2中结构比第一种结构更节省空间,且与B树更相似,因此也主要以第2种结构为主。第2种结构B+树的特征与B树相似,差别为:最后一层非叶子节点包含了全部的关键字,且节点间按升序顺序连接。