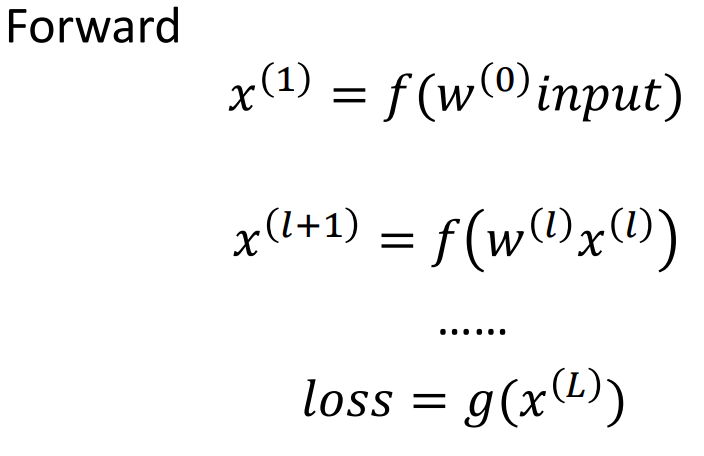题目：

示例：

分析：

题目描述的有点复杂,~~特别是那个公式,一看到我就烦~~.

其实意思就是找出一个子数组(连续),要求这个子数组的和是所有子数组中最大的,并且这个数组是环形的,意思就是我这个子数组可以从原数组的尾部开始,到原数组的头部结束,就是原数组的首尾是连同的.

那么我第一反应就是将原数组后面再连接一个原数组得到新数组,例如这样:

这样就是首尾相连了,并且只要我把子数组的长度控制在小于等于原数组,那么取到的子数组就是等于在原数组首尾相连的情况下取到的子数组(即不会重复取同一个元素).

这时候再取前缀和,获取最大的子数组和(长度要控制在小于等于原数组),将两个索引的前缀和相减就是两个索引之间的元素之和(不理解的同学再仔细理解理解):

代码在下面,总之结果是超时,就是提供一种思路.(~~回头看看代码,发现时间复杂度确实有点高~~)

以下思路参考力扣外国站大佬,大佬的思路确实厉害:

LeetCode - The World's Leading Online Programming Learning Platform

我们可以发现要取首尾相连的数组的最大子数组和,其实一共就两种情况,一种是常规情况,子数组就在原数组的中间:

另外一种情况是这样的,子数组的开头在原数组的末尾,结尾在子数组的开头:

如果是第一种情况,我们就可以参考力扣第53题最大子数组和,那题和本题基本一致,只不过本题的数组是头尾相连的,但如果是第一种情况,就没有利用到首尾相连的这一特性,因此可以直接套用53题的解法(具体思路就不说了,直接看代码叭)

//https://leetcode.cn/problems/maximum-subarray/
class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        vector<int>dp(nums.size(),nums[0]);
        int res=dp[0];
        for(int i=1;i<nums.size();i++){
            dp[i]=max(0,dp[i-1])+nums[i];
            res=max(res,dp[i]);
        }
        return res;
    }
};

那么我们就算是把第一种情况给解决掉了,此时就剩第二种情况,其实第二种情况我们可以发现和第一种情况也很想,都是在原数组的中间有这么一段连续子数组,那么它们这两段连续的子数组有什么联系呢?

我们可以发现在第一种情况中,在原数组中间的的这段连续子数组是所有子数组里和最大的子数组,也就是我们要求的.

而第二种情况中,在原数组中间的这段连续子数组是什么,我们乍一看还看不出来是什么,其实中间这段是所有子数组里和最小的子数组,我把一个首尾相连的数组里和最小的连续子数组删去,剩下的不就是我能凑到的和最大的连续子数组了?

可能不太好理解,我举一个比较极端的例子给大家看看:

如上图所示,中间这段是连续子数组的和为-200,而整个数组的和为-196,如果我把中间的~~害群之马~~和最小的子数组删掉,那么得到的首尾相连的最大子数组的和不就是整个数组的和减去最小连续子数组的和等于 -196-(-200) =4 了?

那么我们就算是找到规律了,我们只需要按照上面53题的做法使用动态规划来分别获取在首尾不相连的情况下,最大的连续子数组和最小的连续子数组,再分别比较第一种情况和第二种情况即可.

假设为第一种情况,那么结果就是找出的最大连续子数组的和.假设是第二种情况,那么结果就是整个数组的和减去最小的连续子数组.在两种情况都假设完之后,返回结果最大的一种情况.

但其实我们忽略了另一种极端情况,那就是整个数组都是负数的情况.

在这种情况下,我们应该返回的是整个数组中最小的那个负数,但按照我们上面的推导,我们会返回0,因为我们求出来最大的连续子数组的和确实是整个数组中最小的负数,但是整个数组的和减去最小的连续子数组的和的结果却是0(最小的连续子数组就是整个数组,如果整个数组减去最小的连续子数组就相当于是我们一个元素都不取,但是这样是不符合题意的,我们至少需要取一个),比最大的连续子数组的和更大,因此在整个数组都是负数的情况下我们返回的是0.

我们只需要在返回结果的时候多一个判断就可以了:

return Max>0 ? max(Max,Sum-Min) : Max;

在最大的连续子数组的和大于0的时候我们再比较两种情况谁更大,然后返回更大的一个数.

如果最大的连续子数组的和小于0,这时就是整个数组都是负数的情况了,我们则不用比较,直接返回最大的连续子数组的和就可以了.

代码+运行结果：

前缀和,但是超时,提供一种解题思路.

class Solution {
public:
    int maxSubarraySumCircular(vector<int>& nums) {
        //前缀和超时
        int n=nums.size();
        int res=nums[0];
        int temp=0;
        vector<int>newNums(2*n),tempNums(2*n);
        for(int i=0;i<2;i++){
            for(int j=0;j<n;j++) newNums[i*n+j]=nums[j];
        }
        for(int i=0;i<2*n;i++){
            tempNums[i]=temp;
            temp+=newNums[i];
        }
        for(int i=0;i<n;i++){
            for(int j=i+1;j<2*n && j-i<n+1;j++){
                res=max(res,tempNums[j]-tempNums[i]);
            }
        }
        return res;
    }
}

class Solution {
public:
    int maxSubarraySumCircular(vector<int>& nums) {
        //参考的https://leetcode.com/problems/maximum-sum-circular-subarray/solutions/178422/One-Pass/的动态规划
        int n=nums.size();
        vector<vector<int>>dp(2,vector<int>(n,nums[0]));
        int Max=nums[0],Min=nums[0],Sum=nums[0];
        for(int i=1;i<n;i++){
            Sum+=nums[i];
            dp[0][i]=max(0,dp[0][i-1])+nums[i];
            dp[1][i]=min(0,dp[1][i-1])+nums[i];
            Max=max(Max,dp[0][i]);
            Min=min(Min,dp[1][i]);
        }
        return Max>0 ? max(Max,Sum-Min) : Max;
    }
};