外参矩阵转四元数,左右手坐标系转化1_天人合一peng的博客-CSDN博客
在之前1的基础上更新
通过定位已经求得了物体的4*4的位姿矩阵,将其变化为四元数并从opengl的右手坐标转化为unity的左手坐标系。
body2world_pose().matrix()为计算得到的4*4的位姿矩阵
例
body1_world2body_pose.matrix() <<
1.0f, 0.0f, 0.0f, 0.095f,
0.0f, 1.0f, 0.0f, 0.1f,
0.0f, 0.0f, 1.0f, -0.4f,
0.0f, 0.0f, 0.0f, 1.0f;
------------------------------C++ dll----------------------------
Eigen::Matrix<float, 4, 4> matrix_body2world_pose;
//Eigen::Matrix<float, 3, 3> matrix_rotation;
Eigen::Matrix3d matrix_rotation;
Eigen::Quaterniond matrix_quarternion;
matrix_body2world_pose = body1_ptr->body2world_pose().matrix();
//body1_ptr->geometry2world_pose().matrix();
//for (size_t i = 0; i < 4; i++)
//{
// for (size_t j = 0; j < 4; j++)
// {
// std::cout << matrix_body2world_pose(i, j) << "\t";
// }
//}
//取出旋转矩阵
for (size_t i = 0; i < 3; i++)
{
for (size_t j = 0; j < 3; j++)
{
matrix_rotation(i, j) = matrix_body2world_pose(i, j);
}
}
//matrix_rotation(0, 2) *= -1;
//matrix_rotation(1, 2) *= -1;
//matrix_rotation(2, 0) *= -1;
//matrix_rotation(2, 1) *= -1;
//将旋转矩阵转化为四元数
matrix_quarternion = Eigen::Quaterniond(matrix_rotation);
//std::cout << "---------------matrix_quarternion-----------------" << std::endl;
std::cout << matrix_quarternion << std::endl;
//std::cout << matrix_quarternion.x() << "\t" <<matrix_quarternion.y() << "\t"
// << matrix_quarternion.z() << "\t" << matrix_quarternion.z() << "\t" << std::endl;
//右手坐标转化为左手坐标:旋转 x,z取反,平移y取反
保存表示旋转的四元数和平移的值
float location[7] = { -matrix_quarternion.x(), matrix_quarternion.y(), -matrix_quarternion.z(), matrix_quarternion.w(),
matrix_body2world_pose(0, 3), -matrix_body2world_pose(1, 3),matrix_body2world_pose(2, 3) };
memcpy(pos_array, location, sizeof(float) * 7);
另一种求四元数方法
//计算四元数
int sign(float x)
{
return x >= 0 ? 1 : -1;
}
float myMax(float x, float y)
{
return x > y ? x : y;
}
void QuaternionFromMatrix(const cv::Mat& R, float quat[])
{
// Adapted from: http://www.euclideanspace.com/maths/geometry/rotations/conversions/matrixToQuaternion/index.htm
/*quat[0] = (float)sqrt(myMax(0.0, 1 + R.ptr<float>(0)[0] + R.ptr<float>(1)[1] + R.ptr<float>(2)[2]))/2;
quat[1] = (float)sqrt(myMax(0.0, 1 + R.ptr<float>(0)[0] - R.ptr<float>(1)[1] - R.ptr<float>(2)[2]))/2;
quat[2] = (float)sqrt(myMax(0.0, 1 - R.ptr<float>(0)[0] + R.ptr<float>(1)[1] - R.ptr<float>(2)[2]))/2;
quat[3] = (float)sqrt(myMax(0.0, 1 - R.ptr<float>(0)[0] - R.ptr<float>(1)[1] + R.ptr<float>(2)[2]))/2;
quat[1] *= sign(R.ptr<float>(2)[1] - R.ptr<float>(1)[2]);
quat[2] *= sign(R.ptr<float>(0)[2] - R.ptr<float>(2)[0]);
quat[3] *= sign(R.ptr<float>(1)[0] - R.ptr<float>(0)[1]);*/
//R.convertTo(R, CV_32F);
quat[0] = (float)sqrt(myMax(0.0, 1 + R.at<float>(0, 0) + R.at<float>(1, 1) + R.at<float>(2, 2))) / 2;
quat[1] = (float)sqrt(myMax(0.0, 1 + R.at<float>(0, 0) - R.at<float>(1, 1) - R.at<float>(2, 2))) / 2;
quat[2] = (float)sqrt(myMax(0.0, 1 - R.at<float>(0, 0) + R.at<float>(1, 1) - R.at<float>(2, 2))) / 2;
quat[3] = (float)sqrt(myMax(0.0, 1 - R.at<float>(0, 0) - R.at<float>(1, 1) + R.at<float>(2, 2))) / 2;
quat[1] *= sign(R.at<float>(2, 1) - R.at<float>(1, 2));
quat[2] *= sign(R.at<float>(0, 2) - R.at<float>(2, 0));
quat[3] *= sign(R.at<float>(1, 0) - R.at<float>(0, 1));
//quat[0]为w, quat[1]为x, quat[2]为y, quat[3]为z
}
另一种方法计算四元数
cv::Mat body_r = cv::Mat(3, 3, CV_32F);
cv::Mat matrix_r = cv::Mat(3, 3, CV_32F);
//取出旋转矩阵
for (size_t i = 0; i < 3; i++)
{
for (size_t j = 0; j < 3; j++)
{
matrix_r.at<float>(i,j) = matrix_body2world_pose(i, j);
}
}
float siyuanshu[4] = { 0, 0, 0, 0 };
QuaternionFromMatrix(matrix_r, siyuanshu);
cv::Mat matrix_trans = cv::Mat(3, 1, CV_32F);
matrix_trans.at<float>(0, 0) = matrix_body2world_pose(0, 3);
matrix_trans.at<float>(1, 0) = matrix_body2world_pose(1, 3);
matrix_trans.at<float>(2, 0) = matrix_body2world_pose(2, 3);
//右手坐标转化为左手坐标:旋转 x,z取反,平移y取反
保存表示旋转的四元数和平移的值
float location[7] = { siyuanshu[0], -siyuanshu[1], siyuanshu[2], -siyuanshu[3],
matrix_body2world_pose(0, 3), -matrix_body2world_pose(1, 3), matrix_body2world_pose(2, 3) };
memcpy(pos_array, location, sizeof(float) * 7);------------------------------------------------------unity---------------------------------
using System.Collections;
using System.Collections.Generic;
using UnityEngine;
using System.Runtime.InteropServices;
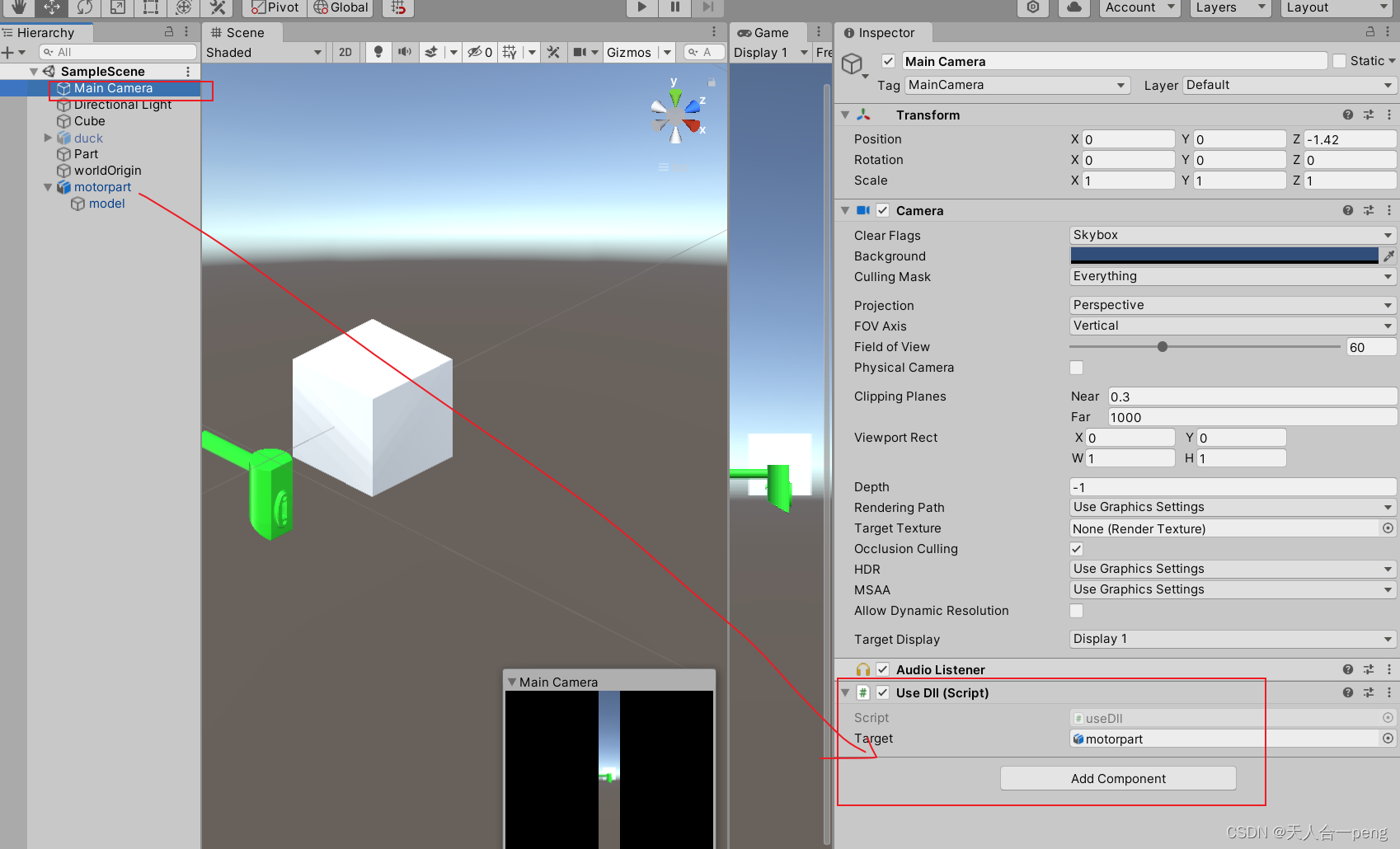
public class useDll : MonoBehaviour
{
[DllImport("run_on_camera_sequence")]
static extern void main();
[DllImport("run_on_camera_sequence")]
static extern int start_track(int iteration, float[] pos_array, int[] is_update);
private float[] pos_array = new float[7];
private int[] is_update = new int[2];
bool stop_run = false;
public GameObject Target;
int iteration = 0;
// Start is called before the first frame update
void Start()
{
main();
//print(is_update[0]);
}
// Update is called once per frame
void Update()
{
start_track(iteration, pos_array, is_update);
iteration += 1;
// unity Quaternion的赋值顺序是x,y,z,w
//Target.transform.localRotation = new Quaternion( pos_array[1], pos_array[2], pos_array[3], pos_array[0]);
Target.transform.localRotation = new Quaternion(pos_array[0], pos_array[1], pos_array[2], pos_array[3]);
Target.transform.localPosition = new Vector3(pos_array[4], pos_array[5], pos_array[6]);
print("-------[0]------" + is_update[0] + "-------[1]------" + is_update[1]);
}
}
在unity赋值是一定是先赋旋转再赋平移才会正确,先后不一样,因为,旋转先赋值相当于在坐标原点旋转这和其不在坐标原点的旋转效果一样,但如果先平移,后再旋转就不是一回事了。
unity里面先将物体的旋转调整为opengl沉浸的和unity中相机看的一样。我想这个是必须的?为什么呢,物体的位姿是实时给------------------但实事证明这样是对的。
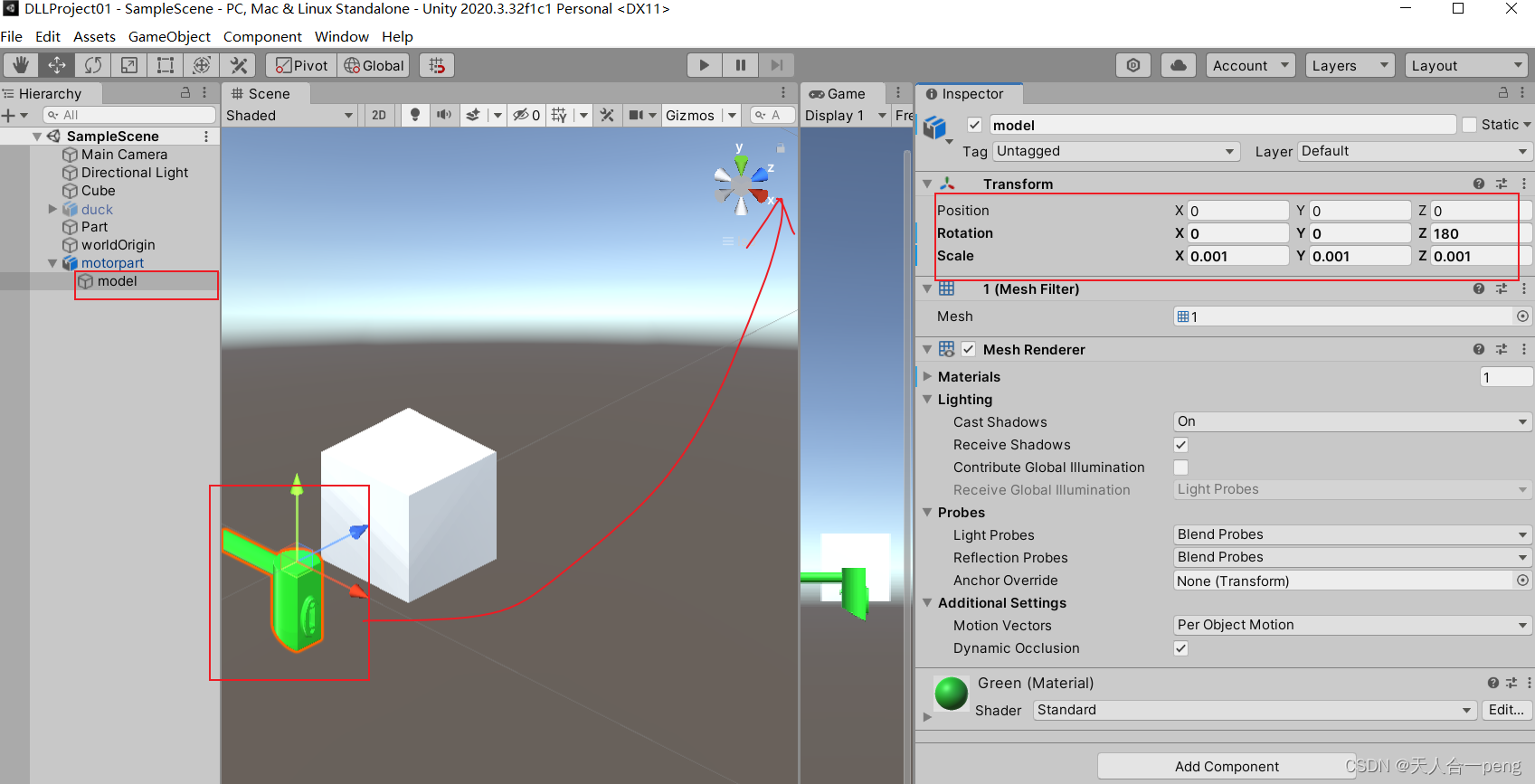
然后在motopart上给物体赋值