---

PyTorch——开源的Python机器学习库

一、前言

  本想着一篇博文直接写完基于PyTorch的深度学习实战，可写着写着发现字数都上万了。考虑到读者可能花了大力气对这么一篇博文看到失去了对PyTorch神经网络的耐心，同时也为了我个人对文章排版的整理，还是分成了分卷阅读。
  这里贴一下上篇博文：
[深度学习实战]基于PyTorch的深度学习实战(上)[变量、求导、损失函数、优化器]
  还有贴上博文的社区帖子：
[有红包][深度学习实战]基于PyTorch的深度学习实战(上)[变量、求导、损失函数、优化器]

---

二、线性回归

  线性回归也叫 regression，它是一个比较简单的模拟线性方程式的模型。线性方程式我们应该都学过吧，就是类似这样：
  Y=wX+b
  其中 w 是系数，b 是位移，它是一条笔直的斜线。

  那么我们假设给定一条模拟直线的点，每个点偏移这条直线很小的范围，我们要用到随机函数来模拟这个随机的偏移。
  首先可以定义一个随机种子，随机种子基本不影响随机数的值，也可以不定义随机种子。随机数值在 0～1 之间。
  例如：torch.manual_seed(1)，设置随机种子为 1。

size=10
0.2*torch.rand(size)

  这里我们不打算使用 pytorch 的随机函数，毕竟 numpy 中已经提供了随机函数，我们的数据是生成 200 个 X 和 Y，模拟参数 w 为 0.5。
  代码：

import numpy as np
from numpy import random
import matplotlib.pyplot as plt
X = np.linspace(-1, 1, 200)
Y = 0.5 * X + 0.2* np.random.normal(0, 0.05, (200, ))
plt.scatter(X,Y)
plt.show()
#将X，Y转成200 batch大小，1维度的数据
X=Variable(torch.Tensor(X.reshape(200,1)))
Y=Variable(torch.Tensor(Y.reshape(200,1)))

  图形：

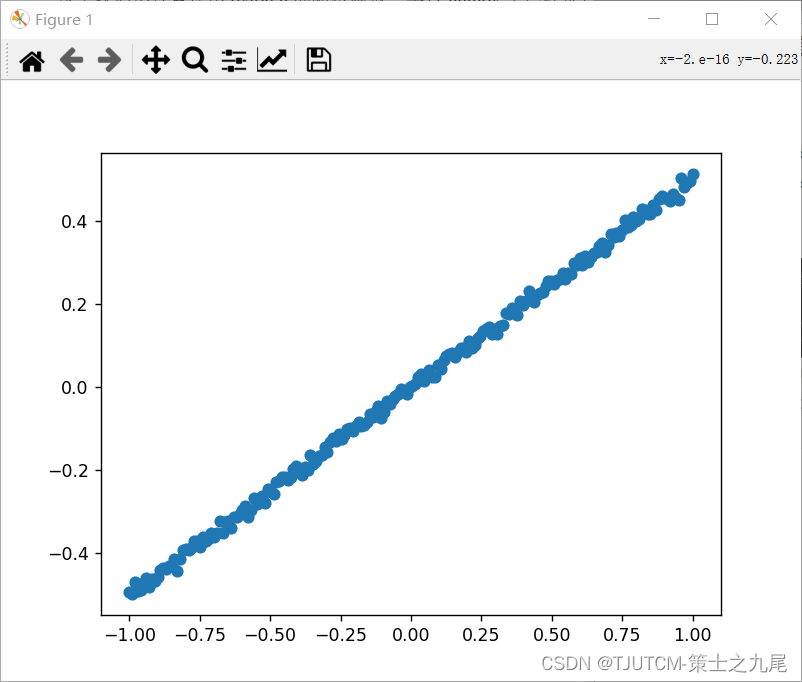
  注意：这里要将输入数据转换成 (batch_size,dim) 格式的数据，添加一个批次的维度。
  现在的任务是给定这些散列点 (x,y) 对，模拟出这条直线来。这是一个简单的线性模型，我们先用一个简单的 1→1 的 Linear 层试试看。
  示例代码：

# 神经网络结构
model = torch.nn.Sequential(
torch.nn.Linear(1, 1),
)
optimizer = torch.optim.SGD(model.parameters(), lr=0.5)
loss_function = torch.nn.MSELoss()

2.1 训练代码

for i in range(300):
prediction = model(X)
loss = loss_function(prediction, Y)
optimizer.zero_grad()
loss.backward()
optimizer.step()

2.2 绘图部分代码

plt.figure(1, figsize=(10, 3))
plt.subplot(131)
plt.title('model')
plt.scatter(X.data.numpy(), Y.data.numpy())
plt.plot(X.data.numpy(), prediction.data.numpy(), 'r-', lw=5)
plt.show()

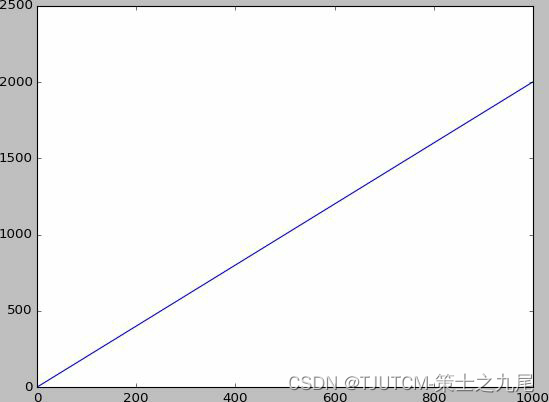
  最后的显示结果如图所示，红色是模拟出来的回归曲线：

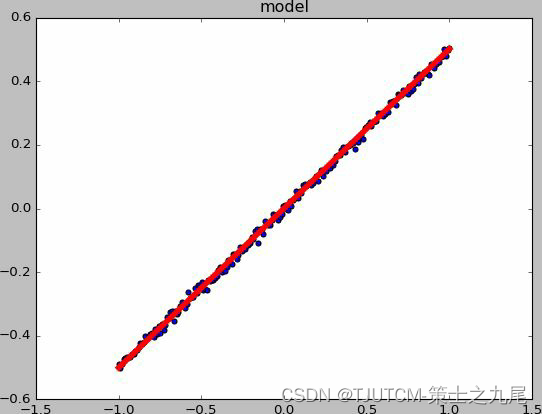
2.3 numpy 数组的保存和导入代码

np.save("pred.npy",prediction.data.numpy())
pred= numpy.load("pred.npy")

2.4 完整代码

import numpy as np
from numpy import random
import matplotlib.pyplot as plt
import torch
from torch.autograd import Variable
X = np.linspace(-1, 1, 200)
Y = 0.5 * X + 0.2* np.random.normal(0, 0.05, (200, ))
X=Variable(torch.Tensor(X.reshape(200,1)))
Y=Variable(torch.Tensor(Y.reshape(200,1)))
print(X)
model = torch.nn.Sequential(
torch.nn.Linear(1, 1)
)
optimizer = torch.optim.SGD(model.parameters(), lr=0.5)
loss_function = torch.nn.MSELoss()
for i in range(300):
prediction = model(X)
loss = loss_function(prediction, Y)
print("loss:",loss)
optimizer.zero_grad()
loss.backward()
optimizer.step()
print(prediction.data.numpy())
plt.figure(1, figsize=(10, 3))
plt.subplot(131)
plt.title('model')
plt.scatter(X.data.numpy(), Y.data.numpy())
plt.plot(X.data.numpy(), prediction.data.numpy(), 'r-', lw=5)
plt.show()

---

三、numpy矩阵的保存

import numpy as np
a=np.array(2)
np.save("nm.npy",a)
a = np.load("nm. npy ")

  其中 np 是 import numpy as np 的 np。a 是对应的 numpy 数组，"nm. npy"是文件名称。

---

四、模型的保存和导入

  每次定义和训练一个模型都要花费很长的时间，我们当然希望有一种方式可以将训练好的模型和参数保存下来，下一次使用的时候直接导入模型和参数，就跟一个已经训练好的神经网络模型一样。幸运的是，pytorch 提供了保存和导入方法。

---

4.1 保存模型

# 保存整个神经网络的结构和模型参数
torch.save(mymodel, 'mymodel.pkl')
# 只保存神经网络的模型参数
torch.save(mymodel.state_dict(), 'mymodel_params.pkl')

---

4.2 导入模型

mymodel = torch.load('mymodel.pkl')

---

五、卷积层

  卷积层是用一个固定大小的矩形区去席卷原始数据，将原始数据分成一个个和卷积核大小相同的小块，然后将这些小块和卷积核相乘输出一个卷积值（注意：这里是一个单独的值，不再是矩阵了）。
  卷积的本质就是用卷积核的参数来提取原始数据的特征，通过矩阵点乘的运算，提取出和卷积核特征一致的值，如果卷积层有多个卷积核，则神经网络会自动学习卷积核的参数值，使得每个卷积核代表一个特征。
  这里我们拿最常用的 conv2d 和 conv1d 举例说明卷积过程的计算。

---

5.1 Conv2d

  conv2d 是二维度卷积，对数据在宽度和高度两个维度上进行卷积。

5.1.1 函数定义

torch.nn.functional.conv2d(input, weight, bias=None, stride=1, padding=0, dilation

5.1.2 参数说明

  input：输入的Tensor数据，格式为 (batch,channels,H，W)，四维数组，第一维度是样本数量，第二维度是通道数或者记录数，三、四维度是高度和宽度。
  weight：卷积核权重，也就是卷积核本身，是一个四维度数组，(out_channels, in_channels/groups, kH, kW)。 Out_channels 是卷积核输出层的神经元个数，也就是这层有多少个卷积核；==in_channels ==是输入通道数，kH 和 kW 是卷积核的高度和宽度。
  bias：位移参数，可选项，一般不用管。
  stride：滑动窗口，默认为 1，指每次卷积对原数据滑动 1 个单元格。
  padding：是否对输入数据填充 0。Padding 可以将输入数据的区域改造成卷积核大小的整数倍，这样对不满足卷积核大小的部分数据就不会忽略了。通过 padding 参数指定填充区域的高度和宽度，默认 0（就是填充区域为0，不填充的意思）。
  dilation：卷积核之间的空格，默认1。
  groups：将输入数据分组，通常不用管这个参数，没有太大意义。

5.1.3 测试代码

import torch
from torch.autograd import Variable
import torch.nn as nn
import torch.nn.functional as F
print("conv2d sample")
a=torch.ones(4,4)
x = Variable(torch.Tensor(a))
x=x.view(1,1,4,4)
print("x variable:", x)
b=torch.ones(2,2)
b[0,0]=0.1
b[0,1]=0.2
b[1,0]=0.3
b[1,1]=0.4
weights = Variable(b)
weights=weights.view(1,1,2,2)
print ("weights:",weights)
y=F.conv2d(x, weights, padding=0)
print ("y:",y)

5.1.4 最终结果

  我们看看它是怎么计算的：
  （1） 原始数据大小是1 * 1 * 4 * 4，1 * 1我们忽略掉，就是一个样本，每个样本一个通道的意思。4 * 4说明每个通道的数据是4 * 4大小的。而卷积核的大小是2 * 2。最后的卷积结果是3 * 3。

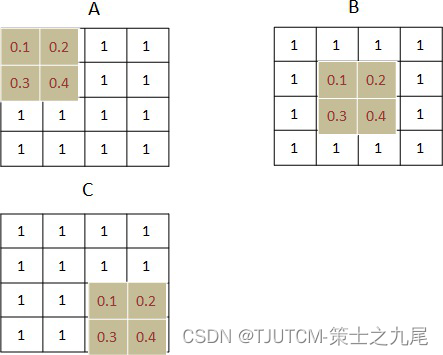
  A. 第一步，卷积核与原始数据第一个数据做卷积乘法。图中示例部分的算法如下：
  0.1 * 1+0.2 * 1+0.3 * 1+0.4 * 1=1.0。
  B. 中间步骤，按顺序移动卷积核，并和目标区域做矩阵乘法。得到这一步的卷积值，作为结果矩阵的一个元素，图中示例部分的算法如下：
  0.1 * 1+0.2 * 1+0.3 * 1+0.4 * 1=1.0
  C. 最后一步，用卷积核卷积 input[2:4,2:4]，最后共 4 个元素。图中示例部分的算法和上面一样，最后的值也是 1。
  因为原始数据都是 1，所有最后卷积出来的结果才是相同的，否则的话是不同的。最终卷积的结果就是：

---

5.2 Conv1d

   conv1d 是一维卷积，它和 conv2d 的区别在于只对宽度进行卷积，对高度不卷积。

5.2.1 函数定义

torch.nn.functional.conv1d(input, weight, bias=None, stride=1, padding=0, dilation=

5.2.2 参数说明

  input：输入的Tensor数据，格式为 (batch,channels,W)，三维数组，第一维度是样本数量，第二维度是通道数或者记录数，三维度是宽度。
  weight：卷积核权重，也就是卷积核本身。是一个三维数组，(out_channels, in_channels/groups, kW)。 out_channels 是卷积核输出层的神经元个数，也就是这层有多少个卷积核；in_channels 是输入通道数；kW 是卷积核的宽度。
  bias：位移参数，可选项，一般也不用管。
  stride：滑动窗口，默认为 1，指每次卷积对原数据滑动 1 个单元格。
  padding：是否对输入数据填充 0。Padding 可以将输入数据的区域改造成是卷积核大小的整数倍，这样对不满足卷积核大小的部分数据就不会忽略了。通过 padding 参数指定填充区域的高度和宽度，默认 0（就是填充区域为0，不填充的意思）。
  ilation：卷积核之间的空格，默认 1。
  groups：将输入数据分组，通常不用管这个参数，没有太大意义。

5.2.3 测试代码

import torch
from torch.autograd import Variable
import torch.nn as nn
import torch.nn.functional as F
print("conv1d sample")
a=range(16)
x = Variable(torch.Tensor(a))
x=x.view(1,1,16)
print("x variable:", x)
b=torch.ones(3)
b[0]=0.1
b[1]=0.2
b[2]=0.3
weights = Variable(b)
weights=weights.view(1,1,3)
print ("weights:",weights)
y=F.conv1d(x, weights, padding=0)
print ("y:",y)

5.2.4 最终结果

  我们看看它是怎么计算的：
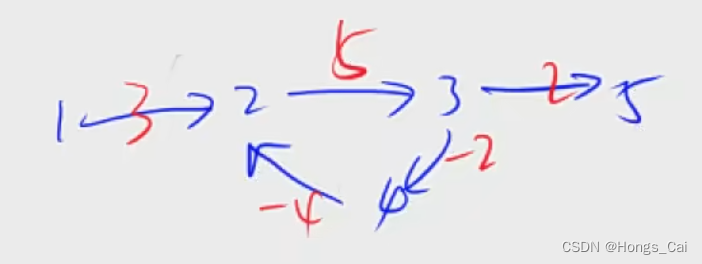
  （1）原始数据大小是 0-15 的一共 16 个数字，卷积核宽度是 3，向量是 [0.1,0.2,0.3]。
  我们看第一个卷积是对 x[0:3] 共 3 个值 [0,1,2] 进行卷积，公式如下：
0 * 0.1+1 * 0.2+2 * 0.3=0.8
  （2）对第二个目标卷积，是 x[1:4] 共 3 个值 [1,2,3] 进行卷积，公式如下：
1 * 0.1+2 * 0.2+3 * 0.3=1.4
  看到和计算结果完全一致！

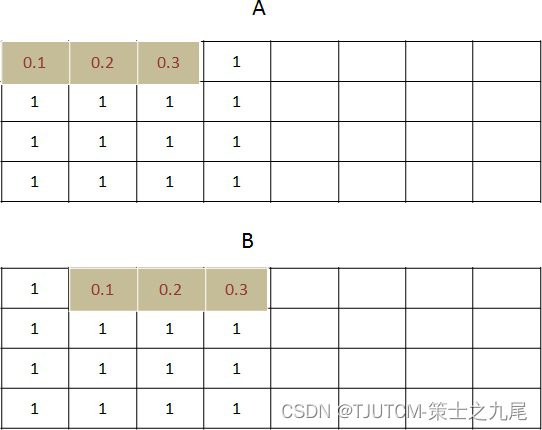
  该图就是conv1d的示意图，和conv2d的区别就是只对宽度卷积，不对高度卷积。最后结果的宽度是原始数据的宽度减去卷积核的宽度再加上
1，这里就是 14。
  所以最终卷积之后的结果一共是 14 个数值，显示如下：

  我们再看看输入数据有多个通道的情况：

5.2.5 核心代码

print("conv1d sample")
a=range(16)
x = Variable(torch.Tensor(a))
x=x.view(1,2,8)
print("x variable:", x)
b=torch.ones(6)
b[0]=0.1
b[1]=0.2
b[2]=0.3
weights = Variable(b)
weights=weights.view(1,2,3)
print ("weights:",weights)
y=F.conv1d(x, weights, padding=0)
print ("y:",y)

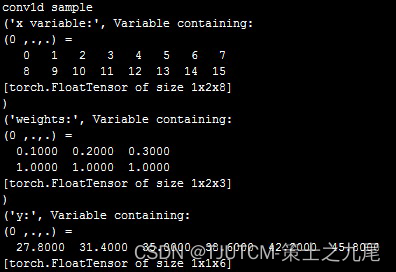
  我们看看返回结果第一个元素 27.8 是怎么计算出来的，这时候卷积核有 2 个通道：
[0.1,0.2,0.3] 和 [1,1,1]
  第 1 个卷积对象也有 2 个通道：[0,1,2] 和 [8,9,10]
  结果是 2 个卷积核分别对应 2 个输入通道进行卷积然后求和。
  卷积核对第 1 个卷积对象的卷积值：(0.1 * 0+0.2 * 1+0.3 * 2)+(1 * 8+1 * 9+1 * 10)=27.8
  第2个卷积对象也有 2 个通道：[1,2,3] 和 [9,10,11]
  卷积核对第 2 个卷积对象的卷积值：(0.1 * 1+0.2 * 2+0.3 * 3)+(1 * 9+1 * 10+1 * 11)=31.4，和 pytorch 计算结果相同。

---

六、池化层

  池化层比较容易理解，就是将多个元素用一个统计值来表示。
  那为什么要池化呢？
  比如对于一个图像来说，单个的像素其实不代表什么含义。统计值可以取最大值，也可以取平均值，用不同的池化函数来表示。

---

6.1 max_pool2d

  对于二维最大值池化来说，用 torch.nn.functional. F.max_pool2d 方法来操作。
  比如：

import torch.nn.functional as F
from torch.autograd import Variable
print("conv2d sample")
a=range(20)
x = Variable(torch.Tensor(a))
x=x.view(1,1,4,5)
print("x variable:", x)
y=F.max_pool2d(x, kernel_size=2,stride=2)
print ("y:",y)

  最后显示结果如下图：

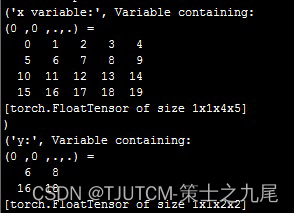
  x 是 4*5 的矩阵，表示高度 4，宽度 5，一个样本，每个样本一个通道。
  x=x.view(1,1,4,5) 意思是将 x 矩阵转换成 (1,1,4,5) 的四维矩阵，第一个 1 是样本数，第二个 1 是通道数，第三个 4 和第四个 5 是高度和宽度。
  b=F.max_pool2d(x, kernel_size=2,stride=2) 中的参数 2 表示池化的核大小是 2，也就是 (2,2)，表示核是一个行 2 列 2 的矩阵，每两行两列池化成一个数据。比如：
  [[1,2],
  [3,4]]
  会被池化成最大的数，就是 4。
  stride=2 表示滑动窗口为 2，第一个池化对象之后相隔 2 个元素距离，如果剩下的不够池化核的尺寸，则忽略掉不作池化处理。
  第 1 个池化目标是 [[0,1],[5,6]]，因此最大池化结果是 6；第 2 个池化目标是 [[2,3],[7,8]]，因此最大池化结果是 8。
  max_pool2d 方法的说明如下：

torch.nn.functional.max_pool2d(input, kernel_size, stride=None, padding=0, dilation=1

  那么具体的各个参数的含义说明如下：
  input：输入的 Tensor 数据，格式为 (channels,H，W)，三维数组，第一维度是通道数或者记录数，二、三维度是高度和宽度。
  kernel_size：池化区的大小，指定宽度和高度 (kh x kw)，如果只有一个值则表示宽度和高度相同。
  stride：滑动窗口，默认和 kernel_size 相同值，这样在池化的时候就不会重叠。如果设置的比 kernel_size 小，则池化时会重叠。它也是高度和宽度两个值。
  padding：是否对输入在左前端填充 0。池化时，如果剩余的区域不够池化区大小，则会丢弃掉。 Padding 可以将输入数据的区域改造成是池化核的整数倍，这样就不会丢弃掉原始数据了。Padding 也是指定填充区域的高度和宽度，默认 0（就是填充区域为 0，不填充的意思）。
  ceil_mode：在计算输出 shape 大小时按照 ceil 还有 floor 计算，是数序函数（如ceil(4.5)=5;floor(4.5)=4）。
  count_include_pad：为 True 时，在求平均时会包含 0 填充区域的大小。这个参数只有在 avg_pool2d 并且 padding 参数不为 0 时才有意义。

---

6.2 avg_pool2d

  那么同样的，avg_pool2d 和 max_pool2d 的计算原理是一样的！只不过avg_pool2d 取的是平均值，而不是最大值而已。这里就不重复说明计算过程了。

---

6.3 max_pool1d

  max_pool1d 和 max_pool2d 的区别和卷积操作类似，也是只对宽度进行池化。
  先看看示例代码：

print("conv1d sample")
a=range(16)
x = Variable(torch.Tensor(a))
x=x.view(1,1,16)
print("x variable:", x)
y=F.max_pool1d(x, kernel_size=2,stride=2)
print ("y:",y)

  输出结果：

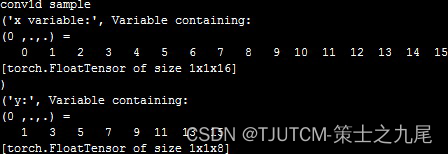
  max_pool1d 方法对输入参数的最后一个维度进行最大池化。
  第一个池化目标 [0,1]，池化输出 1；
  第二个池化目标 [2,3]，池化输出 3；
  ……
  最后结果就是这样计算得来的。
  同样，我们仿照卷积操作再看看多通道的池化示例。代码：

print("conv1d sample")
a=range(16)
x = Variable(torch.Tensor(a))
x=x.view(1,2,8)
print("x variable:", x)
y=F.max_pool1d(x, kernel_size=2,stride=2)
print ("y:",y)

  输出结果：

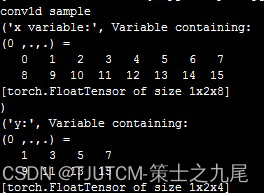
  可以看到通道数保持不变。

---

七、后记

  好的，恭喜你看完了本文的全部内容！其余的知识点，会在基于PyTorch的深度学习实战的下篇和补充篇分享，会在下周放出！如果有兴趣跟着我学习的话，请在这周复习回顾并尽量手敲代码来体验并加深理解。下周见！