L0 范数、L1 范数、L2 范数、余弦距离
向量的范数可以简单形象理解为向量的长度,或者向量到零点的距离,亦或是相应两个点之间的距离。因此范数通常会对应一个距离概念。
L0 范数
L0 范数表示向量中非零元素的个数: ∣ ∣ x ∣ ∣ 0 = # ( i ) with x i ≠ 0 ||x||_0 = \#(i) \text{ with } x_i \ne 0 ∣∣x∣∣0=#(i) with xi=0 。
使用 L0 范数的目的就是希望向量的大部分元素都是 0 ,即向量是稀疏的,这样该向量就能在机器学习中用于稀疏编码、特征选择等。通过最小化 L0 范数,来寻找最少最优的稀疏特征项。
但是,L0 范数的最优化问题是一个 NP hard 问题,而且理论上证明了 L1 范数是 L0 范数的最优突近似,所以通常会使用 L1 范数来代替。
L1 范数
L1 范数表示向量中每个元素绝对值的和: ∣ ∣ x ∣ ∣ 1 = Σ i = 1 n ∣ x i ∣ ||x||_1 = \Sigma^n_{i=1}|x_i| ∣∣x∣∣1=Σi=1n∣xi∣ 。L1 范数对应着 L1 距离,即曼哈顿距离(Manhattan Distance)
在机器学习中,使用 L1 正则化的模型叫做 Lasso 回归。L1 正则化可以产生稀疏权值矩阵,即产生一个稀疏模型,可以用于特征选择。
L2 范数
L2 范数表示向量中各元素的平方和然后再求平方根: ∣ ∣ x ∣ ∣ 2 = Σ i = 1 n x i 2 ||x||_2 = \sqrt{\Sigma^n_{i=1}x^2_i} ∣∣x∣∣2=Σi=1nxi2 。L2 范数对应的 L2 距离,即欧式距离(Euclidean Distance)。
在机器学习中,使用 L2 正则化的模型叫做岭回归(Ridge Regression)。L2 正则化可以实现权重衰退,防止模型过拟合。
L1 范数与 L2 范数的对比
L2 范数越小,可以使得权重向量的每个元素都很小,接近于 0 。但 与L1 范数不同的是,L1 会出现等于 0 的值,L2 只会接近于 0。起初 L1 最优化问题解决起来非常困难,因为 L1 范数并没有平滑的函数表示(不可导),但随着计算机技术的发展,很多凸优化算法使得 L1 最优化称为可能。
从贝叶斯先验的角度看,加入正则化相当于加入了一种先验,即当训练一个模型时,仅仅依靠当前的训练数据集是不够的,为了实现更好的泛化能力,往往需要加入先验项。
- L1 范数相当于加入了一个 Laplacean 先验。
- L2 范数相当于加入了一个 Gaussian 先验。
余弦距离
余弦相似度的定义为: ∣ ∣ A − B ∣ ∣ 2 = A ⋅ B ∣ ∣ A ∣ ∣ 2 ∣ ∣ B ∣ ∣ 2 ||A-B||_2 = \frac{A \cdot B}{||A||_2||B||_2} ∣∣A−B∣∣2=∣∣A∣∣2∣∣B∣∣2A⋅B ,取值范围为 [-1, 1]。
用 1 减去余弦相似度即可得到余弦距离:
d
i
s
t
(
A
,
B
)
=
1
−
∣
∣
A
−
B
∣
∣
2
=
1
−
A
⋅
B
∣
∣
A
∣
∣
2
∣
∣
B
∣
∣
2
dist(A, B) = 1 - ||A - B||_2 = 1 - \frac{A \cdot B}{||A||_2||B||_2}
dist(A,B)=1−∣∣A−B∣∣2=1−∣∣A∣∣2∣∣B∣∣2A⋅B
取值范围为 [0, -2]。
需要注意的是,虽然称其为余弦距离,但其并不是严格定义的距离,它满足非负性和对称性,但不满足三角不等式。余弦距离的特点在于,它关注两个向量之间的角度关系,并不关注绝对大小。在电影推荐系统中,不同用户对电影的评分不同,有点评分较低,有点评分较高,用余弦相似度可以排除打分程度的干扰,关注相对差异。可以说 L2 距离体现数值上的绝对差异,余弦距离体现方向上的相对差异。
MSE、RMSE、MAE、R 2 ^2 2
- MSE (Mean Squared Error): 均方误差, P = 1 m Σ ( y i − y ) 2 P = \frac{1}{m}\Sigma(y_i - y)^2 P=m1Σ(yi−y)2
- RMSE(Root Mean Squared Error):均方根误差, P = 1 m Σ ( y i − y ) 2 P = \sqrt{\frac{1}{m}\Sigma(y_i - y)^2} P=m1Σ(yi−y)2
- MAE(Mean Absolute Error):平均绝对误差, P = 1 m Σ ∣ ( y i − y ) ∣ P = \frac{1}{m} \Sigma |(y_i - y)| P=m1Σ∣(yi−y)∣
- R 2 R^2 R2:决定系数, R 2 = 1 − S S r e s S S t o t = 1 − Σ ( y i − y ^ ) 2 Σ ( y i − y ) 2 = 1 − MSE ( y , y ^ ) Var ( y ) R^2 = 1 - \frac{SS_{res}}{SS_{tot}} = 1 - \frac{\Sigma(y_i - \hat{y})^2}{\Sigma(y_i - y)^2} = 1 - \frac{\textbf{MSE}(y, \hat{y})}{\textbf{Var}(y)} R2=1−SStotSSres=1−Σ(yi−y)2Σ(yi−y^)2=1−Var(y)MSE(y,y^)
这些指标主要应用于回归模型。MSE 和 RMSE 可以很好的反映出回归模型预测值与真实值的偏离程度,但如果存在个偏离程度特别大的离群点时,由于使用了平方运算,所以即便离群点的数目非常少,也会使得 MSE 与 RMSE 指标变差。处理这种情况的方法主要有:
- 在数据预处理阶段就把异常点(离群点)过滤掉;
- 提高模型的复杂度,把离群点产生的原因也当做数据特征考虑进去;
- 采用鲁棒性更好的评估指标,如 MAE 等。
准确率、精确率、召回率、F1 值
在定义这四个指标之前,首先要明确 混淆矩阵(Confusion Matrix) 的定义。混淆矩阵通常是一个 2 × 2 的矩阵,行代表模型预测类别的数量统计,列代表数据真实类别标签的数量统计。
| 实际为正类(P) | 实际为负类 (N) | |
|---|---|---|
| 预测为正类(P) | True Positives (TP) | False Positives (FP) |
| 预测为负类(N) | False Negatives (FN) | True Negatives (TN) |
- True Positives : 正确的正样本,即正样本被正确识别为正样本
- False Positives : 错误的正样本,即负样本被错误识别为正样本
- False Negatives : 错误的负样本,即正样本被错误识别为负样本
- True Negatives : 正确的负样本,即负样本被正确识别为负样本
从左上到右下的对角线表示模型预测和数据标签一致的数目,所以对角线之和占总样本数的结果就是准确率。所以我们通常希望对角线越高越好,非对角线越低越好,则说明模型在该类的预测准确率越高。
- 准确率(Accuracy):正确的样本数占总样本数的比例,即 A = T P + T N N A = \frac{TP+TN}{N} A=NTP+TN 。
- 精确率(Precision):预测正确的正类样本数占预测为正类的总样本数的比例,即 P = T P T P + F P P = \frac{TP}{TP+FP} P=TP+FPTP 。
- 召回率(Recall):预测正确的正类样本数占实际为正类的样本总数的比例,即 R = T P T P + F N R = \frac{TP}{TP+FN} R=TP+FNTP 。
- F1 值(F1 score):也称 F 值,精确率和召回率的调和平均值。 F 1 = 2 1 P + 1 R = 2 × P × R P + R F1 = \frac{2}{\frac{1}{P}+\frac{1}{R}} = \frac{2×P×R}{P+R} F1=P1+R12=P+R2×P×R 。
常见的使用场景
- 垃圾邮件过滤:宁可漏掉一些垃圾邮件,也要尽量少将正常邮件识别成垃圾邮件;
- 信息检索:返回足够多的结果供挑选 vs 返回精确结果
不足与调整
准确率、精确率、召回率、F1 值通常用于分类场景。
准确率可以用于表示预测正确的概率,其缺点在于:当数据集中正负类样本比例不平衡时,占大比例的类别会影响模型的准确率。例如,在 异常点检测(Novelty Detection) 中,可能存在 99.99% 都是非异常点,也就是正类,那在验证集或者测试集中,模型容易把所有样本都预测为非异常点,准确率就会非常高。
相比于准确率,精确率和召回率则可以有指定的关注点。精确率关注用户感兴趣的类别,召回率表示用户感兴趣的类别有多少被正确预测出来。通这一对指标一般来说是矛盾的,为了更好的表征模型的精确率和召回率的性能,我们引入了 F1 值。
有些项目领域可能对精确率和召回率的偏重不同,这时就会引入 $ F_{\beta} $ 来表达对两者的不同偏重。
F
β
=
(
1
+
β
2
)
×
P
×
R
(
β
2
×
P
)
+
R
F_{\beta} = \frac{(1+\beta^2) \times P \times R}{(\beta^2 \times P) + R}
Fβ=(β2×P)+R(1+β2)×P×R
其中,当
β
>
1
\beta \gt 1
β>1 时精确率的影响更大,当
β
<
1
\beta \lt 1
β<1 时召回率影响更大。常用
β
=
2
or
0.5
\beta = 2 \text{ or } 0.5
β=2 or 0.5。
P-R 曲线、AP、mAP、ROC 曲线、AUC
P-R 曲线(Precision-recall curve)
采用不同的分类阈值(threshold),则在同一类对象的识别任务中,得到不同的精确率和召回率。横坐标为召回率,纵坐标为精确率的曲线。
通常一个性能好的分类器,它在 recall 增长的同时,precision 也会保持在一个很高的水平;而性能差的分类器,可以能以牺牲 precision 的代价来得到 recall 的提升。从下图可以看出,在不同召回率下,两种算法的精确率表现不同,如果只针对某个点来评估两个模型性能的优劣,则是非常片面的。因此在一些论文当中,作者常常都会使用 PR 曲线,来显示分类器在精确率和召回率之间的权衡,这样才能对模型进行更为全面的评估。

AP 和 mAP
- AP (Average Precision):平均精确度,对不同召回率点上的精确率进行平均,指的就是 P-R 曲线下面部分的面积,通常来说一个分类器性能越好,AP 值越高。
- mAP(Mean Average Precision):多个类别 AP 值的平均值,目标检测算法中最重要的一个指标,大小一定在 [0, 1] 之间,mAP越大,模型性能越好。
ROC 曲线 (Receiver operating characteristic curve)
- 横坐标为假正率(False positive rate,FPR),又称假警报率,表示在所有负样本中被错误预测为正的概率。
- F P R = F P F P + T N FPR = \frac{FP}{FP+TN} FPR=FP+TNFP
- 纵坐标为真正率(True positive rate, TPR), 又称命中率,表示在所有正样本中被正确预测的概率。
- T P R = T P T P + F N TPR = \frac{TP}{TP+FN} TPR=TP+FNTP (相当于召回率)
通常 ROC 曲线的横纵坐标都是取值在 [0, 1] 之间,当我们每取一个不同的阈值时,就可以得到一组(FPR, TPR),即ROC 曲线上的一个点。ROC 曲线有以下的一些特性:
- 曲线位置越靠近左上角,分类器性能越好;
- 当数据集中的正负样本分布发生变化时,ROC 曲线基本能保持不变。
- 当阈值的取值数量足够多时,得到的 ROC 曲线是光滑的,那么基本可以判断该分类器没有太大的过拟合(overfitting)。
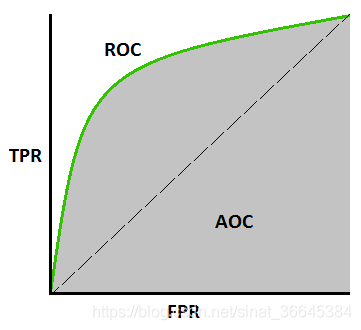
AUC (Area under curve)
ROC 的曲线下面积,它是一个概率值,表示当你随机挑选一个正样本以及一个负样本时,当前分类算法根据 score 值将这个正样本排在负样本前面的概率就是 AUC 值。因此,AUC 越大,越接近于 1,分类器的性能则越好,也就是讲正样本排在负样本前面的概率更好,能实现更好的分类。由于 ROC 通常在直线 y = x 上面,所以 AUC 的值都在 [0.5, 1] 之间。
优缺点比较
| 曲线 | P-R 曲线 | ROC 曲线 |
|---|---|---|
| 优点 | 精确率和召回率都聚焦于正类,当类别分布不平衡的数据集倾向于正类时,P-R 曲线则被广泛认为优于 ROC 曲线。 | 当数据集正负样本的分布发生变化的时候,ROC 曲线能够保持不变,TPR 聚焦于正类,FPR 聚焦于负类,使得评估相对比较均衡。 |
| 缺点 | 在实际环境中,正负样本的分布常常会发生变化,或者分布比例非常不平衡,这个时候 P-R 曲线就会发生明显的变化。 | 在类别不平衡的背景下(如主要关心正类的信息检索过程),负类增加了很多,大量负类被预测为正类,但曲线没有变化,这就相当于提升了大量的 FP,此时 FPR 却没有明显增长,导致 ROC 曲线呈现一个过分乐观的评估效果。 |
| 使用场景 | 1. 测试不同类别分布下分类器的性能和影响; 2. 评估在相同类别分布下正类的预测情况 | 1. 评估分类器的整体性能; 2. 单纯比较分类器的性能,且排除类别不平衡对分类造成的影响 |
总的来说,在实际环境中类别不平衡的情况居多,由于 ROC 通常会给出一个乐观的估计效果,所以 P-R 曲线的使用更为广泛。
IoU、NMS
这几个评估指标通常使用与目标检测的任务当中。
IoU (Intersection over Union)
IoU 指的是模型预测的 bounding-box 和 GroundTruth 之间的交并比,可以理解为模型预测出来的框与数据集中标记的框的重合程度,作为检测的准确率。
IoU
=
D
e
t
e
c
t
i
o
n
R
e
s
u
l
t
∩
G
r
o
u
n
d
T
r
u
t
h
D
e
t
e
c
t
i
o
n
R
e
s
u
l
t
∪
G
r
o
u
n
d
T
r
u
t
h
\textbf{IoU} = \frac{Detection Result \cap GroundTruth}{Detection Result \cup GroundTruth}
IoU=DetectionResult∪GroundTruthDetectionResult∩GroundTruth
NMS(Non-Maximum Suppression)
NMS 为非极大值抑制。因为在目标检测中,对于同一个物体,模型常常会预测出多个 bounding box,所以 NMS 就要去除多余的预测框,只保留和 ground truth 重叠度最高的预测框。
在目标检测中,分类器会给每个 bounding box 计算出一个 class score,也就是这个预测框属于每一类的概率。根据 score 矩阵和 region 的坐标信息,从中找出置信度比较高的 bounding box。对于存在重叠部分的预测框,只保留得分最高的那个。NMS 一次处理一个对象类别,如果数据集中有 N 个类别,则 NMS 要执行 N 次。具体的操作过程为:
- 对于每一类,先把所有 score 小于设定阈值的预测框的 score 设为 0;
- 根据 bounding box 的 score 进行排序,把 score 最大的 bounding box 作为队列中首个进行比较的对象;
- 计算其余 bounding-box 与当前 score 最大的 bounding-box 的 IoU,去除 IoU 大于设定阈值的预测框,保留 IoU 较小的那些预测框。
- 在未处理的 bounding box中继续重复上述过程,直到所有的预测框都被使用。
可以看出,在上面过程中存在两个关键的阈值:IoU 阈值和 score 阈值。