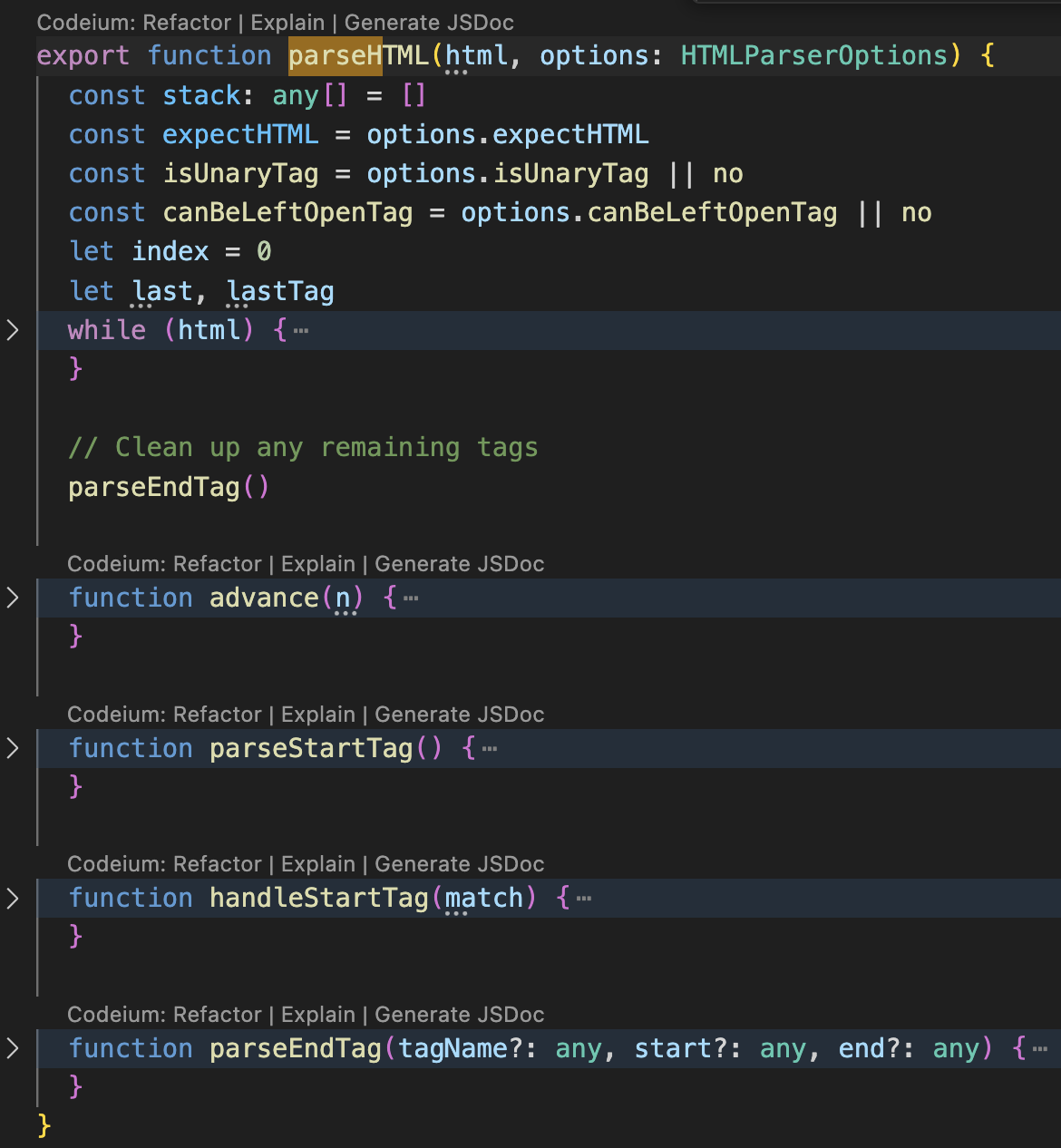
单调队列优化DP
- AcWing 135. 最大子序和
- AcWing 1087. 修剪草坪
- AcWing 1089. 烽火传递
- AcWing 1090. 绿色通道
关于单调队列的初始化

AcWing 135. 最大子序和
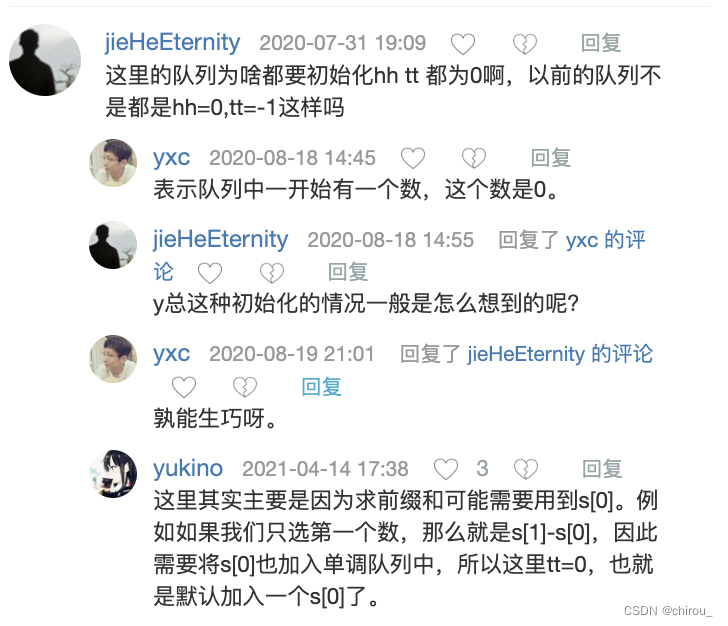
注意hh = 0,tt = -1 tt = 0初始化的时候队列有什么不同,主要还是要理解队列的实际意义
#include <iostream>
using namespace std;
typedef long long LL;
const int N = 3 * 1e5 + 10;
int q[N];
LL s[N];
int n, m;
int main()
{
cin >> n >> m;
//预处理前缀和数组
for (int i = 1; i <= n; ++ i)
{
cin >> s[i];
s[i] += s[i - 1];
}
LL res = -1e9;//不能初始化为0,因为s[]可能小于0
//维护单调队列
//如果不把s[0]先放进来,res一开始就会置为0,这在负数的时候不正确
//比如这个样例:
//6 4
//-1 -3 -5 -1 -2 -3
//但是如果这么写就可以了 if (i != 0) res = max(res, s[i] - s[q[hh]]);
// int hh = 0, tt = -1;
// //q[++tt] = 0;//先把s[0]放进来
// for (int i = 0; i <= n; ++ i)
// {
// if (hh <= tt && i - q[hh] > m) hh ++;
// res = max(res, s[i] - s[q[hh]]);
// while (hh <= tt && s[i] <= s[q[tt]]) tt --;
// q[++tt] = i;
// }
int hh = 0, tt = -1;
q[++tt] = 0;//先把s[0]放进来
for (int i = 1; i <= n; ++ i)//s[0]已经放进去了,从1开始就行了
{
if (hh <= tt && i - q[hh] > m) hh ++;
res = max(res, s[i] - s[q[hh]]);
while (hh <= tt && s[i] <= s[q[tt]]) tt --;
q[++tt] = i;
}
cout << res;
return 0;
}
AcWing 1087. 修剪草坪
#include <iostream>
using namespace std;
const int N = 1e5 + 10;
typedef long long LL;
LL f[N];//从1到i,不选第i个的最小损失的效率
int q[N];
int n, m;
LL res = 1e18 + 7, ans = 0;//res要开到1e18 + 7,开小了过不了
int main()
{
cin >> n >> m;
for (int i = 1; i <= n; ++ i)
{
cin >> f[i];//在这里我们直接用f[i]来存一下数据,这样可以少开一个数组
ans += f[i];
}
int hh = 0, tt = 0;//相当于默认吧s[0] = 0放进去了
for (int i = 1; i <= n; ++ i)
{
if (hh <= tt && i - q[hh] > m + 1) hh ++;//不能连续选m个,转化为每m+1个必须选一个不选,
f[i] += f[q[hh]];//在队列长度还没到m+1之前,q[hh] = 0,f[q[hh] 也是 0,
//当i-q[hh]达到m+1时就会每次循环叠加一个f[q[hh]],保证每m+1头牛有一头不选的同时损失的效率最小
while (hh <= tt && f[i] <= f[q[tt]]) tt --;//经过上一步叠加后,f[i]已经不是之前的f[i]了,
//如果此时叠加后的f[i]比队尾维护的损失效率更小,那么队尾的数据没用了,直接出队
q[++tt] = i;//不能是tt++,因为一开始q[hh]是0,如果tt++会用1覆盖掉最初的q[hh]
}
for (int i = n - m; i <= n; ++ i)//n-m ~ n是m + 1头牛,我们经过上一个完整的for循环后此时的f[i]就是我们定义的:从1到i,不选第i个的最小损失的效率
{ //最后m+1头牛中我们选择一头不选就行了,不需要res+=是因为此时的f[i]经过我们的预处理已经是叠加后的值
res = min(res, f[i]);
}
cout << ans - res;
return 0;
}
AcWing 1089. 烽火传递

#include <iostream>
typedef long long LL;
using namespace std;
const int N = 1e6 + 10;
LL s[2 * N];//计算每个点加油量- 耗油量的前缀和,如果s[j] - s[i] < 0;说明从i到j亏油了,不能从i到j,
//我们要找的就是i ~ i+n-1或者i-(n-1) ~ i这个区间里是否有最小的s[j]使得s[j]-s[i]>=0,如果最小的都>=0那么这个区间内的其他地点肯定也可以顺利到达
//如何找一个区间内最小的s[j]呢,这就用到了单调队列,我们维护一个区间的单调队列s[q[hh]]就是这个区间内最小的s[j]
int mark[N], q[N * 2], oli[N], d[N];
int n;
int main()
{
cin >> n;
for (int i = 1; i <= n; ++ i) cin >> oli[i] >> d[i];
//顺时针游行
for(int i = 1;i <= n;i ++) s[i] = s[i + n] = oli[i] - d[i];//表示i地点加的油和到下一地点消耗的油的差
for (int i = 1; i <= 2 * n; ++ i) s[i] += s[i - 1];//顺时针游行的时候是从1到n,这个游行顺序的话我们前缀和也是给后面的加上前面的数列之和
/*
顺时针游行从大到小遍历的原因:
比如计算到i=6这个点时,需要的数据是6~13这个区间内的的前缀和,从6~13这个区间内找一个最小的s[j] - s[6]看是否满足>=0
如果从小到大遍历,那么队列中并不会存在6~13这个区间内的前缀和,存在的是从-1~6这个区间的前缀和
所以要从大到小进行枚举遍历
*/
int hh = 0, tt = -1;
for (int i = 2 * n; i >= 1; -- i)
{
if (hh <= tt && q[hh] > i + (n - 1)) hh ++;//从i到q[hh]这个地点总地点数超过了n(包括i和q[hh]这两个地方)
while (hh <= tt && s[q[tt]] >= s[i]) tt --;
q[++ tt] = i;
//因为我们是环绕一圈,起点是i终点也是i,所以队列里要包含i这个点,所以添加完i入队后我们再if判断是否合法
if (i <= n && s[q[hh]] - s[i - 1] >= 0) mark[i] = 1;//因为我们计算s[i]的时候根据题意是当前点的加油量-到下一地点的蚝油量,所以这里-s[i - 1]就行了
}
//逆时针游行
hh = 0, tt = -1;
d[0] = d[n];s[1]计算的时候需要
for(int i = 1;i <= n;i ++) s[i] = s[i + n] = oli[i] - d[i - 1];//逆时针反正开,所以s[i]应该是当前点的加油量-当前点到前面点的距离
for (int i = 2 * n; i >= 1; -- i) s[i] += s[i + 1]; //逆时针游行的时候是从n到1,这个游行顺序的话我们前缀和是给前面的加上后面的数列之
for (int i = 1; i <= 2 * n; ++ i)//逆时针的时候我们需要的s是s[1]~s[n],顺时针的时候是s[n]~s[2 * n]
{
//注意这里是q[hh] < 不是 >,因为逆时针的时候目的地在出发地的前面
if (hh <= tt && q[hh] < i - (n - 1)) hh ++;//从i到q[hh]这个地点总地点数超过了n(包括i和q[hh]这两个地方)
while (hh <= tt && s[q[tt]] >= s[i]) tt --;
q[++ tt] = i;
//因为我们是环绕一圈,起点是i终点也是i,所以队列里要包含i这个点,所以添加完i入队后我们再if判断是否合法
if (i >= n && s[q[hh]] - s[i + 1] >= 0) mark[i - n] = 1;//因为我们计算s[i]的时候根据题意是当前点的加油量-到下一地点的蚝油量,
//但是我们是逆时针游行,所以我们的上一个地点的下标其实是i+1所以这里-s[i + 1]就行了
}
for (int i = 1; i <= n; ++ i)
{
if (mark[i]) cout << "TAK" << endl;
else cout << "NIE" << endl;
}
return 0;
}
#include<iostream>
using namespace std;
const int N = 2 * 1e5 + 10;
int w[N], q[N];
int f[N];//表示以i为右端点的前缀区间,并且点燃i烽火台的总代价最小是多少
int n, m;
int main()
{
cin >> n >> m;
for (int i = 1; i <= n; ++ i) cin >> w[i];
int hh = 0, tt = 0;
for (int i = 1; i <= n; ++ i)
{
if (hh <= tt && i > q[hh] + m) hh ++;//保证队列里面就m个
f[i] = f[q[hh]] + w[i];
while (hh <= tt && f[q[tt]] >= f[i]) tt --;
q[++tt] = i;
}
if (hh <= tt && (n + 1) > q[hh] + m) hh ++ ;//将队列的右端点移动到n+1的位置(即点燃了第n+1个烽火台),说明在n+1这个虚拟的烽火台的前面的n个烽火台都已经可以沟通了
//在这个区间中找一个f[i]既符合题意:可以使n个烽火台进行交流
//也可以直接用f[q[hh]]找到这个区间内最小的总代价
//因为w[n+1]默认是0,所以点染它没有代价
cout << f[q[hh]];
return 0;
}
AcWing 1090. 绿色通道
这题的队列长度最小值(最少空几题)是我们自己不断二分试出来的,二分判断的性质就是如果为了空limit题至少需要多少分钟去写题目,看看这个时间有没有超过题目给的时间,没超过题目给的时间就是合法的
#include <iostream>
using namespace std;
const int N = 5 * 1e4 + 10;// == 5e4 + 10
int f[N];//表示以i为右端点的前缀区间,并且写第i题后一共花费多少时间
int w[N], q[N];
int n, m;
bool check(int limit)
{
int hh = 0, tt = 0;
for (int i = 1; i <= n; ++ i)
{
if (hh <= tt && i > q[hh] + limit + 1) hh ++;
f[i] = f[q[hh]] + w[i];//q[hh]是上一个写作业的地方
while (hh <= tt && f[q[tt]] >= f[i]) tt --;
q[++tt] = i;
}
if (n + 1 > q[hh] + limit + 1) hh ++;
return f[q[hh]] <= m;//类似上一题烽火那题
}
int main()
{
cin >> n >> m;
for (int i = 1; i <= n; ++ i) cin >> w[i];
int l = 0, r = n;
while (l < r)
{
int mid = l + r >> 1;
if (check(mid)) r = mid;//求的是最小的mid,因此往左边二分
else l = mid + 1;
}
cout << r;
return 0;
}