- 练习1
给你n个整数,每个数可选或不选,要求选一些数,使它们的和为S,问有多少种方案?
输入格式
第一行:2个整数n和s,范围都在[1, 100]。
第二行:n个整数,每个数范围在[-100, 100]。
输出格式
输出方案数。(答案不超过2^63)
输入/输出例子1
输入:
6 10
3 4 7 8 -1 2
输出:
4
样例解释:
3+7, 3+8-1, 4+7-1, 8+2
样例解释
无
代码奉上
#include<bits/stdc++.h>
using namespace std;
int n,s,d[10011];
long long f[10001];
int main(){
cin>>n>>s;
for(int i = 1;i <= n;i++){
cin>>d[i];
}
sort(d+1,d+n+1);
int m=n+1;
for(int i = 1;i <= n;i++){
if(d[i]>= 0){
m = i;
break;
}
}
f[0] = 1;
for(int i = m;i <= n;i++){
for(int j = 10000;j >= 0;j--){
if(f[j] != 0&&(j+d[i]<= 10000)){
f[j+d[i]]+=f[j];
}
}
}
for(int i = 1;i < m;i++){
for(int j = 0;j <=10000;j++){
if(f[j] != 0&&(j+d[i]>= 0)){
f[j+d[i]]+=f[j];
}
}
}
cout<<f[s];
return 0;
}给你n个正整数,要求你分成2堆,使它们各自的和尽量相同。问2堆的差距最小是多少?
输入格式
第一行:1个整数n,范围都在[1, 1000]。
第二行:n个整数,每个数范围在[1, 100]。
输出格式
输出最小差距。
输入/输出例子1
输入:
6
3 4 7 8 1 2
输出:
1
样例解释:
13=3+7+1+2
12=4+8
样例解释
无
代码:
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
const int MAX_N = 1005;
const int MAX_SUM = 50005;
int main() {
int n;
cin >> n;
vector<int> nums(n);
int sum = 0;
for (int i = 0; i < n; i++) {
cin >> nums[i];
sum += nums[i];
}
int half_sum = sum / 2;
vector<bool> dp(MAX_SUM, false);
dp[0] = true;
for (int i = 0; i < n; i++) {
for (int j = half_sum; j >= nums[i]; j--) {
if (dp[j - nums[i]]) {
dp[j] = true;
}
}
}
int min_diff = sum;
for (int j = half_sum; j >= 0; j--) {
if (dp[j]) {
min_diff = sum - 2 * j;
break;
}
}
cout << min_diff << endl;
return 0;
}给你n个正整数,每个数可选或不选,要求选一些数,使它们的和为S,输出任意一种方案。
输入格式
第一行:2个整数n和s,范围都在[1, 10000]。
第二行:n个整数,每个数范围在[1, 1000]。
输出格式
输出任意一种方案。如果没有方案,输出-1。
输入/输出例子1
输入:
6 110
30 50 100 70 30 40
输出:
30 50 30
样例解释:
或者 70 40也可以。
样例解释
无
代码:
#include<bits/stdc++.h>
using namespace std;
long long n,a,s;
long long fa[1000005],b[1000005];
int main()
{
cin>>n>>s;
b[0]=1;
for(int i=1;i<=n;i++){
cin>>a;
if(a>s)continue;
for(int j=s;j>=0;j--)
{
if(b[j]!=0&&!fa[j+a])
{
b[j+a]++;
fa[j+a]=a;
}
}
}
if(b[s]==0)
{
cout<<-1;
return 0;
}
while(s!=0)
{
cout<<fa[s]<<" ";
s-=fa[s];
}
return 0;
}
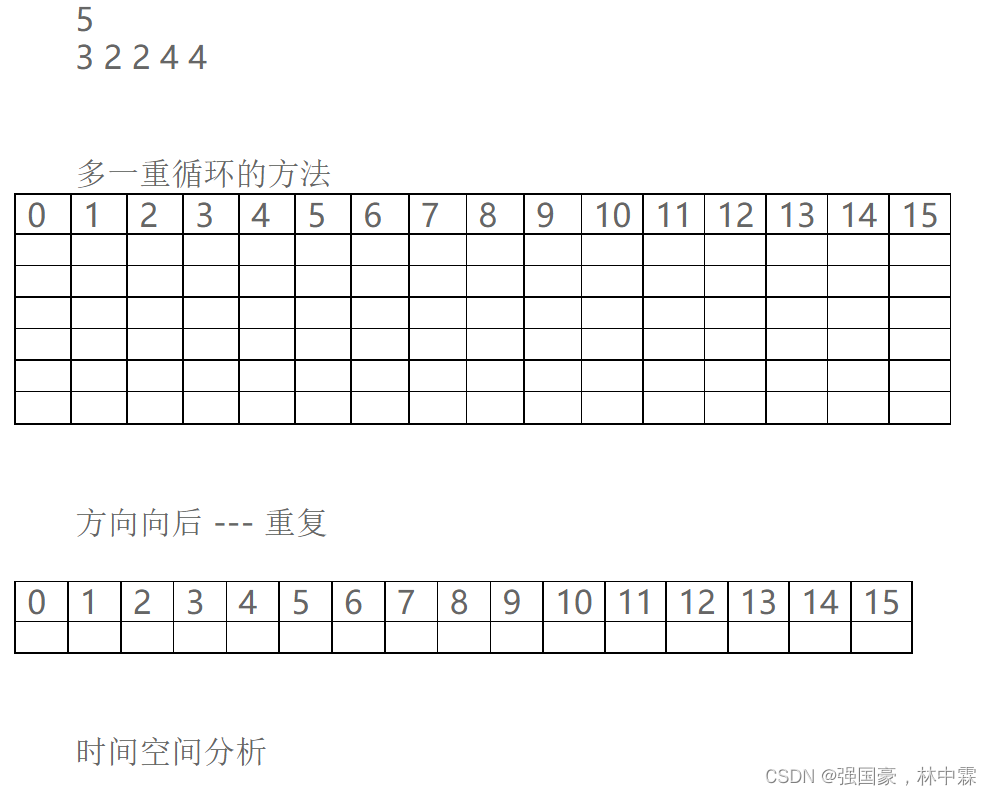
- 练习2
给出储钱罐的重量,每种钱对应的重量和价值,求出储钱罐内至少有多少钱?
输入格式
第一行为一个正整数T,表示T(T<=5)组测试数据。
每组数据:
第一行为两个正整数E,F(1<=E<=F<=10000),表示空的储钱罐的重量和装了钱后的重量。
第二行为一个正整数N(1<=N<=500),表示钱的种类数。
接着的N行每一行有两个正整数P,W(1<=P<=50000, 1<=W<=10000),表示钱的价值与重量。
输出格式
每组测试数据一行一个句子“The minimum amount of money in the piggy-bank is X.”X为至少有多少钱,如果无解,则输出“This is impossible.”(注意有英文句号)
输入/输出例子1
输入:
3
10 110
2
1 1
30 50
10 110
2
1 1
50 30
1 6
2
10 3
20 4
输出:
The minimum amount of money in the piggy-bank is 60.
The minimum amount of money in the piggy-bank is 100.
This is impossible.
样例解释
无
代码
#include <iostream>
#include <vector>
#include <limits>
int findMinimumAmount(int E, int F, int N, std::vector<std::pair<int, int> >& coins) {
std::vector<int> dp(F + 1, std::numeric_limits<int>::max());
dp[0] = 0;
for (int j = 0; j < N; j++) {
for (int i = 1; i <= F; i++) {
if (i >= coins[j].second && dp[i - coins[j].second] != std::numeric_limits<int>::max()) {
dp[i] = std::min(dp[i], dp[i - coins[j].second] + coins[j].first);
}
}
}
return (dp[F-E] != std::numeric_limits<int>::max()) ? dp[F-E] : -1;
}
int main() {
int T;
std::cin >> T;
while (T--) {
int E, F;
std::cin >> E >> F;
int N;
std::cin >> N;
std::vector<std::pair<int, int> > coins(N);
for (int i = 0; i < N; i++) {
std::cin >> coins[i].first >> coins[i].second;
}
int result = findMinimumAmount(E, F, N, coins);
if (result != -1) {
std::cout << "The minimum amount of money in the piggy-bank is " << result << "." << std::endl;
} else {
std::cout << "This is impossible." << std::endl;
}
}
return 0;
}
- 练习3
给出N种钱币的面值和每种钱币的个数,问要凑出M的钱最少要用多少枚钱币?
例如:N=4,M=40,钱币面值分别为:3,6,8,9 , 个数分别是:10,10,2,1。
答案为:6。
输入格式
第一行:2个整数N和M,N范围在[1,50],M范围在[1,1000000]。
第二行:N个整数表示每种钱币的面值,每个数范围在[1,100]。
第三行:N个整数表示每种钱币的数量,每个数范围在[1,100000]。
输出格式
输出最少钱币数。 输出最少钱币数。如果没有方案,输出-1。
输入/输出例子1
输入:
2 100
5 8
20 6
输出:
17
样例解释
无
代码:
#include<bits/stdc++.h>
using namespace std;
int N,M,d[510],c[510],ans = 0;
int nn,dd[10000],cc[10000];
int f[10000006];
int main(){
cin>>N>>M;
for(int i = 1;i <= N;i++){
cin>>d[i];
}
for(int i = 1;i <= N;i++){
cin>>c[i];
if(c[i]>M/d[i]){
c[i] = M/d[i];
}
}
nn = 0;
for(int i = 1;i <= N;i++){
int x = c[i];
for(int p2 = 1;x > p2;p2*=2){
dd[++nn] = p2*d[i];
cc[nn] = p2;
x -= p2;
}
if(x > 0){
dd[++nn] = x*d[i];
cc[nn] = x;
}
}
f[0] = 1;
for(int i = 1;i <= nn;i++){
for(int j = M-dd[i];j >= 0;j--){
if(f[j]>0){
if(f[j+dd[i]] == 0|| f[j+dd[i]]>f[j]+cc[i]){
f[j+dd[i]] = f[j]+cc[i];
}
}
}
}
ans = f[M]-1;
cout<<ans;
return 0;
}