---

摘要

This week, I read an computer science about a deep learning repair method for atmospheric environmental quality data based on Gaussian diffusion. Since deviation or missing atmospheric environmental data will greatly affect regional atmospheric quality analysis, this paper proposes a deep learning repair method based on Gaussian diffusion and gate cycle unit, GD-GRU, to improve the accuracy of atmospheric environmental data repair. The inputs are meteorological parameters and pollutant parameters, and the errors of estimates and observations are used as GRU outputs to calculate the missing data. The experimental analysis shows that the GD-GRU model has good performance and is superior to other models on average when applied to the repair of long sequence missing data. In addition, I continue to learn the relevant knowledge of NS equations and the possibility of thinking about the combination of NS equations and deep learning, using deep learning to optimize PDE solutions.

本周，阅读了一篇基于高斯扩散的大气环境质量数据深度学习修复方法的文章。由于大气环境数据出现偏差或缺失会对区域大气质量分析造成很大影响，对此文章提出了一种基于高斯扩散和门循环单元的深度学习修复方法，GD-GRU，旨在提高大气环境数据修复精度。输入为气象参数和污染物参数，估计值和观测值的误差作为GRU的输出，以此计算缺失数据。通过实验分析显示，将GD-GRU模型应用到长序列缺失数据的修复中，表现出良好的性能，并且平均优于其他模型。此外，我继续学习了NS方程的相关知识，以及思考NS方程与深度学习结合的可能性，即用深度学习优化PDE求解。

---

文献阅读

1.题目

文献链接：A deep learning method to repair atmospheric environmental quality data based on Gaussian diffusion

2.问题

1）在理想条件下，由于参数的默认和缺乏，物理模型处理非线性问题存在局限性。
2）虽然非线性机器学习模型可以提高预测精度，但它不能增强时间序列数据的时间滞后或长期学习依赖性。
3）虽然RNN等深度学习模型可以提高预测精度，但它是用既定数据训练的，因此无法预测没有历史数据集的极值。

3.解决方案

1）通过物理模型和深度学习模型提高模型训练的准确性，但为了有效修复空气质量数据，必须限制极值的预测精度。
2）建立了一个高斯扩散和门循环单元的耦合模型(GD-GRU)，以提高数据修复的准确性。
3）利用深度学习和物理模型对极值进行高精度仿真和预测，可以解决物理模型参数监测和机器学习模型训练不足的问题。

4.方法

4.1 框架

组成部分：数据收集、高斯扩散、误差修正模型、结果分析和应用。
研究数据：桂林市各监测站的站点数据和空气质量数据

4.2 基于高斯扩散的修复方法

1)使用Pearson系数来计算站间的相关性，分析台站间PM2.5的相关强度。

表中数据显示，具有显著相关性的台站主要位于目标台站的逆风位置，这些区域容易形成湍流，不利于PM2.5扩散。
2）高斯扩散模型：

其中：X(X, y, z, t, H)为下风X米、横向y米、离地面z米;σx、σy、σz分别是根据大气稳定性选择参数计算的x、y、z轴上的扩散参数;H为监测点高度;u为平均风速。

均方根误差：

4.3 PM2.5的误差校正模型

1）目标：根据过去几个小时的PM2.5误差、天气和污染物来预测未来几个小时的PM2.5误差。于是将参数矩阵化：

误差修正模型采用GRU神经网络建立，其中f(⋅)为训练函数。上式可重写为:

2）GRU的结构：

3）计算公式：

GRU很好地捕捉了长期相关性，可以记住长时间内空气质量的周期性模式。

4.4 PM2.5数据修复的GD-GRU模型

GD-GRU模型结构示意图：

输入输出均为连续时间序列，利用PM2.5估计值和PM2.5误差计算预测PM2.5。

4.5 评估指标

采用MAE、RMSE和SMAPE三个评价指标评价GD-GRU的预测性能：

其中：n为样本总数，yi为实测时间序列，yi′为预测时间序列。

5.实验

5.1 网络参数

1）通过实验数据显示，神经元数目为64个，时间步长为10个时，效率最高，更有利于建模。

2）采用自相关函数分析PM2.5浓度时间序列之间的时间相关性：

3）随着时间步长的增加，较早的事件受当前状态的影响较小，呈明显的下降趋势。当时间步长小于9时，自相关系数大于0.8，具有较高的时间相关性。因此，将时间步长设置为10。

5.2 实验结果

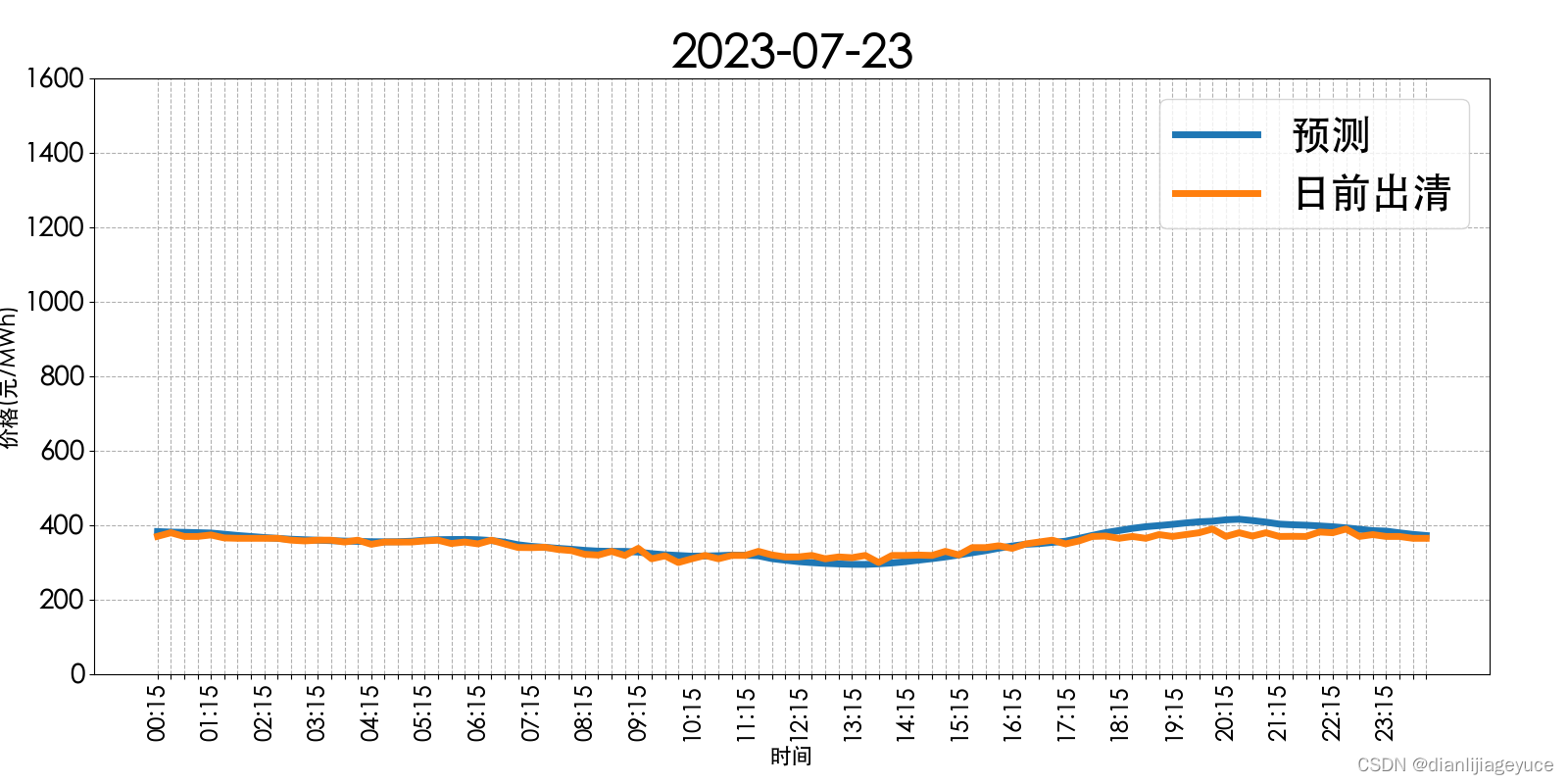
1）预测表现

在整个预测范围内，GD-GRU预测性能很准确。即使在污染数据突然变化的情况下，GD-GRU也能表现出良好的性能。因此，实验结果表明所建立的模型可以在不同情况下修复数据。

2）高斯扩散对预测性能的影响

实验结果表明，高斯扩散模型与GRU具有相似的性能，GD-GRU保证了基于物理规律的预测趋势与实际趋势更加一致。

3）GD-GRU与其他方法的比较

与其它模型相比，GD-GRU对污染物的局部急剧变化更为敏感，这主要是因为高斯扩散模型能够获得更丰富的局部变化信息。GD-GRU可以修复自动在线监测站的污染物数据，并为改善人类健康提供许多有用的信息。

6.结论

1）为了修复偏差和缺失的大气环境监测数据，文章提出了一种基于高斯扩散法和神经网络耦合的大气污染数据修复模型。
2）训练数据集由气象、污染物参数和均方根误差数据的一组序列数据构建，其中均方根误差数据由高斯扩散模型的观测值和预测值计算得到。
3）实验结果表明，GD-GRU模型的预测效果优于高斯扩散模型和GRU模型，能够有效修复大气污染数据。
4）GD-GRU模型的优势是在一些极端情况下，可以计算出物理过程的极值，并使误差函数最小化，使数据恢复的趋势仍然符合大气污染物传播的自然规律。

7.展望

1）文章忽略了不同湍流风向在微观尺度上的物理效应，因此在未来每个点独立建模，用于风向分析的落后气团轨迹模型被小尺度湍流模型取代。
2）GD-GRU模型只能解决PM2.5在特定尺度条件下按照物理规律的传输和数据恢复问题，因为PM2.5受到化学变化、地理等诸多因素的影响。
3）在PM2.5扩散分析中考虑化学变化过程和地理因素，可以将误差限制在非常小的范围内，利用深度学习模型解决误差修正，达到更高的精度。

Ns方程

1.NS方程每一项的物理意义

其中：
1）公式左边：时间项，对流项；
2）公式右边：压力项，体积力和粘性力。

2.NS方程的推导过程

1）动量方程

其中：P是动量；V是一个关于xyzt的速度表达式，即是一个向量；u,v,w是V在xyz方向上的速度分量。

2）作用在流体粒子上的力

图中表示作用在流体粒子的力，对于一个流体粒子的中心来说，它会受到应力和剪切力，即类似压强，乘以面积后就是力。

3）微分动量方程
汇总动量方程和作用在流体粒子的力之后，可以得到下面的方程：

4）Navier Stokes方程
应力和剪切力的公式为：

其中：p是局部热力学压力

当应用于具有恒定粘度的不可压缩的流体时，方程大大简化，就得到了常见的NS方程：

3.深度学习与NS方程

PDE求解方法分为两种：
1）传统方法：有限元和有限微分
有限元：粗糙分辨率网格必然快且不准，而精细分辨率网格必然慢但是精准；计算的时候，需要做网格无关性验证，即网格增加一倍后，精度不变；网格过少，得不到准确结果的；网格过多，也无意义，甚至有副作用。
2）数据驱动
Finite-dimensional operators：神经网络参数化一个有限维的算子，输入和输出都是有限维的欧几里得空间；这些方法依赖于网格，并且需要针对不同的分辨率和离散化进行修改和调整，以实现一致的误差。
Neural-FEM：使用一组有限的基函数来参数化特定条件下方程的解

4.PINNs模型

PINNs模型是AI在偏微分方程领域应用中的模型，只需要初边值条件和方程即可求解，并且在精度上具有超越数值方法的潜力。

以Burgers方程为例：

使用初边界条件做约束，直接计算模型的输出在初始和边界时和条件的MSE：

PINNs模型的亮点在于计算方程的Loss，当输出的u和对应的导数满足方程时，f是等于0的。因此，目标是让f尽可能的接近0。这样就实现了即使不知道真值u，也能计算出方程的Loss用于指导神经网络参数的更新，实现了非监督学习的效果。

写成MSE的形式：

而二者的权重分配，分别采用了定值和动态调整的策略：

5.NS方程描述污染物的运动

1）确定初始条件和边界条件
初始条件描述了在t=0时刻的流体速度和污染物浓度分布，而边界条件反映了流体速度和污染物浓度在流体区域边界的行为。
2）数值求解
一般情况下，NS方程是非线性的偏微分方程，很难找到解析解。因此，考虑使用有限元法求解这些方程的数值解，可以在计算机上进行模拟，得到流体速度场和污染物浓度场随时间和空间的变化。
3）预测污染物运动
通过这样的模拟，可以了解污染物在流体中的传输过程，预测污染物的扩散范围，以及对不同条件下的污染物传输行为进行研究。

---

总结

本周，我学习了NS方程的相关知识，以及思考NS方程与深度学习结合的可能性。下周，我将继续补充学习NS方程的理论知识，怎么用NS方程表述污染物的运动，继续思考怎么将NS方程与深度学习结合起来。