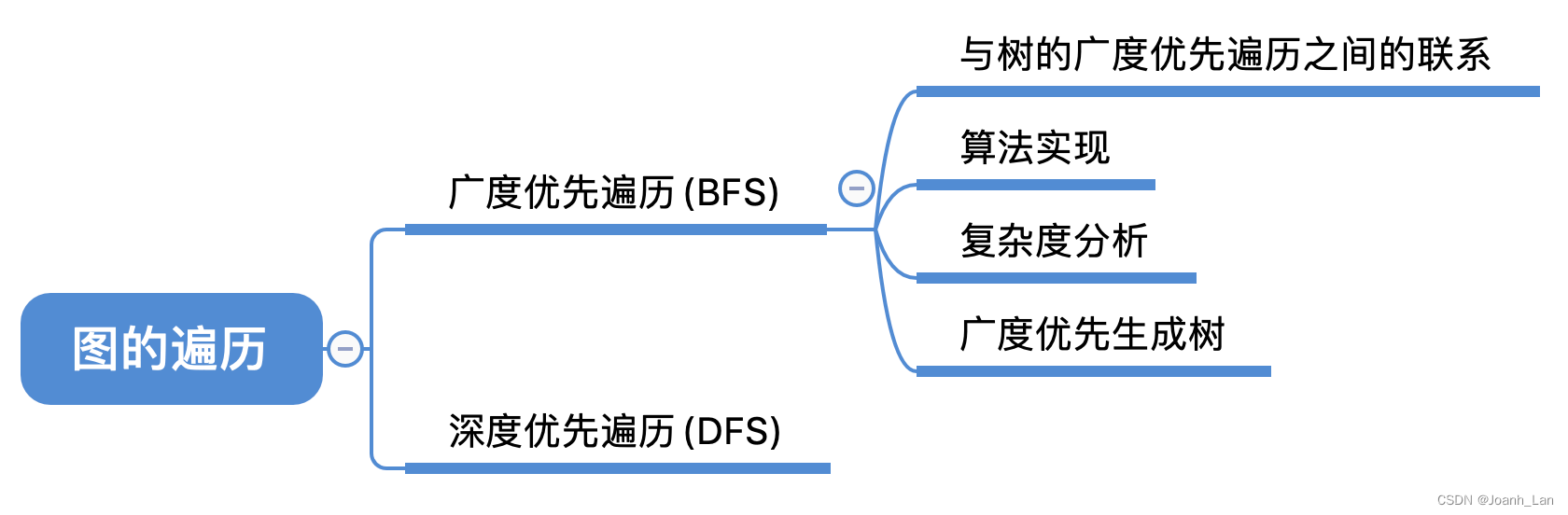
数据结构–图的遍历 BFS
树的广度优先遍历
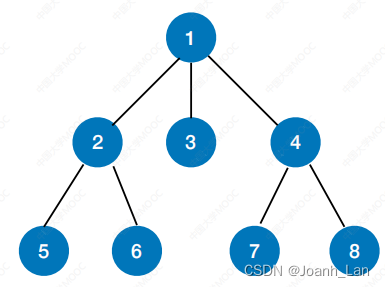
从 1 结点进行
b
f
s
bfs
bfs的顺序:
【1】
【2】【3】【4】
【4】【6】【7】【8】
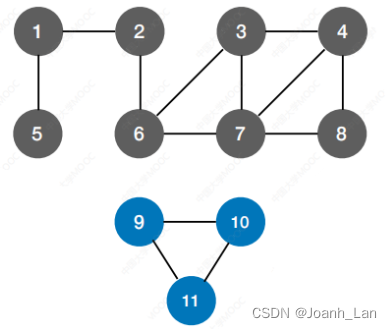
图的广度优先遍历
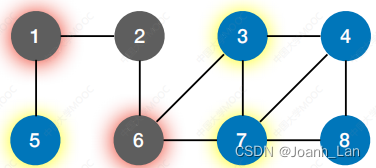
从 2 号点开始
b
f
s
bfs
bfs的顺序:
【2】
【1】【6】
【5】【3】【7】
【4】【8】
树 vs 图
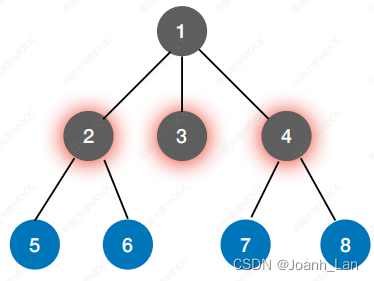
不存在“回路”,搜索相邻的结点时,不可能搜到已经访问过的结点
树的⼴度优先遍历(层序遍历):
①若树⾮空,则根节点⼊队
②若队列⾮空,队头元素出队并访问,同时将该元素的孩⼦依次⼊队
③重复②直到队列为空

搜索相邻的顶点时,有可能搜到已经访问过的顶点
代码实现
⼴度优先遍历(Breadth-First-Search, BFS)要点:
- 找到与⼀个顶点相邻的所有顶点
- 标记哪些顶点被访问过
- 需要⼀个辅助队列
•FirstNeighbor(G,x):求图G中顶点x的第⼀个邻接点,若有则返回顶点号。
若x没有邻接点或图中不存在x,则返回-1。
•NextNeighbor(G,x,y):假设图G中顶点y是顶点x的⼀个邻接点,返回除y之外
顶点x的下⼀个邻接点的顶点号,若y是x的最后⼀个邻接点,则返回-1
bool visited[MAX_VERTEX_NUM];
//广度优先遍历
void BFS(Graph G, int v)
{
//从顶点v出发,广度优先遍历图G
visit(v);
//访问初始顶点v
visited[v] = TRUE;
//对v做已访问标记
Enqueue(Q, v);
//顶点v入队列Q
while(!isEmpty(Q))
{
DeQueue(Q, v);
//顶点v出队列
for(w = FirstNeighbor(G, v); w >= 0; w = NextNeighbor(G, v, w)) //检测v所有邻接点
if(!visited[w]) //w为v的尚未访问的邻接顶点visit(w);//访问顶点W
{
visited[w] = TRUE; //对w做已访问标记EnQueue(Q,w); //顶点w入队列
}//if
}//while
}
遍历序列的可变性

同⼀个图的邻接矩阵表示⽅式唯⼀,因此⼴度优先遍历序列唯⼀ \color{red}同⼀个图的邻接矩阵表示⽅式唯⼀,因此⼴度优先遍历序列唯⼀ 同⼀个图的邻接矩阵表示⽅式唯⼀,因此⼴度优先遍历序列唯⼀
同⼀个图邻接表表示⽅式不唯⼀,因此⼴度优先遍历序列不唯⼀ \color{red}同⼀个图邻接表表示⽅式不唯⼀,因此⼴度优先遍历序列不唯⼀ 同⼀个图邻接表表示⽅式不唯⼀,因此⼴度优先遍历序列不唯⼀
算法存在的问题
如果是⾮连通图,则⽆法遍历完所有结点
bool visited[MAX_VERTEX_NUM];
//广度优先遍历
void BFS(Graph G, int v)
{
//从顶点v出发,广度优先遍历图G
visit(v);
//访问初始顶点v
visited[v] = TRUE;
//对v做已访问标记
Enqueue(Q, v);
//顶点v入队列Q
while(!isEmpty(Q))
{
DeQueue(Q, v);
//顶点v出队列
for(w = FirstNeighbor(G, v); w >= 0; w = NextNeighbor(G, v, w)) //检测v所有邻接点
if(!visited[w]) //w为v的尚未访问的邻接顶点visit(w);//访问顶点W
{
visited[w] = TRUE; //对w做已访问标记EnQueue(Q,w); //顶点w入队列
}//if
}//while
}
BFS算法(Final版)
bool visited[MAX_VERTEX_NUM];
void BFSTraverse(Graph G) //对图G进行广度优先遍历for(i=0;i<G.vexnum;++i)visited[i]=FALSE;InitQueue(Q);
{
//访问标记数组初始化//初始化辅助队列Q//从0号顶点开始遍历
for(i = 0; i < G.vexnum; ++i)if(!visited[i])BFS(G, i);
//对每个连通分量调用一次BFS//vi未访问过,从vi开始BFS
}
//广度优先遍历
void BFS(Graph G, int v)
{
//从顶点v出发,广度优先遍历图G
visit(v);
//访问初始顶点v
visited[v] = TRUE;
//对v做已访问标记
Enqueue(Q, v);
//顶点v入队列Q
while(!isEmpty(Q))
{
DeQueue(Q, v);
//顶点v出队列
for(w = FirstNeighbor(G, v); w >= 0; w = NextNeighbor(G, v, w)) //检测v所有邻接点
if(!visited[w]) //w为v的尚未访问的邻接顶点visit(w);//访问顶点w
{
visited[w] = TRUE; //对w做已访问标记EnQueue(Q,w); //顶点w入队列
}//if
}//while
}
复杂度分析
空间复杂度:最坏情况,辅助队列⼤⼩为 O(|V|)
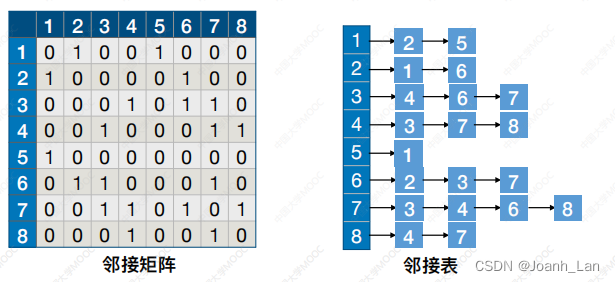
邻接矩阵
\color{red}邻接矩阵
邻接矩阵存储的图:
访问 |V| 个顶点需要O(|V|)的时间
查找每个顶点的邻接点都需要O(|V|)的时间,⽽总共有|V|个顶点
时间复杂度=
O
(
∣
V
∣
2
)
\color{red}O(|V|^2)
O(∣V∣2)
邻接表
\color{red}邻接表
邻接表存储的图:
访问 |V| 个顶点需要O(|V|)的时间
查找各个顶点的邻接点共需要O(|E|)的时间,
时间复杂度=
O
(
∣
V
∣
+
∣
E
∣
)
\color{red}O(|V|+|E|)
O(∣V∣+∣E∣)
⼴度优先生成树

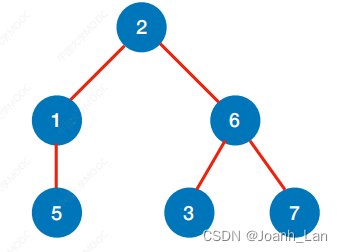
广度优先生成树(Breadth-First Search Tree)是一种图算法,用于以广度优先的方式遍历和生成图的树形结构。该算法从图中的一个起始节点开始,逐层遍历图中的节点,直到遍历完所有与起始节点可达的节点。
广度优先生成树的过程如下:
- 选择一个起始节点作为根节点,并将其标记为已访问。
- 将起始节点入队列。
- 从队列中取出一个节点作为当前节点。
- 遍历当前节点的所有邻接节点:
- 如果邻接节点未被访问过,则将其标记为已访问,并将其加入队列。
- 将当前节点与邻接节点之间的边添加到生成树中。
- 重复步骤3和步骤4,直到队列为空。
广度优先生成树的特点是,它按照节点的层级顺序生成树,即先生成根节点,然后生成与根节点相邻的节点,再生成与这些节点相邻的节点,依次类推。因此,生成的树形结构具有层级感,节点之间的距离相对较近。
广度优先生成树在图算法中有广泛应用,例如最短路径算法、网络分析、社交网络分析等。它能够帮助我们理解和分析图结构,了解节点之间的关系和层级结构。
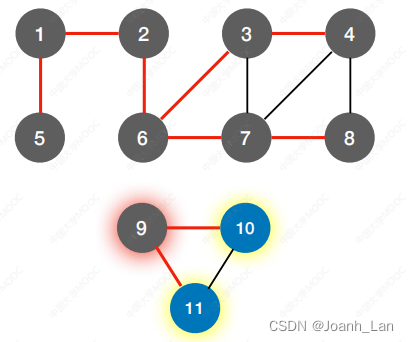
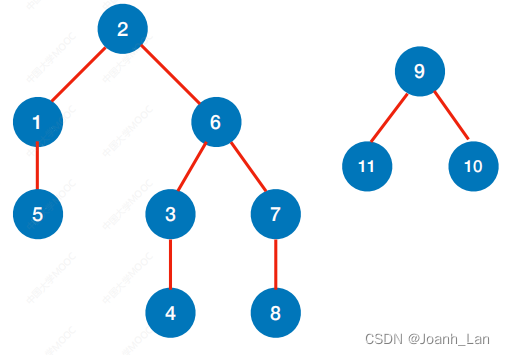
⼴度优先生成森林
广度优先生成森林(Breadth-First Search Forest)是在一个连通图中进行广度优先搜索的结果,其中可能包含多个生成树。每个生成树都是从一个起始节点开始,通过广度优先搜索遍历图中的节点而形成的树状结构。
广度优先生成森林的过程与广度优先生成树类似,只是在遍历图的过程中,如果发现还有未访问的节点,就选择其中一个未访问的节点作为新的起始节点,继续生成一棵新的生成树。这样,通过多次广度优先搜索,可以生成多棵独立的生成树,组成一个森林。
广度优先生成森林的特点是,它可以同时生成多个以不同起始节点为根的生成树,这些生成树之间可能没有直接的连接。每个生成树都是从一个起始节点开始,按照广度优先的方式遍历与其可达的节点,形成一个独立的树形结构。
广度优先生成森林在图算法中也有广泛应用,特别是在处理非连通图时。通过生成森林,我们可以获得图中所有连通分量的结构信息,并且可以对每个连通分量进行进一步的分析和处理。广度优先生成森林可以帮助我们理解和分析图的整体结构,以及不同连通分量之间的关系。
对⾮连通图的⼴度优先遍历,可得到⼴度优先⽣成森林
知识回顾与重要考点