题目
给定一个二叉树,判断它是否是高度平衡的二叉树。
本题中,一棵高度平衡二叉树定义为:
一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。
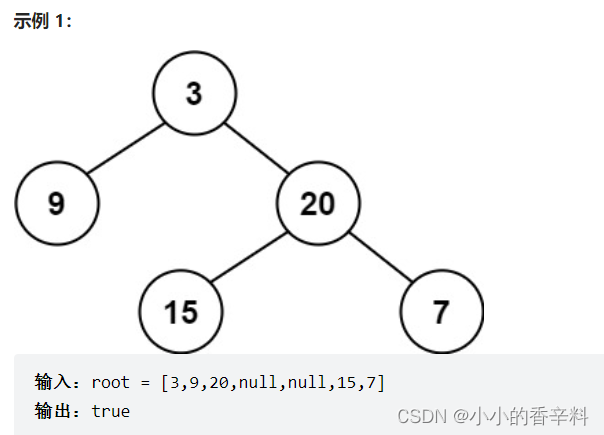
示例 1:
思路
定义一个方法计算给定root的树高度,注意区分二叉树节点的高度和二叉树节点的深度区别!
- 二叉树节点的深度:指从根节点到该节点的最长简单路径边的条数。
- 二叉树节点的高度:指从该节点到叶子节点的最长简单路径边的条数。
接下来写isBalanced方法,使用递归三部曲:
- 确定返回类型:布尔类型,True or False
- 递归出口:如果根为空 或者 根的左右子树都为平衡二叉树且左右子树高度差不超过1,返回True,否则返回False
- 每一层递归逻辑:先调用isBalanced方法递归判断左右子树是否都为平衡二叉树,再求一下左右子树的高度,如果根的左右子树都为平衡二叉树且左右子树高度差不超过1,返回True,否则返回False
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def getHeight(self,root):
if not root:
return 0
return max(self.getHeight(root.left),self.getHeight(root.right))+1
def isBalanced(self, root: Optional[TreeNode]) -> bool:
if not root:
return True
left = self.isBalanced(root.left)
right = self.isBalanced(root.right)
left_h = self.getHeight(root.left)
right_h = self.getHeight(root.right)
if left and right and abs(left_h-right_h)<=1:
return True
else:
return False其实上面的写法并不高效,因为我们如果找到判断完root节点的左右子树是否为平衡二叉树之后,紧接着就去求左右子树的高度,但是如果它的左右子树都不是平衡二叉树,就没必要再求树高了。实际上求树高也占了不少时间,所以直接返回False能高效很多。
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def getHeight(self,root):
if not root:
return 0
return max(self.getHeight(root.left),self.getHeight(root.right))+1
def isBalanced(self, root: Optional[TreeNode]) -> bool:
if not root:
return True
left = self.isBalanced(root.left)
right = self.isBalanced(root.right)
if not left or not right:
return False
left_h = self.getHeight(root.left)
right_h = self.getHeight(root.right)
if abs(left_h-right_h)<=1:
return True
else:
return False看一下时间差距
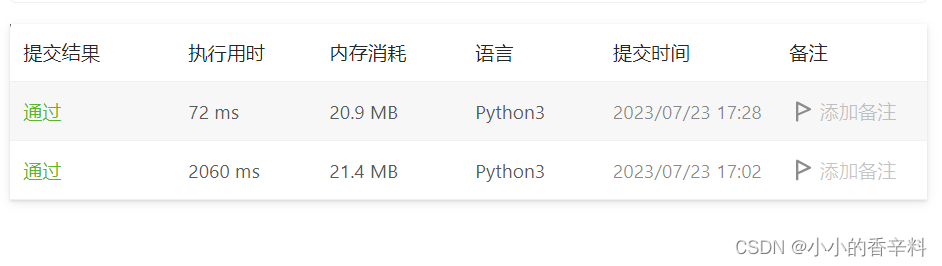
实际上这样效率还是有点低,因为我们是把判断二叉树是否为平衡二叉树的逻辑和树高分开去求了,但是求树高的同时可以顺便判断一下当前数是否为平衡二叉树,这样效率又可以提升。
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def getHeight(self,root):
if not root:
return 0
left = self.getHeight(root.left)
if left==-1:
return -1
right = self.getHeight(root.right)
if right==-1:
return -1
if abs(left-right)>1:
return -1
return -1 if abs(left-right)>1 else max(left,right)+1
def isBalanced(self, root: Optional[TreeNode]) -> bool:
return self.getHeight(root)!=-1