前言

中间呢其实还有两讲，但是那两讲太easy了，根本难不倒你们，所以，我索性不放了~~那我们今天讲一个比较容易的知识点——动态规划（终于没人给我催更了！哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈~~~~~）

咳咳，跑远了，那我们就先开始吧~~

动态规划——递推

动态规划：dynamic programing

以次——状态——计算

档次一下就上来了，对叭~~

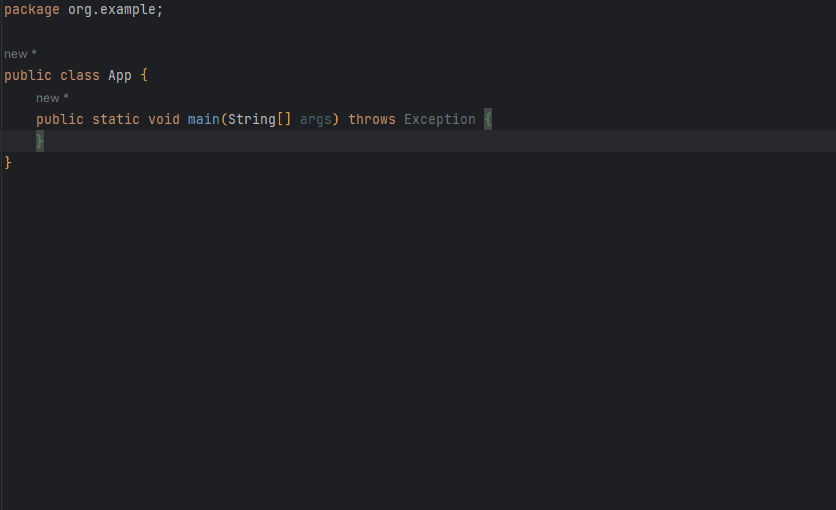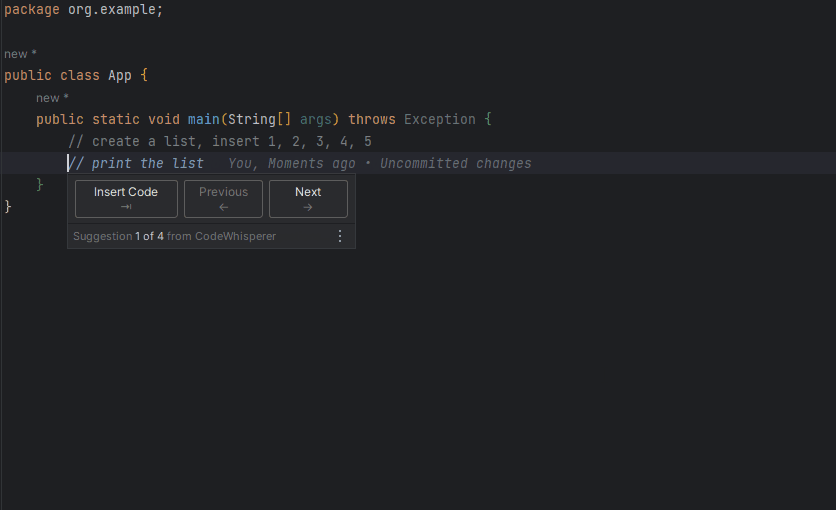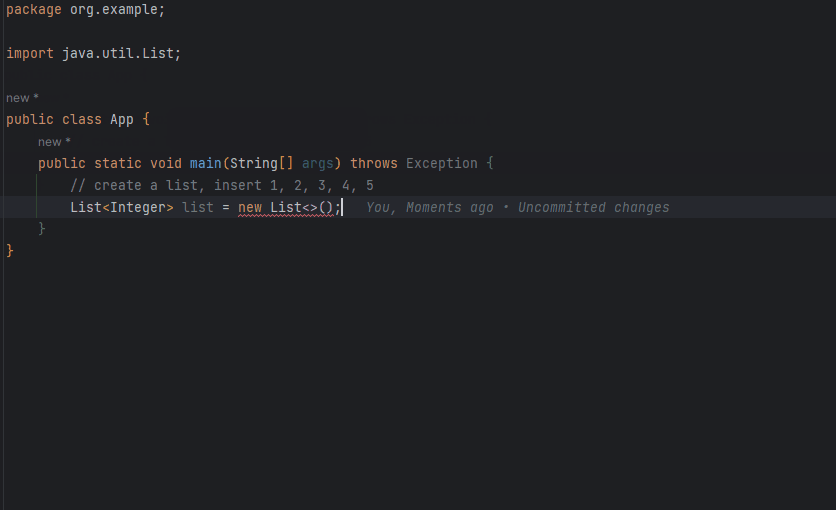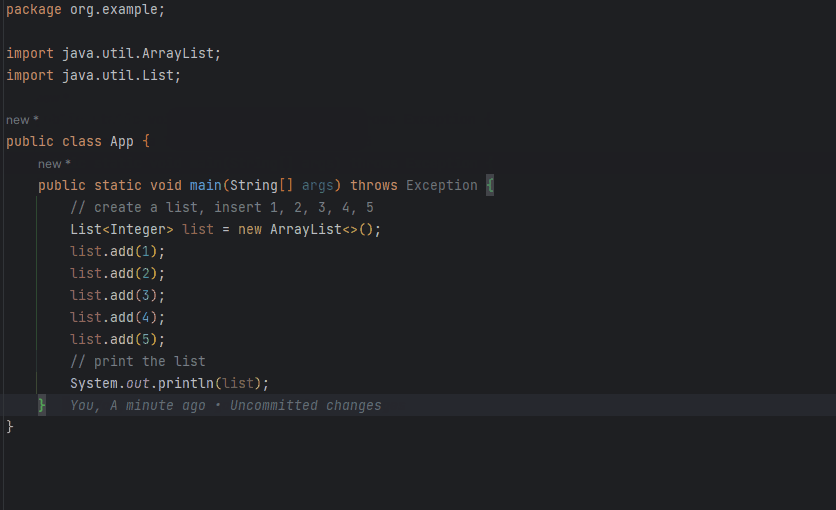
例题——魔鬼步

魔鬼共有n级楼梯要走，魔鬼有他的步伐，每一步他只能向上走a级楼梯或者b级楼梯，请问能否走到底n级？（n<=90）

输入样例就不给了，因为……给了跟没给一样

依次计算

这里我就直接给图了，省点时间

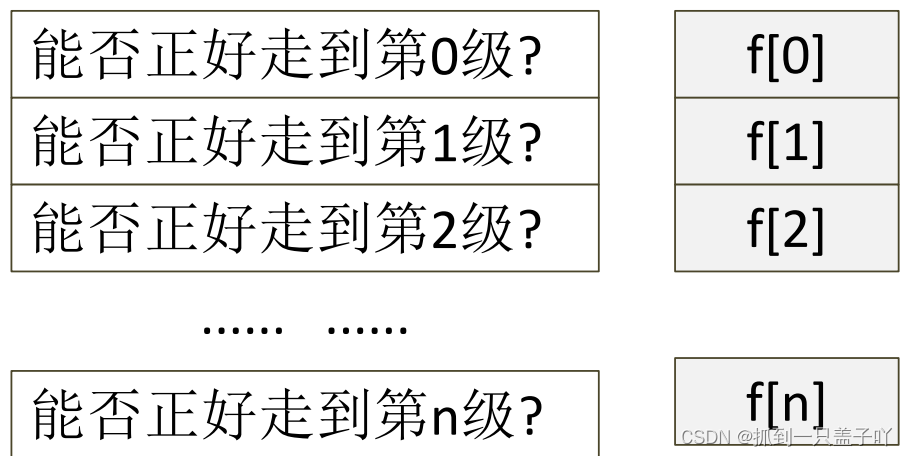
f[i]记录能否正好走到第i级

能否正好走到第i级取决于：
1.能否正好走到第i-a级
2.能否正好走到第i-b级

若i==0:

f[0]=1

若i>=1:

f[i]=f[i-a]|i>=a

或者

f[i-b]|i>=b

定义状态+代码

/*
f[i]记录能否正好走到第i级
输入样例n=10,a=3,b=4
    i=0,1,2,3,4,5,6,7,8,9,10
    f[i]=1,0,0,1,1,0,1,1,1,1,1
*/
#include<iostream>
using namespace std;
bool f[51];
int n,a,b;
int main(){
	cin>>n>>a>>b;
	f[0]=1;
	for(int i=1;i<=n;i++){
		f[i]=0;
		if(i>=a)
		    f[i]=(f[i] or f[i-a]);
		if(i>=b)
		    f[i]=(f[i] or f[i-b]);
	}
	for(int i=0;i<=n;i++)
	    cout<<i<<":"<<f[i]<<endl;
	return 0;
}

f[i]记录能否正好走到第i级
输入样例n=10,a=3,b=4
    i=0,1,2,3,4,5,6,7,8,9,10
    f[i]=1,0,0,1,1,0,1,1,1,1,1

定义状态，手算样例

for(int i=0;i<=n;i++)
	    cout<<i<<":"<<f[i]<<endl;

输出数组，方便调试

例题——魔鬼的步伐

题目描述

魔鬼共有n级楼梯要走，魔鬼有他的步伐，每一步他只可以向上走a级楼梯或者b级楼梯，请问共有多少种不同的走法可以正好走完n级台阶。

输入输出格式

输入格式

输入正整数n，a和b，（n,a,b<=50）,a不等于b。

输出格式

输出一个正整数代表共有多少种走法。

输入输出样例

输入样例:

4 3 5

输出样例:

代码

#include <iostream>
using namespace std;
int main() {
    int n, a, b;
    cin >> n >> a >> b;
    int dp[n+1];
    dp[0] = 1; // 初始状态，到 0 级台阶只有 1 种走法
    for (int i = 1; i <= n; i++) {
        dp[i] = 0;
        if (i >= a) dp[i] += dp[i-a]; // 走 a 级台阶
        if (i >= b) dp[i] += dp[i-b]; // 走 b 级台阶
    }
    cout << dp[n] << endl;
    return 0;
}