目录
1 EXCEL可以用来做假设检验
1.1 如何打开 数据分析 和 规划求解
1.2 EXCEL里关于正态分布的准备知识
2 基本的假设检验
2.1 最基本的假设检验,单边的Z检验
2.1 双样本F检验
2.1.1 例题
2.1.2 进行F检验之前需要满足一些假设条件
2.1.3 计算步骤
2.1.4 如何查表:下面这个图是 显著度a=0.05的F值表
2.1.5 如何分析F检查的结果
2.2
2.5 方差分析(one-way ANOVA)
1 EXCEL可以用来做假设检验
- EXCEL里可以做假设检验的
- 但是需要打开加载项,数据分析才可以

1.1 如何打开 数据分析 和 规划求解
-
开始-----选项-----加载项
-
加载项里选择 数据分析 & 规划求解

1.2 EXCEL里关于正态分布的准备知识
- 正态分布,
- 正态分布曲线图,横轴是x,纵轴是概率p
- 而normsinv是正态分布的反函数,可以根据概率求出 自变量的值
- 函数 normsinv()
- 函数 norm.s.inv()
- 函数 norm.s.dist()
- 作用是在EXCEL里配合使用 normsinv(rand()) 或 normsinv(rand()) 生成一些本身就符合正态分布的数据。
- 如果有其他分布的反函数,理论上也可以生成符合其他分布的数据。



2 基本的假设检验
2.1 最基本的假设检验,单边的Z检验
2.2 双样本F检验
- 最常用的应该就是用来于比较两个或多个组间的平均值是否有显著差异。
- 原假设:一般就是认为符合,没差异等天真假设
- F检验的原假设是所有组之间的差异是出于偶然。换句话说,原假设认为各组之间的平均值没有显著差异。
- F检验的原理是,如果两个或多个组间的平均值或其他统计量之间存在显著差异,则组间方差(inter-group variance)会较大,而组内方差(intra-group variance)较小。
- 因此F值=组间方差 / Σj 组内方差,如果F值越大,证明组间方差>>组内方差
- P值 = 概率(F值 ≥ 实际F值 | 原假设) ,也就是p越小,证明 原假设--相信方差相同/期望相同的概率很小,不是观测造成,而是其他原因造成的。
参考下面的文档
F检验结果应该怎么看? - 知乎F检验是一种统计检验,可用来比较两个或多个组间的平均值是否有显著差异。它是由Ronald Fisher发明的,因…![]() https://www.zhihu.com/question/453744187/answer/2805042211
https://www.zhihu.com/question/453744187/answer/2805042211
2.2.1 例题

2.2.2 进行F检验之前需要满足一些假设条件
- 样本是随机取样的,也就是说,每个组中的观测值是独立的。
- 样本是来自正态分布的总体。
- 每个组的样本容量应该相等
2.2.3 计算步骤
- 需要计算出三组数据的平均值,
- 平均值等于所有数加起来的和除以数据个数。
- 然后计算出组内方差和组间方差。
α (alpha)是显著度
组内方差(intra-group variance)
- 使用样本方差公式,组内方差等于每个数据与其所在组的平均值的差的平方和除以(组内数据个数-1)。
- 因为每种数据的样本容量要相同,i相同
- u1,u2 ... ... 是每组平均数
- 平均数就是最简单得算术平均数,u1=(x1+x2+....+xi)/i
- 如第1组组内方差,δ^2=((u1-x1)^2+(u1-x2)^2+....++(u1-xi)^2)/(i-1)
- 如第2组组内方差,δ^2=((u2-x1)^2+(u2-x2)^2+....++(u2-xi)^2)/(i-1)
组间方差(inter-group variance)
- 使用样本方差公式,组间方差等于每个数据与其所在组的平均值的差的平方和除以(组的数量个数-1)。
- U是多组数据之和=全部数据 的平均值
- 假设有 j 组数组
- 组间方差,δ^2=((U-u1)^2+(U-u2)^2+....++(U-uj)^2)/(j-1)
F值
- F= 组间方差除以组内方差的和。
- F= 组间方差 / Σj 组内方差
- 然后查表,k1组间自由度等于组数减1,k2组内自由度等于每组个数减去组数。
- 下面的例子里,k1=2-1,k2=30-2=28
- 如果F值打羽查表得到的F值,说明差异显著,否则说明差异不显著。
P值的计算公式如下:
- P值 = 概率(F值 ≥ 实际F值 | 原假设)
- 其中,原假设是所有组之间的差异是出于偶然。通过计算,P值可以得到一个概率值,表示在原假设下,观察到如此极端的结果(即F值大于或等于实际观察到的F值)的概率。
- 通常情况下,P值小于0.05被认为是有统计学显著性的,即我们有95%的信心认为样本数据中差异的存在不是偶然造成的,而是由于实验因素或其他因素导致的。
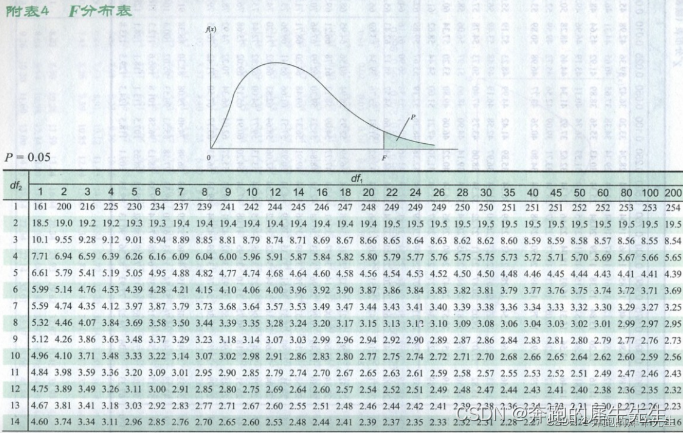
2.2.4 如何查表:下面这个图是 显著度a=0.05的F值表 : F0.05(1,28) =4.2
- k1,组间自由度 =j-1 =2-1 =1
- k2,组内自由度 =i-j =30-2 =28
- 查表得出F值是4.2
- 也就是 F0.05(1,28) =4.2


2.2.5 指标意义
- 在F检验中,p值是指在进行方差分析时,对于给定的数据集,假设所有组之间的差异是出于偶然,计算得到这个假设的的概率。
- 具体来说,p值越小,就说明数据集的差异越显著,越有理由拒绝原假设(即所有组之间的差异是出于偶然),而接受备择假设(即存在显著差异)。换句话说,当p值小于0.05时,我们有95%的信心认为样本数据中差异的存在不是偶然造成的,而是由于实验因素或其他因素导致的。
- 需要注意的是,p值小于0.05只表明差异是显著的存在的,但并不能说明这种差异是否有实际意义或重要性。因此,在进行统计推断时,除了p值外,还需要考虑其他因素,例如效应量的大小和样本大小等,以更全面地评估数据的结果。
- F值表示整个拟合方程的显著性,F越大,表示方程越显著,拟合程度也就越好。
- 另外在统计解释时一般不看F值,只需要看P值就可以了,但是在写论文时还是要将F值写出来,并把P值放在后面用括号括起来
2.2.6 如何分析F检查的结果
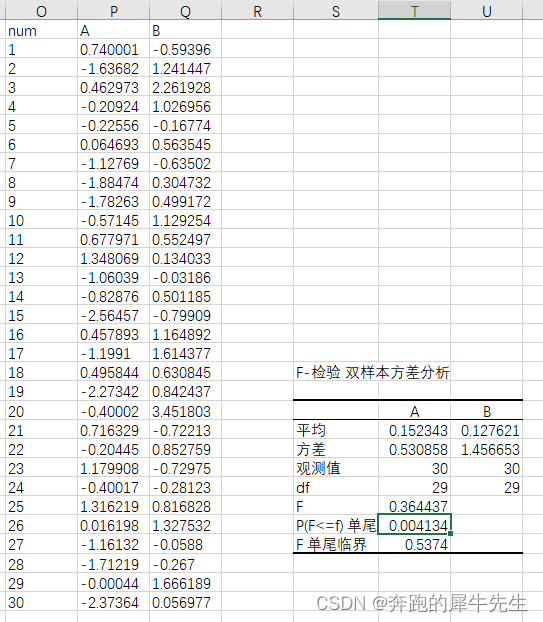
结果如下
- 因为这是F-检验的双样本方差分析
- p=0.48> 0.05 显著度,说明两者方差无明显差异,即方差齐性
- 接着 选用 分析工具 中 的 t 检验 : 双 样本等方差假设

2.3 反向验证结果
因为数据是我用 normsinv() 生造出来的,所以一定是符合正态分布的,所以我打算用这些数据来反向验证F检验的合理性,可靠性。
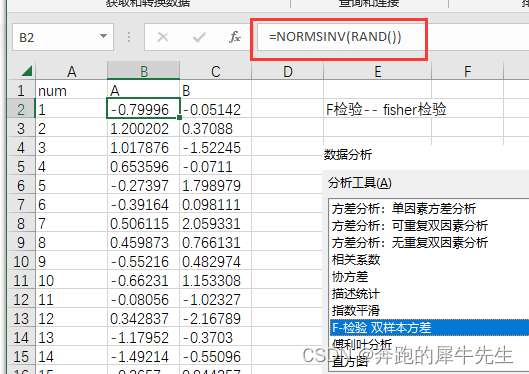

2.3.1 生造2个有偏移量的正态数据
- 两列数据
- 第1列是标准正态数据
- 第2列是标准正态数据+0.5
- p=0.004<0.05 ,说明方差是显著有差异的