题目：

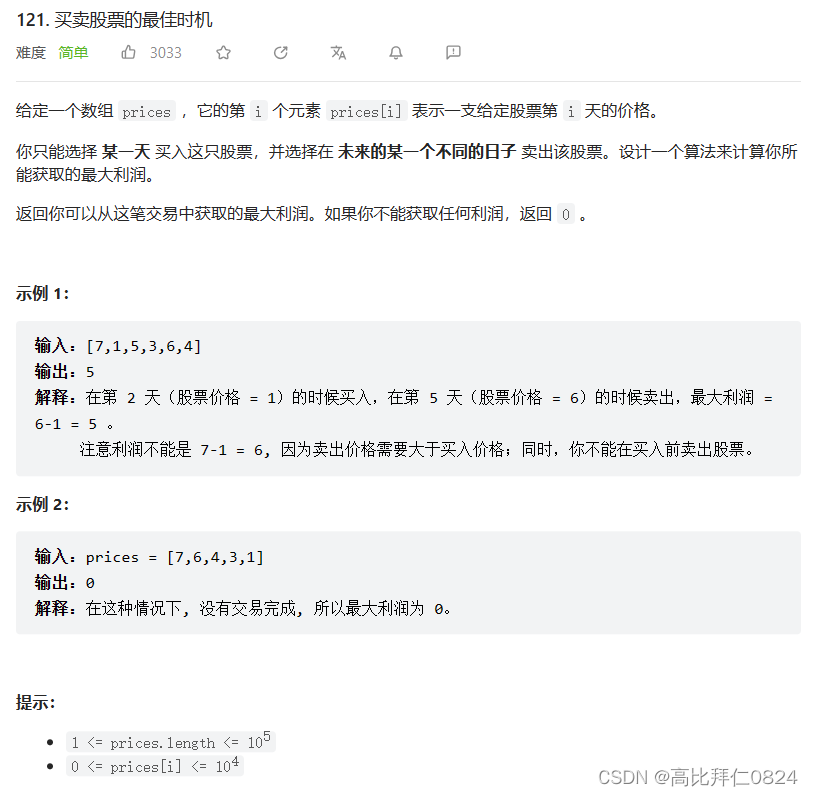
题目链接：121. 买卖股票的最佳时机 - 力扣（LeetCode） 

解题步骤：

下面是用动态规划的思想解决这道题的过程，相信各位小伙伴都能看懂并且掌握这道经典的动规题目滴。说明：以下这种方法并不是最高效的解法，却是最通用的解法，在这一题是最多交易一次，我的解法是针对无论最多交易几次都是通用的，所以下次遇到最多交易多次的题是可以根据这个做法，只要修改一下j的取值范围就可以了，通用性比较强。

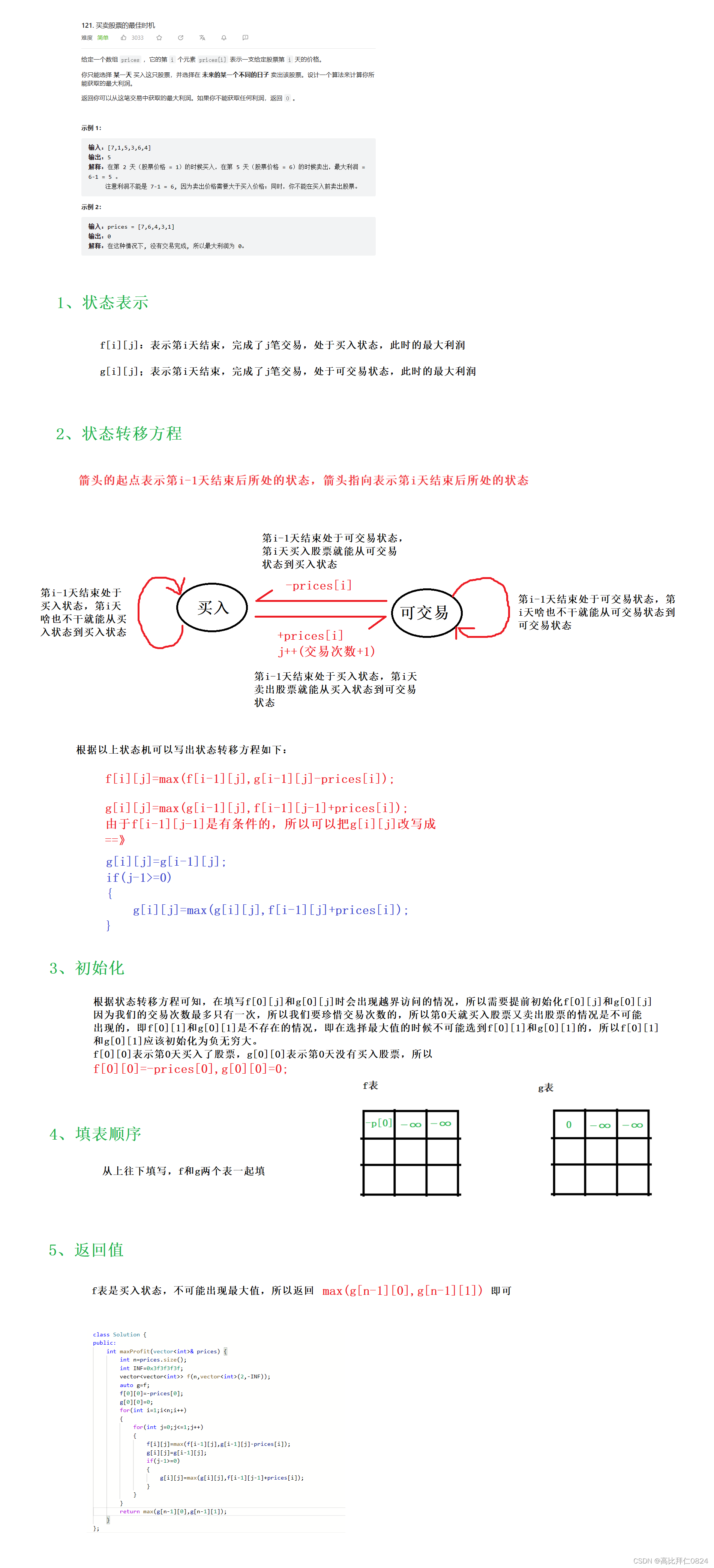
 参考代码：

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int n=prices.size();
        int INF=0x3f3f3f3f;
        vector<vector<int>> f(n,vector<int>(2,-INF));
        auto g=f;
        f[0][0]=-prices[0];
        g[0][0]=0;
        for(int i=1;i<n;i++)
        {
            for(int j=0;j<=1;j++)
            {
                f[i][j]=max(f[i-1][j],g[i-1][j]-prices[i]);
                g[i][j]=g[i-1][j];
                if(j-1>=0)
                {
                    g[i][j]=max(g[i][j],f[i-1][j-1]+prices[i]);
                }
            }
        }
        return max(g[n-1][0],g[n-1][1]);
    }
};

以下这题就是最多进行k次交易的最大利润的题目：

参考代码：

class Solution {
public:
    int maxProfit(int k, vector<int>& prices) {
        const int INF=0x3f3f3f3f;
        int n=prices.size();
        //k可以优化，因为我们有效的交易次数最多是n/2次，不考虑同一天多次买入卖出
        //的无意义的交易，也就是我们就算一天买入，下一天卖出，再下一天买入，再卖出
        //最多也就完成n/2次交易，所以k可以做优化，如果大于n/2就取n/2即可
        k=min(k,n/2);
        vector<vector<int>> f(n,vector<int>(k+1,-INF));
        auto g=f;
        f[0][0]=-prices[0];
        g[0][0]=0;
        for(int i=1;i<n;i++)
        {
            for(int j=0;j<=k;j++)
            {
                f[i][j]=max(f[i-1][j],g[i-1][j]-prices[i]);
                g[i][j]=g[i-1][j];
                if(j-1>=0)
                {
                    g[i][j]=max(g[i][j],f[i-1][j-1]+prices[i]);
                }
            }
        }
        int ret=g[n-1][0];
        for(const auto& e:g[n-1])
        {
            ret=max(ret,e);
        }
        return ret;
    }
};

 

以上就是用动态规划的思想分析这两道题目的整个过程啦，你学会了吗？如果以上题解对你有所帮助，那么就点亮一下小心心，点点关注呗，后期还会持续更新动态规划的经典题目哦，我们下期见啦！！！！！ ！！！！