线性链表简介

线性表的链式存储结构称为线性链表，如图1所示，线性链表将存储空间划分成若干的小块，每块占用若干个字节，这些小块称为存储结点。将其中的存储结点分为两个部分，一部分用于存储数据元素的值，称为数据域；另一部分用于存储元素之间的前后件关系，即存放下一个元素在存储序号（存储地址），指向后件结点。在线性链表中用一个专门的指针 HEAD 指向线性链表中第一个数据元素的结点（即存放第一个元素的地址）。线性表中最后一个元素没有后件，因此，线性链表中的最后一个结点的指针域为空（用 NULL 或0表示），表示链终结。

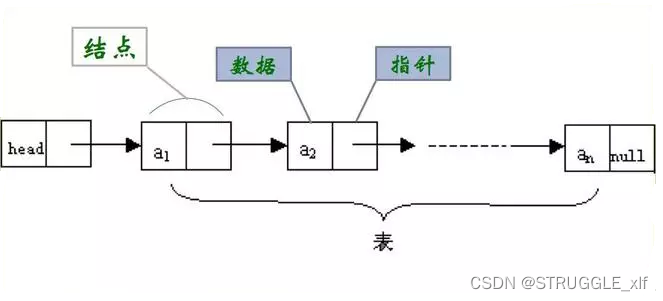
线性链表中各元素的存储序号是不连续的，元素间的前后件关系与位置关系同时也是不一致的，前后件的关系依靠各结点的指针来指示，指向表的第一个元素的指针 HEAD 称为头指针，当HEAD=NULL时，表示该链表为空。对于线性链表，可以从头指针开始，沿着各结点的指针扫描到链表中的所有结点。这种线性链表称为线性单链表，即可以从表头开始向后扫描链表中的所有结点，而不能从中间或表尾结点向前扫描位于该结点之前的元素。

线性链表的实现

1、插入结点

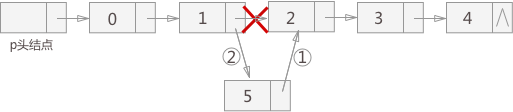
当需要向链表中插入结点时，根据插入位置的不同，可分为3种情形：插入到链表的首部，也就是头结点和首元结点中间；插入到链表中间的某个位置；插入到链表最末端。虽然插入位置有区别，但使用的插入方法是一样的，如图2所示，首先，需要将新结点的 next 指针指向所插入位置后的结点；再插入位置前的结点的 next 指针指向插入结点，即可完成插入操作。

link * insertElem(link * p,int elem,int add){  
    link * temp=p; //创建临时结点temp  
    //首先找到要插入位置的上一个结点  
    for (int i=1; i<add; i++) {  
        if (temp==NULL) {  
            printf("插入位置无效\n");  
            return p;  
        }  
        temp=temp->next;  
    }      
    //创建插入结点c  
    link * c=(link*)malloc(sizeof(link));  
    c->elem=elem;  
    //向链表中插入结点  
    c->next=temp->next;  
    temp->next=c;  
    return  p;  
}  

2、查找与更新

当需要查找线性链表的某个数据时，一般情况下，链表只能通过头结点或者头指针进行访问，所以实现查找某结点最常用的方法就是对链表中的结点进行逐个遍历。代码示例如下：

int selectElem(link * p,int elem){  
    link * t=p;  
    int i=1;  
    while (t->next) {  
        t=t->next;  
        if (t->elem==elem) {  
            return i;  
        }  
        i++;  
    }  
    return -1;  
}  

若需要对链表中的某个结点数据进行修改与更新，首先我们需要通过遍历的方式找到对应的结点，再对其数据域进行更新即可。代码示例如下：

//更新函数，其中，add 表示更改结点在链表中的位置，newElem 为新的数据域的值  
link *amendElem(link * p,int add,int newElem){  
    link * temp=p;  
    temp=temp->next;//在遍历之前，temp指向首元结点  
    //遍历到被删除结点  
    for (int i=1; i<add; i++) {  
        temp=temp->next;  
    }  
    temp->elem=newElem;  
    return p;  
}  

线性表插入功能的实现：

#include<stdio.h>
#include<string.h>
#include<stdlib.h>
struct stu{
    char  name[32];
    struct stu  *next;
};

/*创建链表，参数n是初始化链表时建立的数据个数
prev：指向当前结点的前一个结点
cur：指向当前结点
head：保存表头结点的指针*/
struct stu* CreatList(int n){
    int i;
    char age[12];
    struct stu *prev,*cur,*head;
    head=(struct stu*)malloc(sizeof(struct stu));
    if(head==NULL){
        printf("Can't alloc memory\n");
        return NULL;
    }
    prev=head;
    head->name[0]='\0';
    head->next=NULL;
    for(i=1;i<=n;i++){
        cur=(struct stu*)malloc(sizeof(struct stu));
        if(cur==NULL){
            printf("Can't alloc memory\n");
            return NULL;                
        }
    scanf("%s",cur->name);
    // 请在下面的Begin-End之间补充代码，插入结点。
    /********** Begin *********/
    cur->next = NULL;
    prev->next = cur;
    prev = cur;
    /********** End **********/
    }
    printf("线性链表创建成功！\n");
    return head;
}
/*遍历链表，打印链表数据*/
void Print(struct stu *head){
    struct stu *cur;
    cur=head->next;
    while(cur!=NULL){
        printf("%s\n",cur->name);
        cur=cur->next;
    }
}
int main(){
    int number=3;
    char _name[32];
    struct stu *head,*cur,*fro;
    head=CreatList(number);
    if(head==NULL)
        return -1;
    Print(head);
    return 0;   
}