之前已经介绍过线性回归的基本元素和随机梯度下降法及优化，现在把线性回归讲解完：

矢量化加速

在训练模型时，我们常希望能够同时处理小批量样本，所以我们需要对计算进行矢量化，从而利用线性代数库，而不是使用效率低下的for循环，下面通过代码来直观展示矢量化的高效：

import math
import time
import numpy as np
import torch
from d2l import torch as d2l

n = 10000
a = torch.ones([n])
b = torch.ones([n])

# 定义一个计时器
# 注释#@save是一个特殊的标记，会将对应的函数、类或语句保存在d2l包中
class Timer:  #@save
    """记录多次运行时间"""
    def __init__(self):
        self.times = []
        self.start()

    def start(self):
        """启动计时器"""
        self.tik = time.time()

    def stop(self):
        """停止计时器并将时间记录在列表中"""
        self.times.append(time.time() - self.tik)
        return self.times[-1]

    def avg(self):
        """返回平均时间"""
        return sum(self.times) / len(self.times)

    def sum(self):
        """返回时间和"""
        return sum(self.times)

    def cumsum(self):
        """返回累计时间"""
        return np.array(self.times).cumsum().tolist()

# 计算for循环时间
c = torch.zeros(n)
timer = Timer()
for i in range(n):
    c[i] = a[i] + b[i]
print(f'for循环所用时间：{timer.stop():.9f} sec')

# 计算重载的+运算符来计算按元素的和
timer.start()
d = a + b
print(f'矢量化加速所用时间：{timer.stop():.9f} sec')

结果：

for循环所用时间：0.133013725 sec
矢量化加速所用时间：0.001002550 sec

正态分布与平方损失

在这里，通过对噪声分布的假设来解读平方损失目标函数。
正态分布（高斯分布）与线性回归的关系很密切。
概率分布概率密度函数如下：
$$p(x)=\frac{1}{\sqrt{2\pi {\sigma }^2}}exp(-\frac{1}{2{\sigma }^2}(x-\mu {)}^2)$$
接下来对正态分布进行可视化，代码如下：

import math
import numpy as np
import torch
from d2l import torch as d2l
import matplotlib.pyplot as plt

# 定义正态分布函数
def normal(x, mu, sigma):
    p = 1 / math.sqrt(2 * math.pi * sigma**2)
    return p * np.exp(-0.5 / sigma**2 * (x - mu)**2)

# 可视化正态分布

# 使用numpy进行可视化
x = np.arange(-7, 7, 0.01)
# 均值和标准差对
params = [(0, 1), (0, 2), (3, 1)]
d2l.plot(x, [normal(x, mu, sigma) for mu, sigma in params], xlabel='x',
         ylabel='p(x)', figsize=(4.5, 2.5),
         legend=[f'mean {mu}, std{sigma}' for mu, sigma in params])
d2l.plt.show()

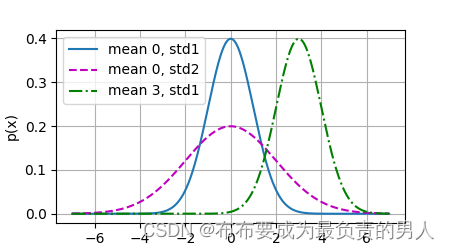
可以发现，改变均值会产生沿x轴的偏移，增加方差会分散分布、降低峰值。
下面内容学之前先复习一下极大似然估计，很多地方都自己推一下印象很深刻
均方误差损失函数（简称均方损失）可以用于线性回归的原因是：我们假设了观测中包含噪声，其中噪声服从正态分布。噪声正态分布如下式：
$$\begin{gathered} y=w^{T}x+b+\delta \\ 其中，\delta 符合正态分布N(0,{\sigma }^2) \end{gathered}$$
因此，我们可以写出通过给定的x观测到特定y的似然：
$$P(y|x)=\frac{1}{\sqrt{2\pi {\sigma }^2}}exp(-\frac{1}{2{\sigma }^2}(y-w^{T}x-b{)}^2)$$
现在，根据极大似然估计法，参数w和b的最优值是使整个数据集的似然最大的值：
$$P(y|X)=\prod _{i=1}^{n}p(y^{(i)}|x^{(i)})$$
根据极大似然估计法选择的估计量称为极大似然估计量。虽然会让很多指数函数的乘积最大化看起来很困难，但是可以在不改变目标情况下，通过最大化似然对数来简化，最终得到式子：
$$-logP(y|X)=\sum _{i=1}^n\frac{1}{2}log(2\pi {\sigma }^2)+\frac{1}{2{\sigma }^2}(y^{(i)}-w^T{x}^{(i)}-b{)}^2$$
现在只需要假设σ是某个固定常数就可以忽略第一项，因为第一项不依赖于w和b。第二项除了常数外，其余部分和前面介绍的均方误差是一样的。
上式的解不依赖于σ，因此，在高斯噪声的假设下，最小化均方误差等价于对线性模型的极大似然估计。

从线性回归到深度网络

神经网络图

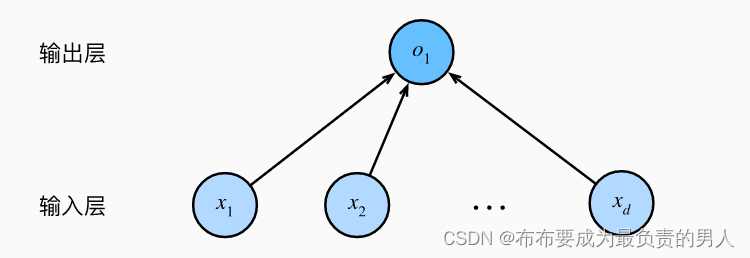
如上图，就是讲线性回归模型描述为了神经网络，容易看出它是单层神经网络，该图只展示了连接模式，略去了权重和偏置。
该图中的特征维度（输入层中的输入数）为d。
对于线性回归，每个输入都与输出相连，成这种变换为全连接层

生物学

树突接收来自其他神经元的信息xi，该信息通过突触权重wi来加权，来确定输入的影响（通过xi与wi相乘来激活或抑制）。
来自多个源的加权输入以加权和
$$y=\sum x_i{w}_i+b$$
的形式汇聚在细胞核中，将这些信息发送到轴突y中进一步处理，通常会通过σ(y)进行一些非线性处理。之后要么到达目的地（如肌肉）要么进入另一个神经元。