1.最小栈

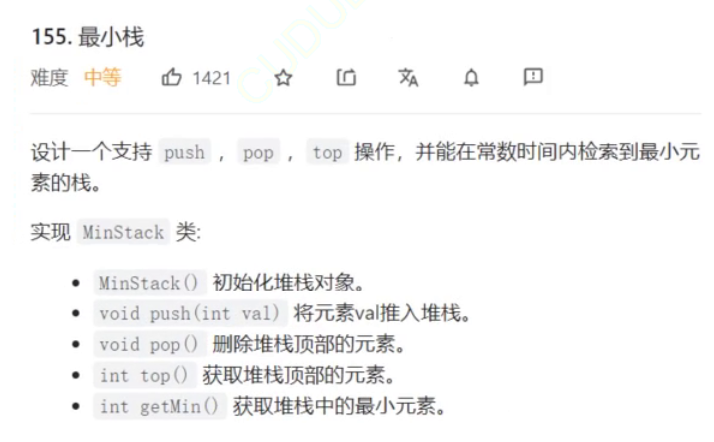
class MinStack
{
public:
	MinStack()
	{

	}
	void push(int val)
	{
		_st.push(val);
		//empty放在前面 因为栈为空时top会assert
		if (_mst.empty() || val <= _mst.top())
			_mst.push(val);
	}
    //注意代码顺序
	void pop()
	{
		if (_mst.top() == _st.top())
			_mst.pop();
		_st.pop();
	}
	int top()
	{
		return _st.top();
	}
	int getMin()
	{
		return  _mst.top();
	}
private:
	stack<int> _st;
	stack<int> _mst;
};

2.栈的压入、弹出序列

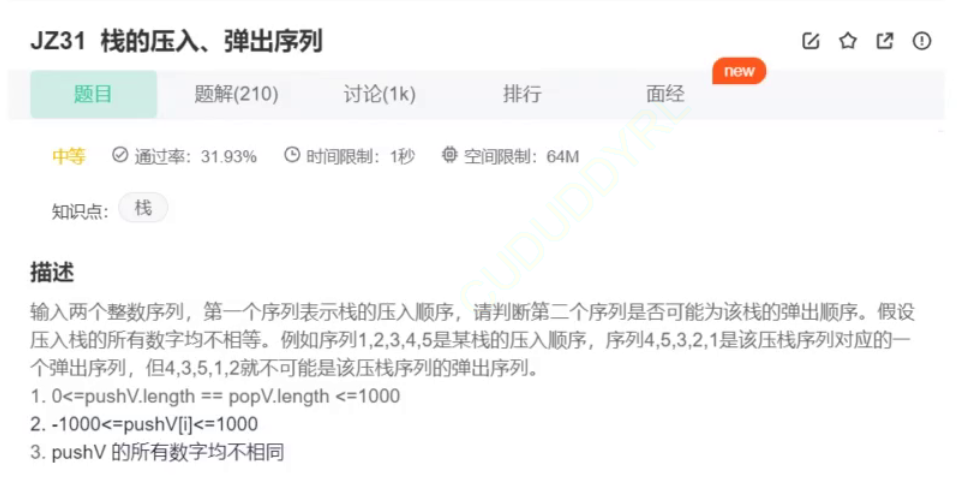
class Solution
{
	//pushV：压栈顺序组
	// popV：出栈顺序组
	bool IsPopOrder(vector<int> pushV, vector<int> popV)
	{
		stack<int> st;
		int i = 0;
		//遍历压栈组
		for (auto x : pushV)
		{
			st.push(x);
			//top前一定判空
			while (!st.empty() && popV[i] == st.top())
			{
				//st非空前提下 判断出栈组与栈顶是否相同
				//相同i后移 -- 可视为出栈正确 -- 继续遍历
				++i;
				//将符合的栈顶数据弹出
				st.pop();

				//继续循环 -- 压栈到中途 -- 连续出栈 
				//此时就会有多组匹配
			}
		}
		//若出栈顺序正确 -- 此时下标i与size大小同
		//return i == popV.size();
		return st.empty();
	}
};

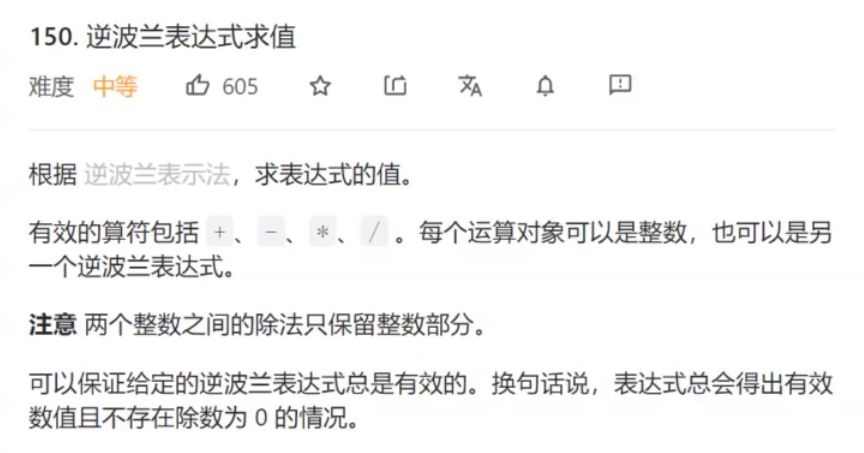
3.逆波兰表达式（后缀表达式）求值

3.1后缀表达式求值

class Solution 
{
public:
	//Evaluate inverse Polish notation
	int evalRPN(vector<string>& tokens)
	{
		stack<long long> st;
		for (auto& str : tokens)
		{
			if (str == "+" || str == "-" 
			 || str == "*" || str == "/" )
			{
				long long right = st.top();
				st.pop();
				long long left = st.top();
				st.pop();
				switch (str[0])
				{
				case '+':
					st.push(left + right);
					break;
				case '-':
					st.push(left - right);
					break;
				case '*':
					st.push(left * right);
					break;
				case '/':
					st.push(left / right);
					break;
				}
			}
			else
			{
				st.push(stoll(str));
			}
		}
		return st.top();
	}
};

3.2中缀表达式转后缀表达式

1.操作数输出
2.操作符：
2.1栈为空或此操作符比栈顶操作符优先级高：压栈
2.2此操作符比栈顶操作符优先级低或相等：输出并pop

3.3带有括号的中缀表达式转后缀表达式

1.操作数输出
2.操作符：
2.1栈为空或此操作符比栈顶操作符优先级高：压栈
2.2此操作符比栈顶操作符优先级低或相等：输出并pop
2.3若遇到左括号：此后的第一个操作符默认运算级最高