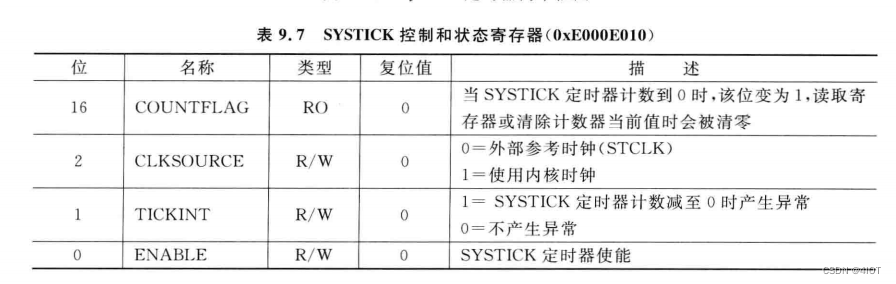
一、Xmind整理:
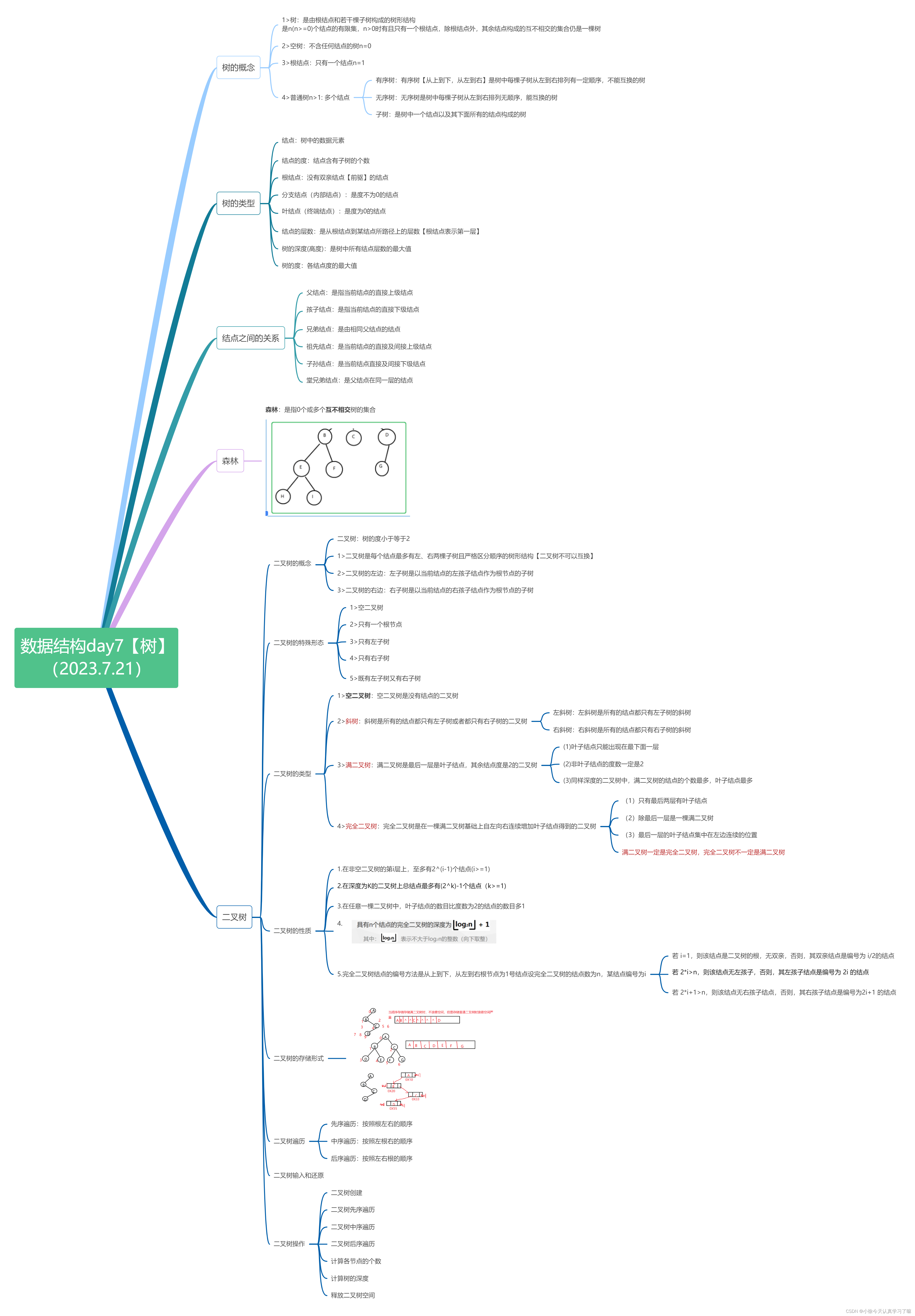
二、课上练习:
练习1:结点之间的关系
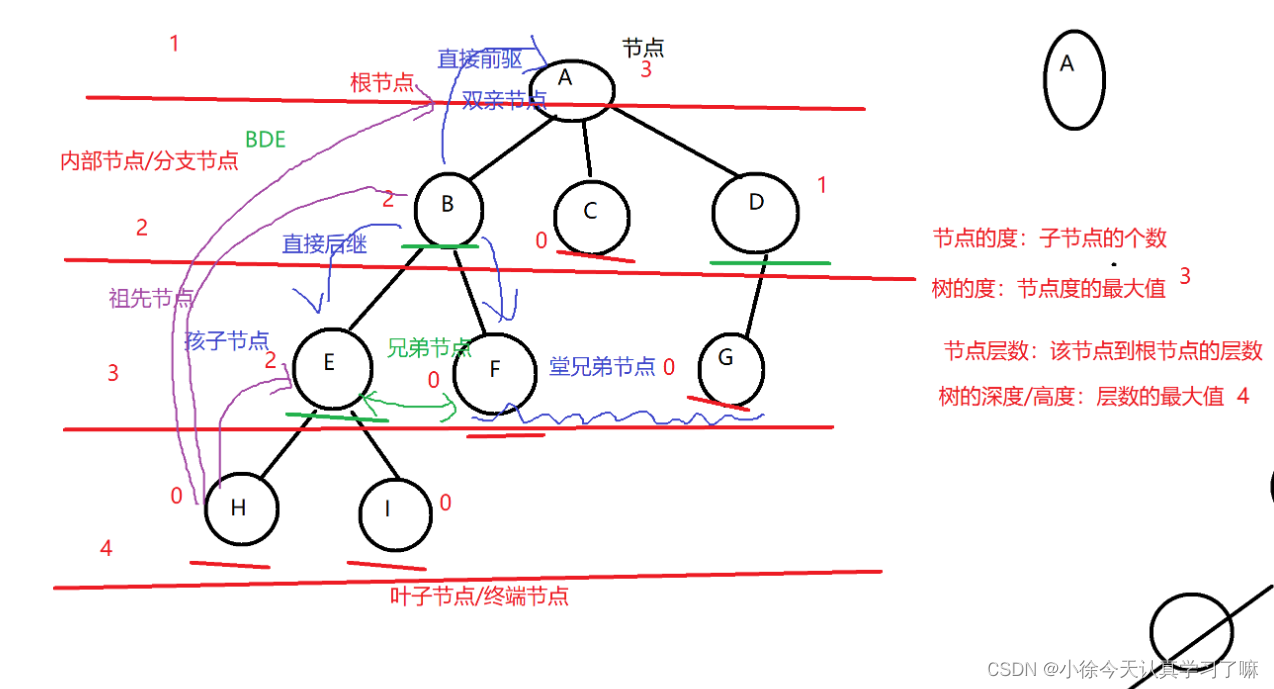
练习2:二叉树的特殊形态
练习3:满二叉树的形态
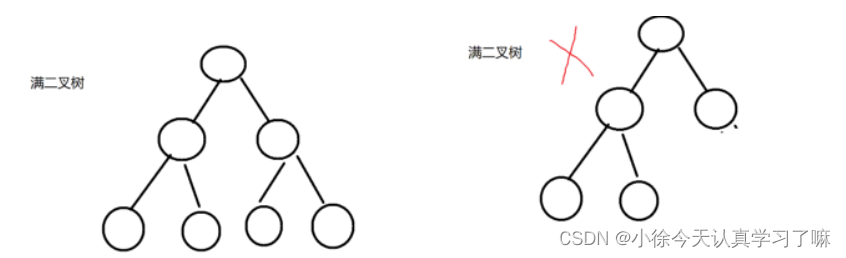
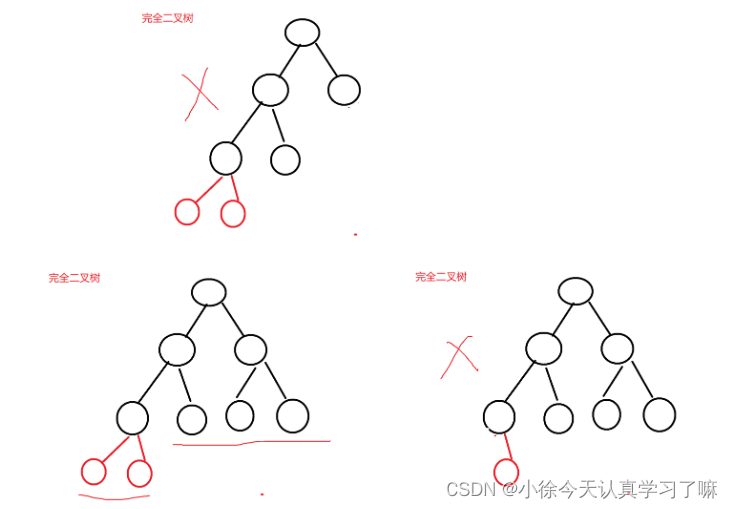
练习4:完全二叉树的形态
满二叉树一定是完全二叉树,完全二叉树不一定是满二叉树
练习5:二叉树的性质与结点的计算
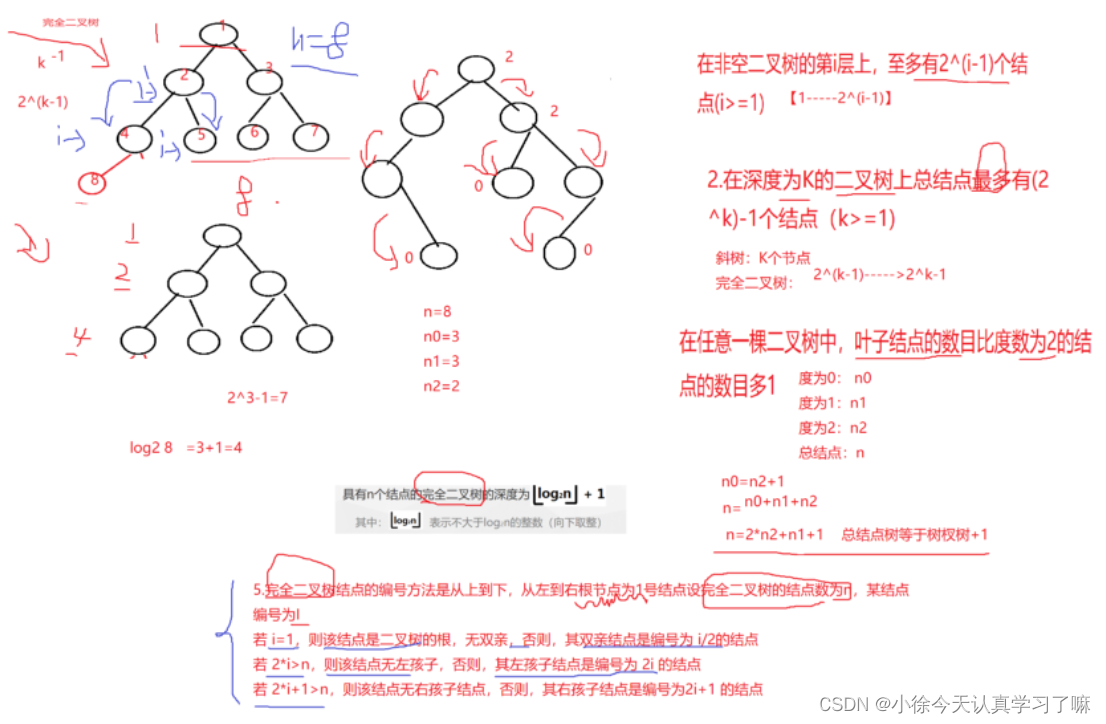
练习6:在一棵度为3的树中,度为3的结点数为2个,度为2的结点数为1个,度为1的结点数为2个,则度为0的结点数不可能为(BCD)个
A、6 B、7 C、4 D、5
答:根据公式可得:n=3*n3+2*n2+1*n1+1=3*2+2*1+1*2+1=11
n=n0+n1+n2+n3 --> n0=n-n1-n2-n3
=11-2-1-2
=6
已求得度为0的结点数为6个,所以不可能的便是BCD。
练习7:设树T的度为4,其中度为1,2,3和4的结点个数分别为4,2,2,1,则T中的叶子数不可能是(ABC)
A、5 B、8 C、6 D、10
答:根据公式可得:n=4*n4+3*n3+2*n2+1*n1+1=4*1+3*2+2*2+1*4+1=19
n=n0+n1+n2+n3+n4 --> n0=n-n1-n2-n3-n4
=19-4-2-2-1 =10
已求得度为0的结点数为10个(即叶子数为10),所以不可能的便是ABC。
练习8:深度为5的完全二叉树最少有多少个结点(C)
A、32 B、16 C、31 D、15
答:对于深度为k的完全二叉树,最少的结点数为2^k - 1。因此,深度为5的完全二叉树最少有2^5 - 1 = 31个结点。所以,深度为5的完全二叉树最少有31个结点。
练习9:已知一棵完全二叉树有500个结点,则这棵树的深度是(D)
A、7 B、8 C、10 D、9
答:如果一棵完全二叉树具有500个结点,我们需要找到这棵树的深度。在一个完全二叉树中,有n个结点的深度可以通过以下公式计算:
对于这个问题,我们有500个节点,所以计算深度的公式为:
k = log2(500) ≈ log2(500) ≈ 8-9(8以上,不到9)
由于深度必须是整数,我们向下取整得到深度为8,再对8+1=9
因此,这棵树的深度为9。
练习10:若有一棵有16个结点的完全二叉树按层编号,则对于编号为7的结点X,它的双亲结点及右孩子结点的编号分别为(B)
A、2,15 B、3,15 C、2,14 D、3,14
答:在一棵按层编号的完全二叉树中,对于编号为X的结点,其双亲结点的编号为X/2,右孩子结点的编号为2X+1。对于编号为7的结点X,可以根据上述规则计算:
双亲结点的编号:7/2 = 3.5,由于结点编号为整数,所以取下整,即双亲结点的编号为3。
右孩子结点的编号:2 * 7 + 1 = 15。
因此,编号为7的结点X的双亲结点的编号为3,右孩子结点的编号为15。
练习11:一个具有63个结点的二叉树的高H的值可能是(ABD)
A、63 B、10 C、5 D、6
答:如果一棵二叉树具有63个结点,我们需要找到这棵树的深度。在一个完全二叉树中,有n个结点的深度可以通过以下公式计算:
对于这个问题,我们有63个节点,所以计算深度的公式为:
k = log2(63) ≈ log2(63) ≈ 5-6(5以上,不到6)
由于深度必须是整数,我们向下取整得到深度为5,再对5+1=6
因此,具有63个结点的二叉树的高度H的可能值在6到63之间。
综上所述,具有63个结点的二叉树的高度H的值可以是6到63之间的任何整数值。
练习12:已知一棵完全二叉树有5层,则第5层最少和最多分别有(A)个结点
A、1,16 B、2,15 C、1,31 D、1,17
答:在一棵完全二叉树中,k层的结点个数最少为2^(k-1),最多为2^k-1。
根据题目给出的信息,完全二叉树有5层。
5层的结点个数最少为2^(5-1) = 2^4 = 16个。
5层的结点个数最多为2^5-1 = 2^5 - 1 = 31个。
前四层的结点个数为:2^4-1=15个
所以第5层最少:16-15=1 最多:31-15=16
因此,第5层最少有1个节点,最多有16个节点。
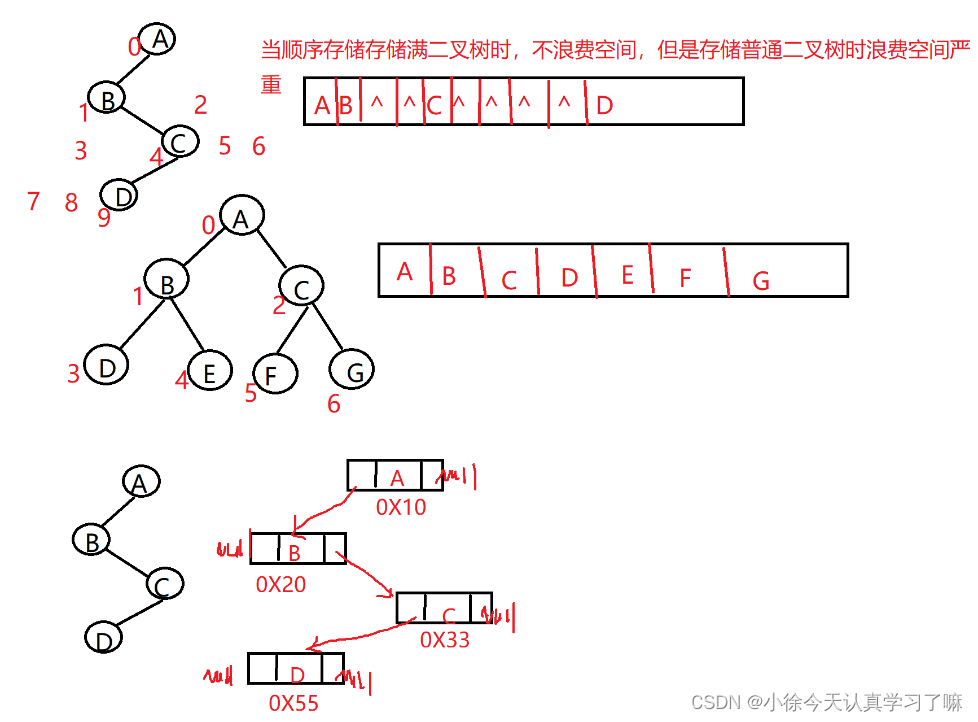
练习13:二叉树的存储形式
练习14:已知遍历结果如下,试画出对应的二叉树
前序:A B C E H F I J D G K
中序:A H E C I F J B D K G
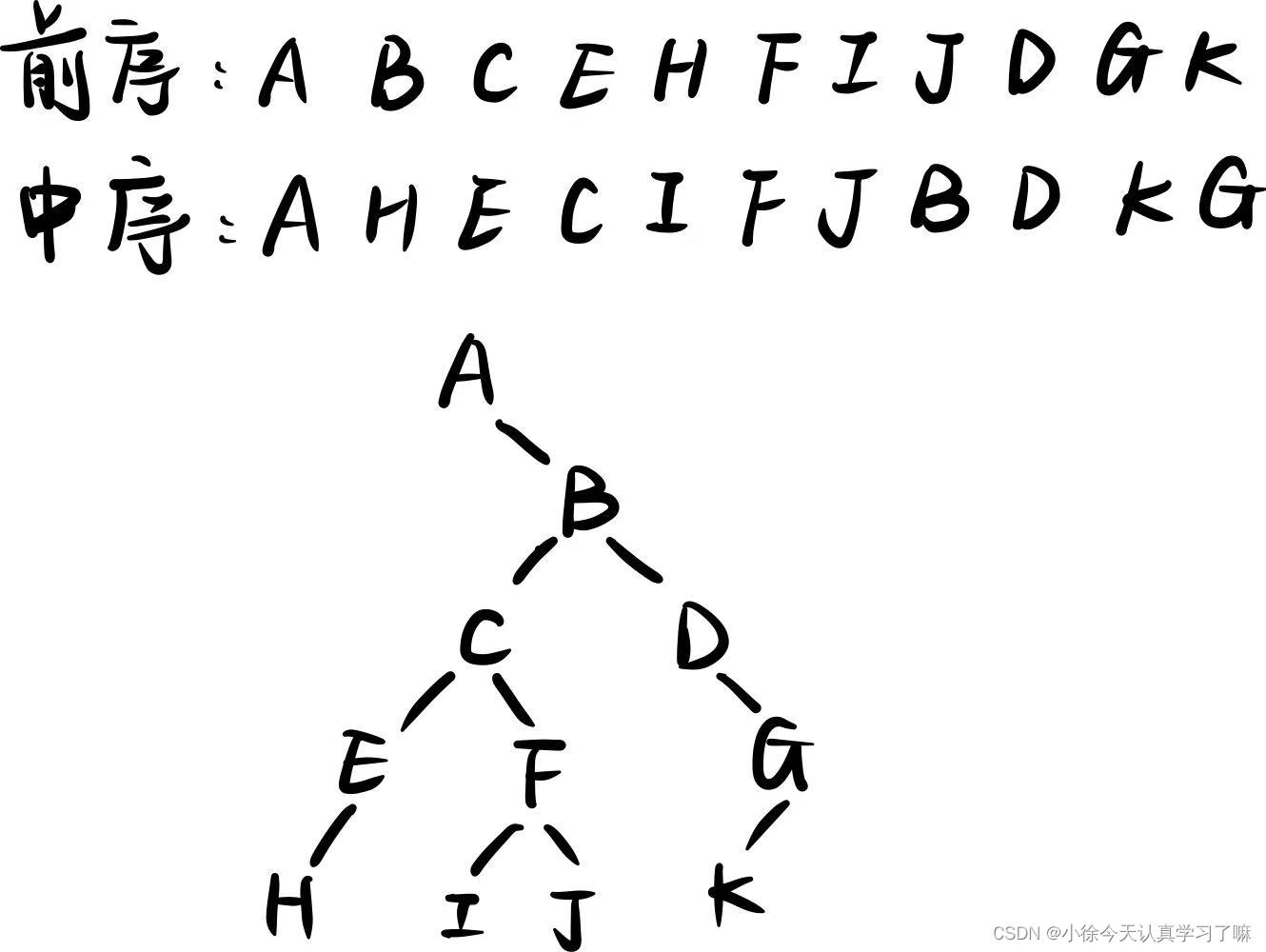
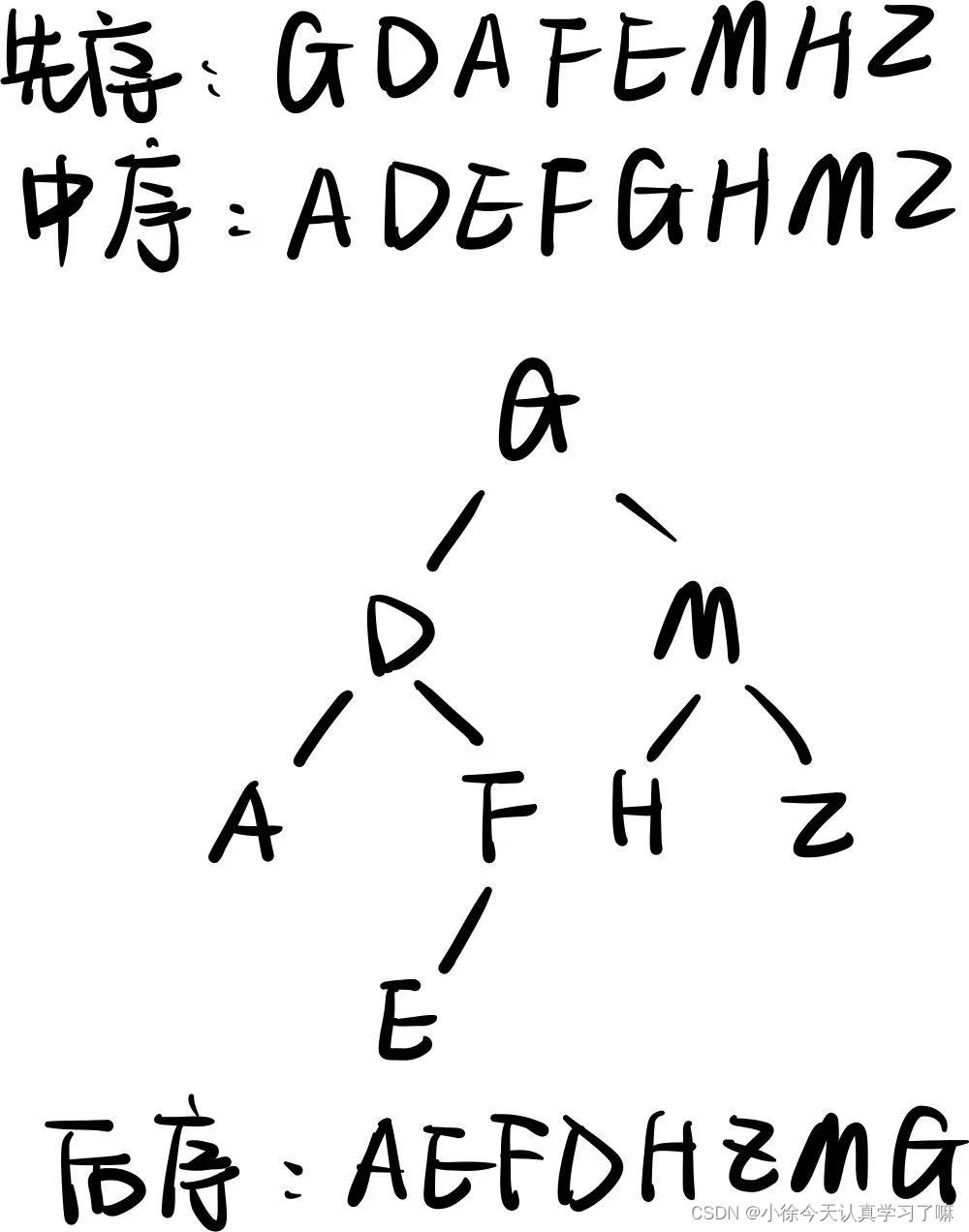
练习15:已知树的先序遍历是GDAFEMHZ,中序遍历是ADEFGHMZ,则后序遍历的结果是(C)
A、AEFDMZHG B、ADFEHZMG C、AEFDHZMG D、AMZHEFDG
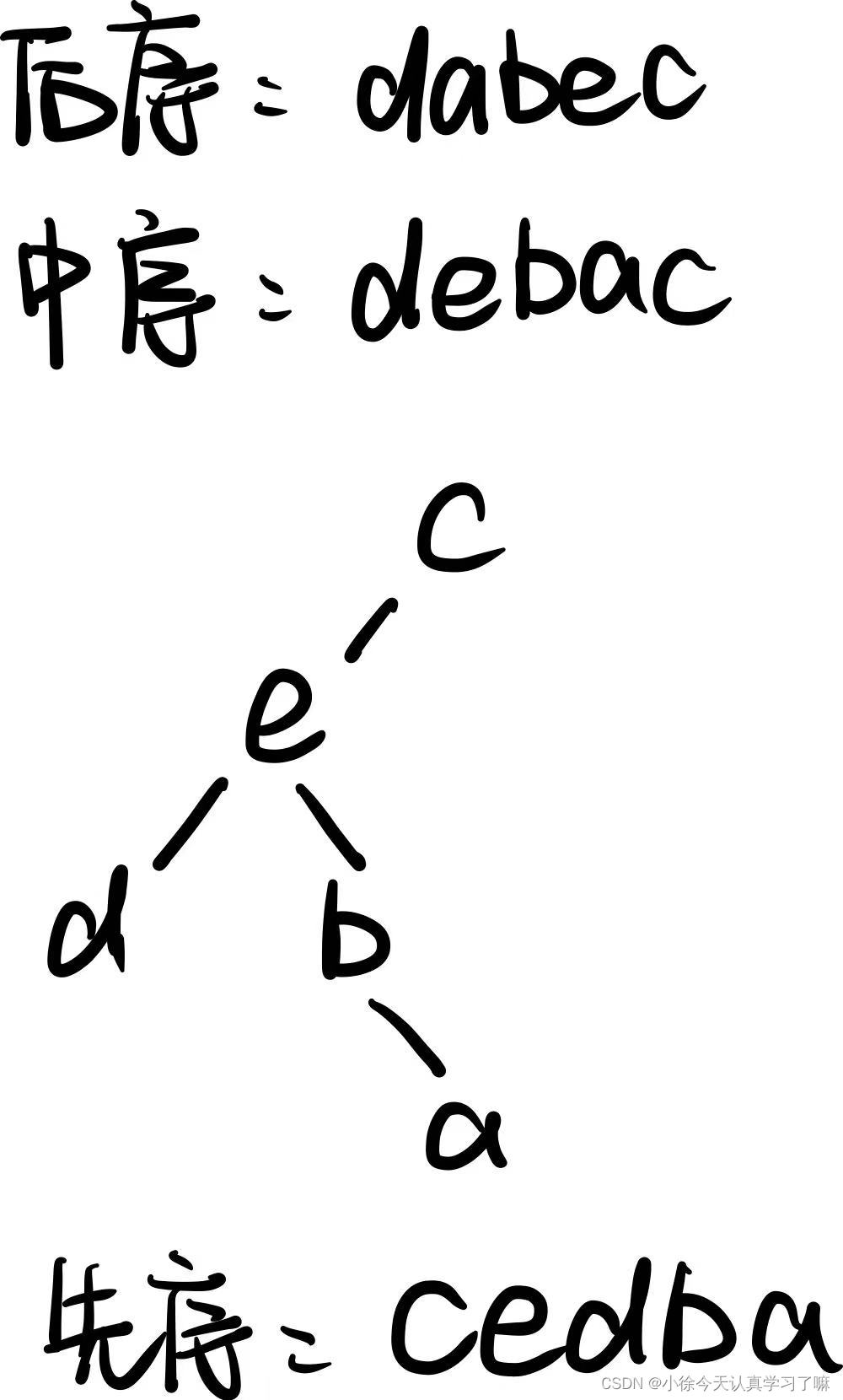
练习16:已知某二叉树的后序遍历序列是dabec,中序遍历序列是debac,它的先序遍历是(B)
A、acbed B、cedba C、decab D、deabc
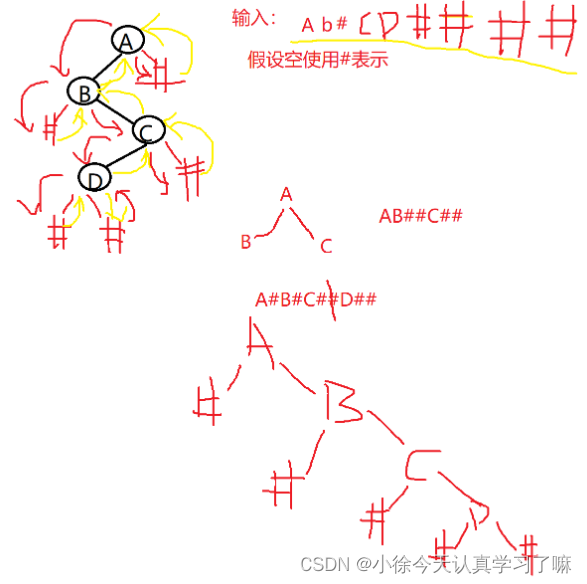
练习17:二叉树输入和还原
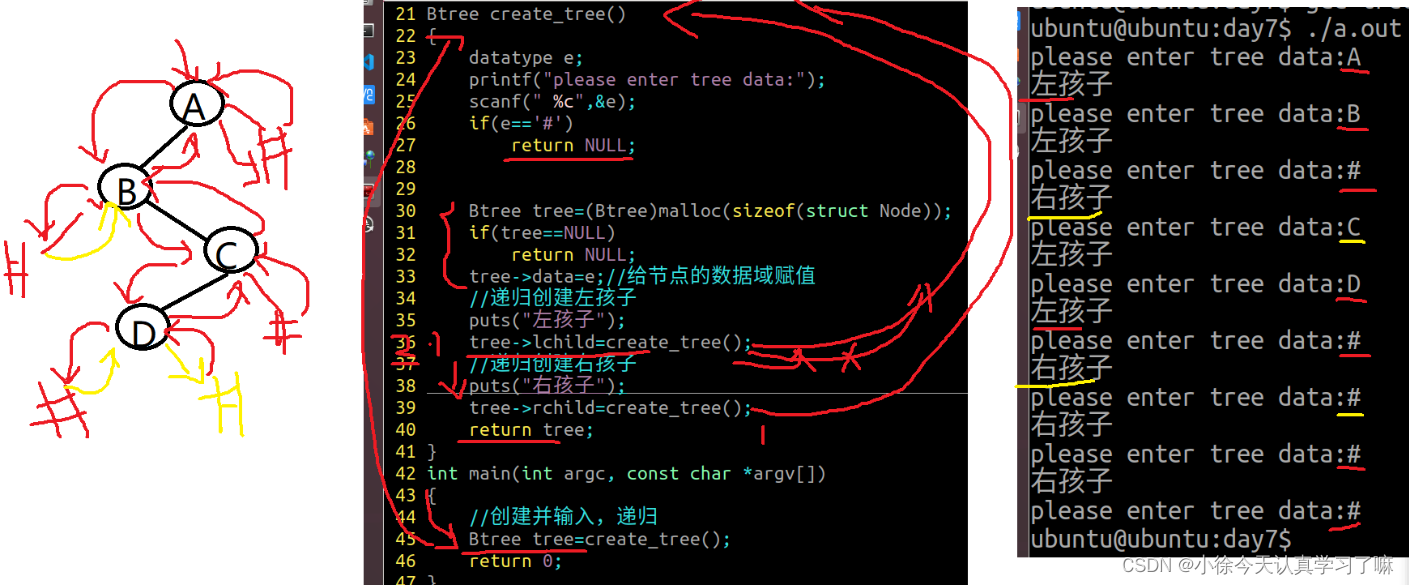
练习18:二叉树创建
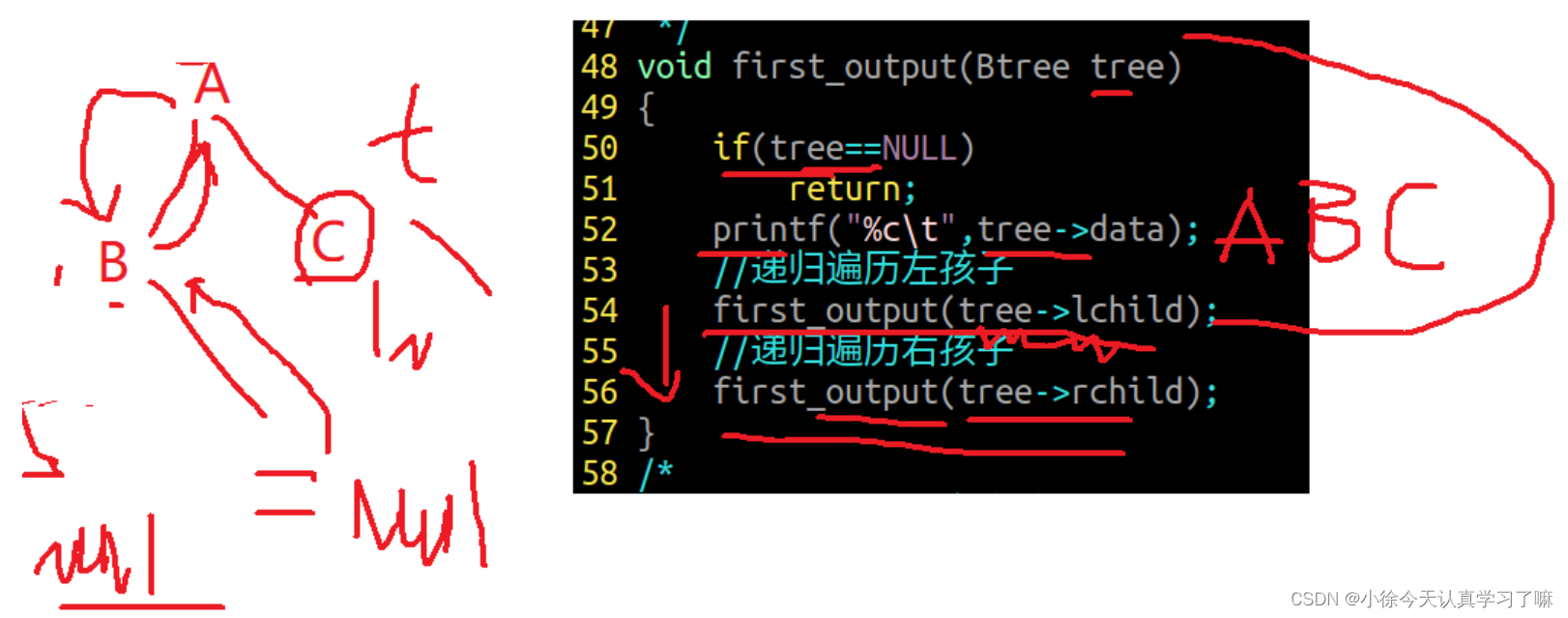
练习19:二叉树先序遍历
练习20:二叉树中序遍历

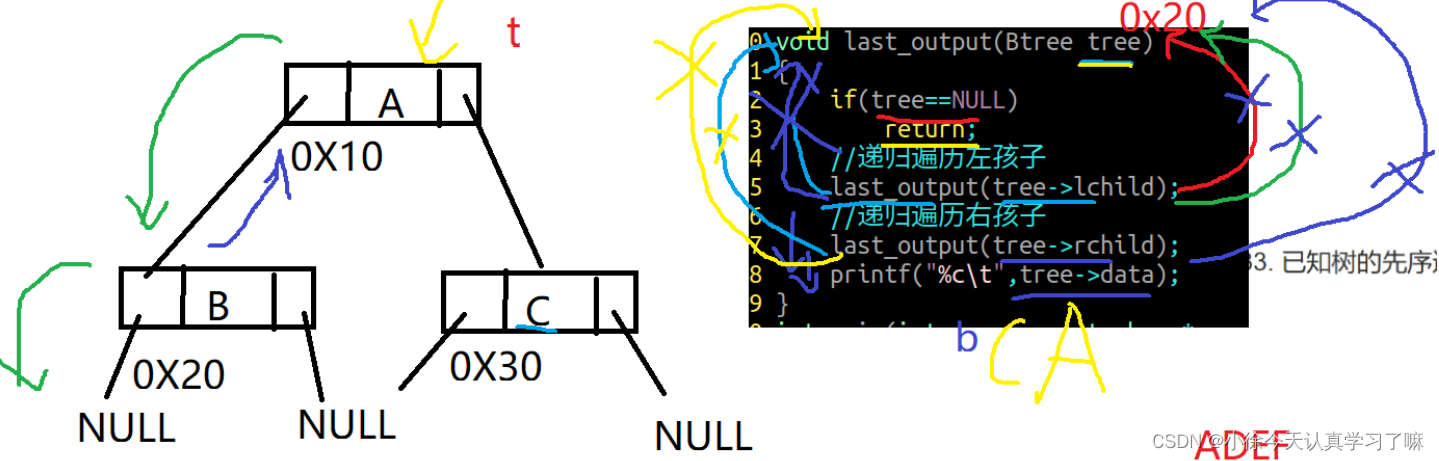
练习21:二叉树后序遍历
练习22:计算各节点的个数
void Count(Btree tree,int *n0,int *n1,int *n2)
{
if(tree==NULL)
return;
if(tree->lchild==NULL && tree->rchild==NULL)
(*n0)++;//++*n0
else if(tree->lchild!=NULL && tree->rchild!=NULL)
(*n2)++;
else
(*n1)++;
Count(tree->lchild,n0,n1,n2);
Count(tree->rchild,n0,n1,n2);
}练习23:计算树的深度
int High(Btree tree)
{
if(tree==NULL)
return 0;
int left=High(tree->lchild)+1;
int right=High(tree->rchild)+1;
return left>right?left:right;
}
练习24:释放二叉树空间
void free_space(Btree tree)
{
if(tree==NULL)
return ;
free_space(tree->lchild);
free_space(tree->rchild);
free(tree);
tree=NULL;
}二叉树的整体代码:
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
typedef char datatype;
typedef struct Node
{
//数据域
datatype data;
//左孩子
struct Node *lchild;
//右孩子
struct Node *rchild;
}*Btree;
/*
* function: 创建二叉树
* @param [ in]
* @param [out]
* @return 返回二叉树的根节点地址
*/
Btree create_tree()
{
datatype e;
printf("please enter tree data:");
scanf(" %c",&e);
if(e=='#')
return NULL;
Btree tree=(Btree)malloc(sizeof(struct Node));
if(tree==NULL)
return NULL;
tree->data=e;//给节点的数据域赋值
//递归创建左孩子
puts("左孩子");
tree->lchild=create_tree();
//递归创建右孩子
puts("右孩子");
tree->rchild=create_tree();
return tree;
}
/*
* function: 先序遍历
* @param [ in]
* @param [out]
* @return
*/
void first_output(Btree tree)
{
if(tree==NULL)
return;
printf("%c\t",tree->data);
//递归遍历左孩子
first_output(tree->lchild);
//递归遍历右孩子
first_output(tree->rchild);
}
/*
* function: 中序遍历
* @param [ in]
* @param [out]
* @return
*/
void mid_output(Btree tree)
{
if(tree==NULL)
return;
//递归遍历左孩子
mid_output(tree->lchild);
printf("%c\t",tree->data);
//递归遍历右孩子
mid_output(tree->rchild);
}
/*
* function: 后续遍历
* @param [ in]
* @param [out]
* @return
*/
void last_output(Btree tree)
{
if(tree==NULL)
return;
//递归遍历左孩子
last_output(tree->lchild);
//递归遍历右孩子
last_output(tree->rchild);
printf("%c\t",tree->data);
}
void Count(Btree tree,int *n0,int *n1,int *n2)
{
if(tree==NULL)
return;
if(tree->lchild==NULL && tree->rchild==NULL)
(*n0)++;//++*n0
else if(tree->lchild!=NULL && tree->rchild!=NULL)
(*n2)++;
else
(*n1)++;
Count(tree->lchild,n0,n1,n2);
Count(tree->rchild,n0,n1,n2);
}
int High(Btree tree)
{
if(tree==NULL)
return 0;
int left=High(tree->lchild)+1;
int right=High(tree->rchild)+1;
return left>right?left:right;
}
void free_space(Btree tree)
{
if(tree==NULL)
return ;
free_space(tree->lchild);
free_space(tree->rchild);
free(tree);
tree=NULL;
}
int main(int argc, const char *argv[])
{
//创建并输入,递归
Btree tree=create_tree();
//先序遍历:根左右
puts("first data is");
first_output(tree);
puts("\nmid data is");
mid_output(tree);
puts("\nlast data is");
last_output(tree);
int n0=0,n1=0,n2=0;
Count(tree,&n0,&n1,&n2);
printf("n0=%d n1=%d n2=%d\n",n0,n1,n2);
int h=High(tree);
printf("高度是:%d\n",h);
free_space(tree);
tree=NULL;
first_output(tree);
return 0;
}