dpdpdp

news2024/12/24 2:49:56

这里写目录标题

    • 139. 单词拆分
    • 322. 零钱兑换
    • 300. 最长递增子序列
    • 120. 三角形最小路径和
    • 64. 最小路径和
    • 63. 不同路径 II
    • 5. 最长回文子串（回文dp）⭐
    • 97. 交错字符串⭐（抽象成路径问题）
    • 221. 最大正方形⭐

139. 单词拆分

class Solution {
public:
    const int N=305;
    bool wordBreak(string s, vector<string>& wordDict) {
        vector<bool> dp(N,false);
        set<string> S;
        S.clear();
        for(int i=0;i<wordDict.size();i++){
            S.insert(wordDict[i]);
        }
        dp[0]=true;
        int n=s.size();
        for(int i=1;i<=n;i++){//从头开始长度为i的子串
            for(int j=0;j<i;j++){
                if(dp[j]){
                    string str=s.substr(j,i-1-(j-1));//0123
                    if(S.find(str)!=S.end()){
                        dp[i]=true;
                    }
                }
            }
            
        }
        return dp[n];
    }
};

322. 零钱兑换

class Solution {
public:
    const int inf=0x3f3f3f3f;
    int coinChange(vector<int>& coins, int amount) {
        vector<int> dp(amount+1,inf);
        // dp[i]表示凑出金额i最少需要的硬币个数
        dp[0]=0;
        int n=coins.size();
        for(int i=1;i<=amount;i++){
            for(int j=0;j<n;j++){
                if(i>=coins[j]){
                    dp[i]=min(dp[i],dp[i-coins[j]]+1);
                }
            }
        }
        if(dp[amount]==inf)return -1;
        else return dp[amount];
    }
};

恰好装满型完全背包

class Solution {
public:
    const int inf=0x3f3f3f3f;
    int coinChange(vector<int>& coins, int amount) {
        vector<int> dp(amount+1,inf);
        // dp[i]表示凑出金额i最少需要的硬币个数
        dp[0]=0;
        int n=coins.size();
         for(int j=0;j<n;j++){
            for(int i=coins[j];i<=amount;i++){

                if(i>=coins[j]){
                    dp[i]=min(dp[i],dp[i-coins[j]]+1);
                }
            }
        }
        if(dp[amount]==inf)return -1;
        else return dp[amount];
    }
};

300. 最长递增子序列

class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        int n=nums.size();
        vector<int> dp(n+5,1);
        // dp[0]=0;
        int res=1;
        for(int i=0;i<n;i++){//i是上升子序列最后一个元素的下标
            for(int j=0;j<i;j++){
                if(nums[i]>nums[j]){
                    dp[i]=max(dp[i],dp[j]+1);
                    res=max(res,dp[i]);
                }
                
            }
        }
        return res;
    }
};

贪心思想，碰到小的元素，尽可能放在前面
最后得到的最长上升子序列，假设存储在d数组中，d数组的演变过程：
来了个更大的元素（大于d[len]), 直接插入在末尾
如果小，找到大于nums[i] 的第一个元素，替换掉

class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        int n=nums.size();
        vector<int> d(n+5,1);
        int len=0;
        d[len]=nums[0];
        for(int i=1;i<n;i++){
            if(nums[i]>d[len]){
                d[++len]=nums[i];
            }
            else{//找到第一个大于nums[i]的d[k] 换掉
                int l=0,r=len;
                while(l<r){
                    int mid=(l+r)/2;
                    // if(d[mid]>nums[i])r=mid;
                    // else l=mid+1;找最大
                    // if(d[mid]<nums[i])r=mid;
                    // else l=mid+1;
                    if(d[mid]<nums[i])l=mid+1;
                    else r=mid;
                }
                d[l]=nums[i];
            }
        }
        return len+1;
    }
};

lower_bound,找到大于等于nums[i]的第一个元素

class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        int n=nums.size();
        vector<int> d;

        for(int i=0;i<n;i++){
vector<int>::iterator it =lower_bound(d.begin() , d.end() ,nums[i]);
if(it==d.end())d.push_back(nums[i]);
else
 swap(*it,nums[i]);
        }
        return d.size();
    }
};

120. 三角形最小路径和

倒三角形，注意下标

class Solution {
public:
    int minimumTotal(vector<vector<int>>& triangle) {
        int m=triangle.size();
        // int n=triangle[0].size();
        vector<vector<int> > dp(m,vector<int>(m,0));
        dp[0][0]=triangle[0][0];
        // int res=0x3f3f3f3f;
       int res=2e6+10;
        for(int i=1;i<m;i++){
           
            for(int j=0;j<=i;j++){
                 if(j==0)dp[i][j]=dp[i-1][j]+triangle[i][j];
                 else if(j==i)dp[i][j]=dp[i-1][j-1]+triangle[i][j];
                else dp[i][j]=min(dp[i-1][j-1],dp[i-1][j])+triangle[i][j];
                // if(i==m-1)res=min(res,dp[i][j]);怎么放在这儿就不行了why not？？？？？？
            }
            
        }
        //  res=*min_element(dp[m-1].begin(),dp[m-1].end());
    //    res=min(2000010,-10);
    for(int i=0;i<m;i++)res=min(res,dp[m-1][i]);
    return res;
    }
};

64. 最小路径和

class Solution {
public:
    int minPathSum(vector<vector<int>>& grid) {
        int m=grid.size();
        int n=grid[0].size();
        vector<vector<int>> dp(m,vector<int>(n,0));
        dp[0][0]=grid[0][0];
        for(int j=1;j<n;j++)dp[0][j]=dp[0][j-1]+grid[0][j];
        for(int i=1;i<m;i++){
            for(int j=0;j<n;j++){
                if(j==0)dp[i][j]=dp[i-1][j]+grid[i][j];
                else dp[i][j]=min(dp[i-1][j],dp[i][j-1])+grid[i][j];
            }
        }
        return dp[m-1][n-1];
    }
};

63. 不同路径 II

class Solution {
public:
    int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
        int m=obstacleGrid.size();
        int n=obstacleGrid[0].size();
        vector<vector<int>> dp(m,vector<int>(n,0));
        if(!obstacleGrid[0][0])dp[0][0]=1;
        for(int i=1;i<n;i++)if(!obstacleGrid[0][i])dp[0][i]=dp[0][i-1];
        for(int i=1;i<m;i++){
            for(int j=0;j<n;j++){
                if(!obstacleGrid[i][j])
                {
                    if(j==0)dp[i][j]=dp[i-1][j];
                    else dp[i][j]=dp[i-1][j]+dp[i][j-1];
                }
            }
        }
        return dp[m-1][n-1];
    }
};

5. 最长回文子串（回文dp）⭐

class Solution {
public:
    string longestPalindrome(string s) {
        int L=s.size();
        vector<vector<bool> > dp(L+1,vector<bool>(L+1,false));
        int maxlen=1;
        int pos=0;
        for(int len=1;len<=L;len++){
            for(int i=0;i+len-1<L;i++){
                int j=i+len-1;
                // dp[i][j]这段是否为回文串
                if(len==1)dp[i][j]=true;
                else{
                    if(s[i]==s[j]){
                        if(len==2||len==3){
                        dp[i][j]=true;
                        }
                        else {
                        dp[i][j]=dp[i+1][j-1];
                        }
                    }
                }
               if(dp[i][j]){
                   if(len>maxlen){
                       maxlen=len;
                       pos=i;
                   }
               } 
            }
        }
        // return s.substr(pos,maxlen);
        string res;
        for(int len=1;len<=L;len++){
            for(int i=0;i+len-1<L;i++){
                int j=i+len-1;
                if(dp[i][j])res=s.substr(i,len);
            }
        }
        return res;
    }
};

class Solution {
public:
    string longestPalindrome(string s) {
        int L=s.size();
        vector<vector<bool> > dp(L+1,vector<bool>(L+1,false));
        for(int i=0;i<L;i++)dp[i][i]=true;
        int pos=0;
        int maxlen=1;
        for(int len=2;len<=L;len++){
            for(int i=0;i+len-1<L;i++){
                int j=i+len-1;
                // dp[i][j]这段是否为回文串
                
               
                    if(s[i]==s[j]){
                        if(len==2||len==3){
                        dp[i][j]=true;
                        }
                        else {
                        dp[i][j]=dp[i+1][j-1];
                        }
                    }
               
               if(dp[i][j]){
                   maxlen=len;
                   pos=i;
               } 
            }
        }
        return s.substr(pos,maxlen);
        // string res;
        // for(int len=1;len<=L;len++){
        //     for(int i=0;i<L;i++){
        //         int j=i+len-1;
        //         if(dp[i][j])res=s.substr(i,len);
        //     }
        // }
        // return res;
    }
};

97. 交错字符串⭐（抽象成路径问题）

s1s2交错组成s3，把s1s2抽象为横纵坐标，s3抽象为向右向下的路径

class Solution {
public:
    bool isInterleave(string s1, string s2, string s3) {
        int m=s1.size();
        int n=s2.size();
        if(m+n!=s3.size())return false;// "" ,"" ,"a"
        vector <vector<bool> > dp(m+1,vector<bool>(n+1,false));
        // 一些最基础的子问题的初始化处理
        dp[0][0]=true;
        for(int len=1;len<=m;len++){
            if(s1[len-1]==s3[len-1])dp[len][0]=true;
            else break;
        }
        for(int len=1;len<=n;len++){
            if(s2[len-1]==s3[len-1])dp[0][len]=true;
            else break;
        }
        for(int i=1;i<=m;i++){
            for(int j=1;j<=n;j++){
                // dp[len1][len2] 
                // dp[len1-1][len2] s1[len1-1]==s3[len1+len2-1]
                if(s1[i-1]==s3[i+j-1])dp[i][j]=dp[i-1][j];
                if(s2[j-1]==s3[i+j-1])dp[i][j]=dp[i][j]||dp[i][j-1];
            }
        }
        return dp[m][n];
    }
};

221. 最大正方形⭐

本来应该用三维dp表示（正方形右下角的横纵坐标，第三维为 以该坐标为右下角的所有全1正方形边长），即dp[i][j][k]表示 以 （i,j）为右下角，边长为k的正方形是否存在
dp思想，是否存在由子问题的解递推而来，如果dp[i-1][j][k-1]，dp[i][j-1][k-1]，dp[i-1][j-1][k-1]三者都为true，则dp[i][j][k]为true

思路来呀
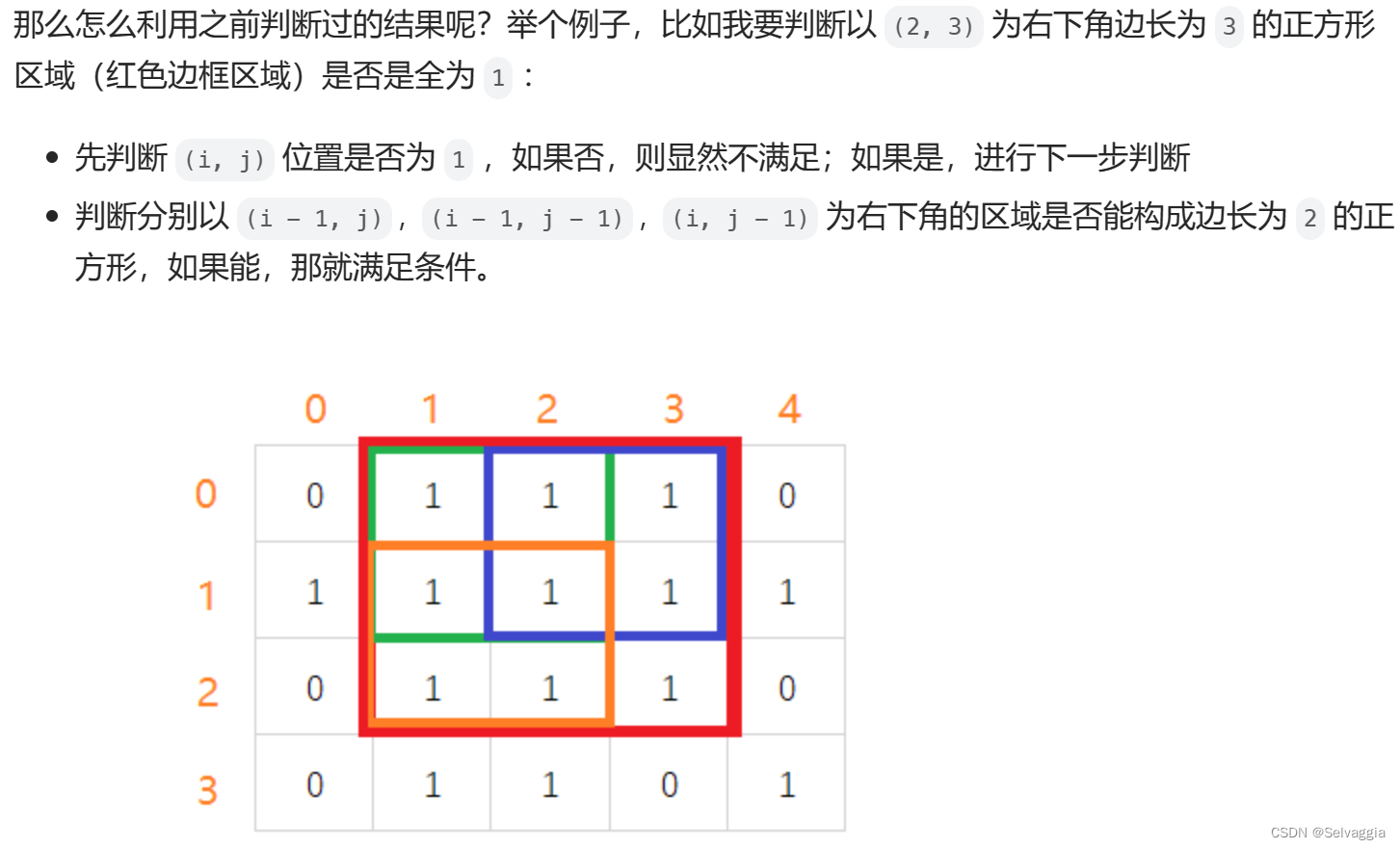
在这里插入图片描述

可以优化为两维，dp[i][j]的值为int型，表示 以该坐标为右下角的所有全1正方形之中最大的边长
比如 边长为3的全1正方形区域，那么它一定包含了一个边长为2和边长为1的全1正方形区域。所以，我们只需记录以(i, j)为右下角的区域包含的最大全1正方形边长即可，这个最大边长也即以(i , j)为右下角的全1正方形的个数

class Solution {
public:
const int N=305;
    int maximalSquare(vector<vector<char>>& matrix) {
        int m=matrix.size();
        int n=matrix[0].size();
        vector<vector<int>> dp(m+1,vector<int>(n+1,0));
        // vector<vector<vector<bool>>> dp(N,vector<vector<bool>>(N,vector<bool>(N,false)));
        int mx=0;
        for(int i=0;i<m;i++)if(matrix[i][0]=='1')dp[i][0]=1,mx=1;
        for(int i=0;i<n;i++)if(matrix[0][i]=='1')dp[0][i]=1,mx=1;
        for(int i=1;i<m;i++){
            for(int j=1;j<n;j++){
                if(matrix[i][j]=='1'){
                    dp[i][j]=min(min(dp[i-1][j-1],dp[i-1][j]),dp[i][j-1])+1;
                mx=max(mx,dp[i][j]);

                }
            }
        }
        return mx*mx;
    }
};

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/779326.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

实用便捷！一站式BI系统推荐

实用便捷！一站式BI系统推荐

在企业数字化转型过程中&#xff0c;BI系统可以建立业务、数据的双驱引擎&#xff0c;形成业务、数据的互补作用&#xff0c;通过建立数字化技术架构&#xff0c;明确企业的战略定位和业务目标&#xff0c;从而支撑实现这个目标。而一站式BI系统&#xff0c;则是指可以轻松从数…
阅读更多...
使用Soft-RoCE实践RDMA

使用Soft-RoCE实践RDMA

RDMA介绍 RDMA&#xff08; Remote Direct Memory Access &#xff09;意为远程直接地址访问&#xff0c;通过RDMA&#xff0c;本端节点可以“直接”访问远端节点的内存。所谓直接&#xff0c;指的是可以像访问本地内存一样&#xff0c;绕过传统以太网复杂的TCP/IP网络协议栈读…
阅读更多...
Github 上有没有优秀的Java 项目推荐？

Github 上有没有优秀的Java 项目推荐？

前言 下面是我精心整理的GitHub上关于Java的高Star的项目&#xff0c;可以自己选择去练手喔&#xff0c;希望对你有帮助~ 我们直接进入正题——> 1、 JavaGuide Star&#xff1a;135k JavaGuide指的是一份完整的Java学习指南或学习资料&#xff0c;它提供了Java编程语言…
阅读更多...
AcWing4118. 狗和猫

AcWing4118. 狗和猫

输入样例1&#xff1a; 3 6 10 4 0 CCDCDD 4 1 2 0 CCCC 4 2 1 0 DCCD输出样例1&#xff1a; Case #1: YES Case #2: YES Case #3: NO样例1解释 在 Case 1 中&#xff0c;一共有 1010 份狗粮和 44 份猫粮。 前两只动物是猫&#xff0c;喂食它们后&#xff0c;还剩下 22 份猫粮…
阅读更多...
数据结构之BinaryTree（二叉树）的实现

数据结构之BinaryTree（二叉树）的实现

BinaryTree要实现的方法 总结 remove不在BinNode里&#xff0c;而是BinTree里 递归的两种写法 从上往下&#xff1a;同一对象的递归&#xff08;参数多一个&#xff0c;判空用一句话&#xff09;&#xff0c;子对象的递归&#xff08;参数void&#xff0c;判空用两句话&#…
阅读更多...
算法分析和设计简答题

算法分析和设计简答题

算法分析和设计简答题 1.1分治法的算法思想&#xff08;重点&#xff09; 1.2动态规划的算法思想&#xff08;重点&#xff09; 1.3贪心算法的算法思想 1.4回溯算法的算法思想 1.5分支限界法的算法思想 1.6时间复杂度的定义(最好/一般/坏)&#xff0c;有什么意思 1.7渐进记号…
阅读更多...
【Git】分支合并冲突产生与解决

【Git】分支合并冲突产生与解决

文章学习自&#xff1a;麦兜搞IT&#xff0c;如有侵权&#xff0c;告知删除 文章目录 前言1 Fast Forword 合并1.1 核心原理1.2 举个栗子1.3 经验之谈 2 three way merge2.1 核心原理2.2 举个栗子&#xff08;不带冲突&#xff09;2.3 带冲突的three way merge 3 变基rebase3.…
阅读更多...
Windows上配置Python环境变量

Windows上配置Python环境变量

Python配置环境变量 &#x1f341;博主简介 &#x1f3c5;云计算领域优质创作者   &#x1f3c5;华为云开发者社区专家博主   &#x1f3c5;阿里云开发者社区专家博主 &#x1f48a;交流社区&#xff1a;运维交流社区 欢迎大家的加入&#xff01; Python下载官网&#xff1…
阅读更多...
GB28181设备接入端如何播放语音广播数据？

GB28181设备接入端如何播放语音广播数据？

技术背景 语音广播功能是GB28181设备接入端非常重要的功能属性&#xff0c;语音广播让终端和平台之间&#xff0c;有了实时双向互动&#xff0c;可以满足执法记录仪、智能安全帽、智能监控、智慧零售、智慧教育、远程办公、明厨亮灶、智慧交通、智慧工地、雪亮工程、平安乡村、…
阅读更多...
arm-day4

arm-day4

阅读更多...
Docker介绍以及实战教程

Docker介绍以及实战教程

Docker简介 Docker为什么出现 从事软件开发的朋友&#xff0c;可能经常会碰到以下场景&#xff1a;运维&#xff1a;你这程序有Bug啊&#xff0c;怎么跑不起来啊&#xff01;开发&#xff1a;我机子上能跑啊&#xff0c;你会不会用啊究其原因还是开发环境与生产环境不同造成的…
阅读更多...
基于linux下的高并发服务器开发（第二章）- 2.18 内存映射（2）

基于linux下的高并发服务器开发（第二章）- 2.18 内存映射（2）

1.如果对mmap的返回值(ptr)做操作(ptr), munmap是否能够成功? void * ptr mmap(...);ptr; 可以对其进行操作munmap(ptr, len); // 错误,要保存地址 2.如果open时O_RDONLY, mmap时prot参数指定PROT_READ | PROT_WRITE会怎样? 错误&#xff0c;返回MAP_FAILEDopen()函数中的…
阅读更多...
cpolar+calibre搭建自己的kindle书库

cpolar+calibre搭建自己的kindle书库

cpolarcalibre搭建自己的kindle书库 在我们身边众多的便携电子设备中&#xff0c;Kindle无疑是最为矛盾的设备之一&#xff0c;很多人在买它时都想读书破万卷&#xff0c;可是到最后Kindle的归宿都是盖泡面。尽管如此&#xff0c;当亚马逊不讲武德&#xff0c;打算将Kindle真正…
阅读更多...
FPGA中RAM的结构理解

FPGA中RAM的结构理解

FPGA中RAM的结构理解 看代码的过程中对RAM的结构不是很理解&#xff0c;搞脑子一片浆糊&#xff0c;反复推算&#xff0c;好不容易理清了思路&#xff0c;记录下来&#xff0c;防止忘记。开辟的RAM总容量为128bytes&#xff0c;数据的位宽为32位&#xff08;即一个单元有32bit…
阅读更多...
CodeForces：Madoka and Underground Competitions

CodeForces：Madoka and Underground Competitions

经过观察&#xff0c;发现只要延小区域 右上-左下 的对角线填满X即可&#xff0c;那么就是可以总结为满足(i j) % k (r c) % k #include <bits/stdc.h> using namespace std; int t; void solve(){int n, k, r, c;cin >> n >> k >> r >> c…
阅读更多...
团队如何选择合适的Git分支策略？

团队如何选择合适的Git分支策略？

现代软件开发过程中要实现高效的团队协作&#xff0c;需要使用代码分支管理工具实现代码的共享、追溯、回滚及维护等功能。目前流行的代码管理工具&#xff0c;包括CVS&#xff0c;SVN&#xff0c;Git&#xff0c;Mercurial等。 相比CVS和SVN的集中管理&#xff0c;Git具有非常…
阅读更多...
【stable diffusion】保姆级入门课程03-Stable diffusion（SD）图生图-涂鸦(绘图)的用法

【stable diffusion】保姆级入门课程03-Stable diffusion（SD）图生图-涂鸦(绘图)的用法

目录 0.本章素材 1.涂鸦有什么用 2.涂鸦的使用场景是什么 3.操作面板 4.提示词与涂鸦 5.涂鸦与重绘幅度 6.涂鸦的其他用法(自由创作) 7.课后训练 0.本章素材 Realistic Vision V3.0模型(真实系模型)百度网盘链接&#xff1a;https://pan.baidu.com/s/1HkSKW2t4L6wMg…
阅读更多...
openlayers系列：加载arcgis和geoserver在线离线切片

openlayers系列：加载arcgis和geoserver在线离线切片

https://www.freesion.com/article/1751396517/ 1.背景 有个项目需要使用openlayer加载各种服务上发布的数据&#xff0c;坐标系也不同&#xff0c;我们都知道openalyer默认可以加载EPAG:3857,要加载4490的坐标系的数据需要重新定义一下&#xff0c;之后再加载。一想起要重新…
阅读更多...
[SQL系列] 从头开始学PostgreSQL 事务 锁 子查询

[SQL系列] 从头开始学PostgreSQL 事务 锁 子查询

[SQL系列] 从头开始学PostgreSQL 索引 修改 视图_Edward.W的博客-CSDN博客https://blog.csdn.net/u013379032/article/details/131818865 事务 事务是一系列逻辑相关的数据库操作&#xff0c;可以作为一个整体进行操作或者回滚。事务通常会包含一个序列的读或者写操作&#xf…
阅读更多...
No4: Python脚本的交互式运用

No4: Python脚本的交互式运用

No4: Python脚本的交互式运用 1、 先安装了Python和环境变量设置 2、编写Pthon脚本 3、在脚本所在目录位置下&#xff0c;Python 脚本&#xff1b;
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023