算法分析和设计简答题

1.1分治法的算法思想（重点）

1.2动态规划的算法思想（重点）

 

 1.3贪心算法的算法思想

 1.4回溯算法的算法思想

 1.5分支限界法的算法思想

 

 1.6时间复杂度的定义(最好/一般/坏)，有什么意思

 

 1.7渐进记号有什么意思

1.常见的渐进记号 

 

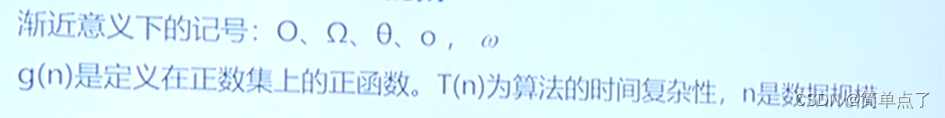
 2.意义
渐进记号（Asymptotic Notation）是用来描述算法时间复杂度的一种符号表示方法。它主要用于对算法的性能进行比较和分析，而不依赖于具体的输入规模或常数因子。
在算法的时间复杂度分析中，我们关注的是随着输入规模的增长，算法执行所需操作的增长速度。渐进记号提供了一种方式来表示算法的增长速度，使我们能够更好地理解和比较算法的效率。

1.8回溯和分支限界如何表示成一个解空间，如何画解空间

子集树和排列树

回溯算法和分支限界算法都是通过搜索解空间来寻找问题的解。解空间是指所有可能的解的集合，可以看作是一个多叉树的结构，其中每个节点表示问题的一个可能状态，路径表示选择或决策的序列，叶子节点表示一个有效的解。
下面分别介绍如何表示回溯算法和分支限界算法的解空间，并给出简单示例的解空间图。
1.    回溯算法的解空间表示：
a.    解空间中的每个节点表示问题的一个可能状态。
b.    从根节点开始，每次选择一个可行的决策，并递归地生成下一个状态。
c.    如果当前状态满足问题的约束条件，则向下搜索；如果不满足约束条件，则回溯到上一个状态进行其他选择。
d.    当达到叶子节点时，检查是否得到一个有效的解。
示例：回溯算法求解全排列问题（以[1,2,3]为例）
Copy Code
                      []
          /       |         \
       [1]      [2]       [3]
     /   \     /   \      /   \
  [1,2] [1,3] [2,1] [2,3] [3,1] [3,2]
     |       |        |        |
 [1,2,3] [1,3,2]  [2,1,3] [2,3,1] [3,1,2] [3,2,1]
2.    分支限界算法的解空间表示：
a.    解空间中的每个节点表示问题的一个可能状态。
b.    通过优先队列或优先级队列管理搜索分支，根据当前最优解估计值进行排序。
c.    对当前最优分支进行扩展，并生成新的状态。
d.    剪枝函数判断新状态是否可行或能够得到更优解，从而决定是否继续搜索该分支。
示例：分支限界算法求解0/1背包问题（以4个物品和背包容量为10为例）
Copy Code
                             []
                 /               |             \
        [0,0,0,0,0]        [0,0,1,0,0]       [0,0,0,1,0]
          /         \           |                |
[0,0,0,1,0]  [0,0,0,0,1] ---剪枝--- [0,1,0,0,0] [0,0,0,0,1]
在示例中，方括号表示一个状态，括号内的数字表示该状态下每个元素的取值。通过逐步选择或决策，并不断生成新的状态，最终达到一个叶子节点，即得到一个有效的解。
画解空间图有助于理解问题的解空间结构，帮助我们更好地分析算法的执行过程和优化策略，并进行问题的建模和求解。