一、说明
在进行优化回归过程,首先要看看是否存在最优策略?
在有限马尔可夫决策过程 (MDP) 中,最优策略被定义为同时最大化所有状态值的策略¹。换句话说,如果存在最优策略,则最大化状态 s 值的策略与最大化状态 值的策略相同。² 但为什么要有这样的政策呢?
萨顿和巴托关于强化学习的著名入门书¹认为最优策略的存在是理所当然的,而这个问题没有得到解答。我很难相信他们并能够继续阅读!
在本文中,我将证明有限 MDP ³ 中存在最优策略。
二、符号和定义
2.1 马尔可夫决策过程和政策
有限 MDP 的特征在于一组有限的状态(通常用曲线 S 表示),每个状态的一组有限动作(通常用曲线 A 表示),以及立即奖励值 r 和下一个状态 s' 的概率分布,给定当前状态 s 和当前选择的动作 a,表示为 p(s', r|s,a)。
给定当前状态 s,策略π是状态 s 上可能操作的概率分布,表示为 π(a|s)。 然后,给定一个策略,代理可以在环境中导航(即从一个状态转到另一个状态)并通过每个转换获得奖励。
我们用大写字母显示随机变量,用小写字母显示它们的值。时间用下标添加到每个变量中。然后,给定策略和 MDP,并给定初始状态(时间 t=1)s,对于任何 T > 1,状态、操作和奖励值的联合分布为
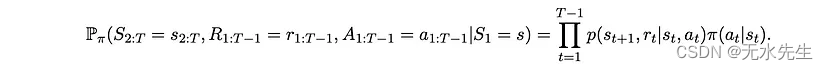
2.2 值和贝尔曼方程
给定策略π和折扣因子 0 ≤ γ < 1,每个状态的值定义为
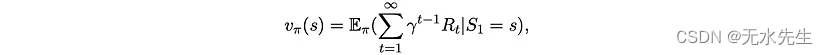
以及每对状态和操作的值为
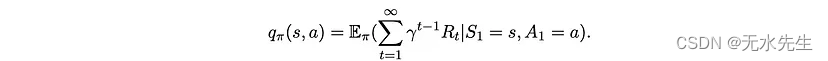
很容易证明状态和动作-状态对的值可以用递归方式编写
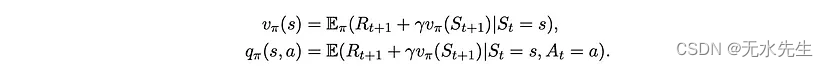
这些方程组被称为贝尔曼方程。
我们稍后将使用以下事实:
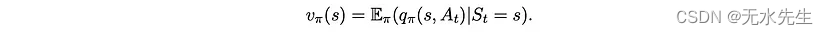
2.3 最佳策略
策略π*是最佳策略,当且仅当我们有
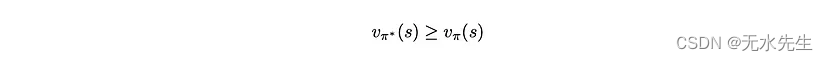
对于任何状态和任何其他策略π。
三、贝尔曼最优性方程
我们用曲线 S 显示所有可能状态的集合,用曲线 A 显示状态 s 处所有可能动作的集合。我们用δ表示克罗内克三角洲,并用以下定理开始本节。
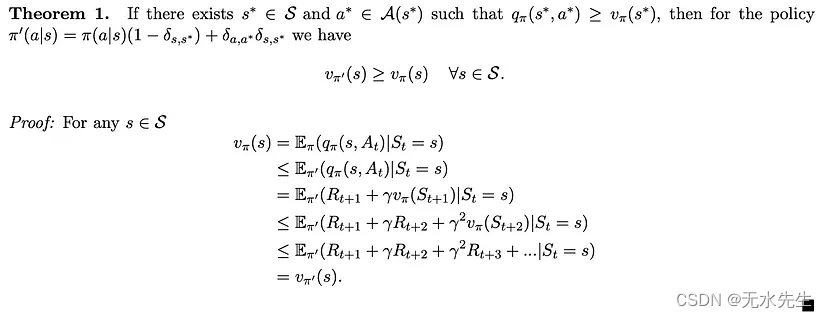
证明注释:我们在证明的第一行中使用了方程 1,然后反复使用了状态和动作对的值 (s*, a*) 大于或等于状态 s* 的值的事实。
定理 1 指出,就策略π而言,只要有一对状态和操作 (s*, a*) 的值大于状态 s* 的值,那么就所有状态而言,就会有另一个策略π优于或等于(就状态值而言)π。因此,如果存在最优策略 π*,则对于任何状态 s,其值应满足
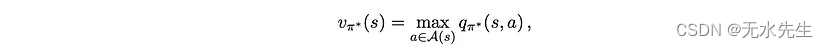
其中弯曲的 A(s) 代表状态 s 处所有可能动作的集合——人们可以很容易地通过矛盾来证明这个陈述。 使用贝尔曼方程,我们可以将方程2展开为:
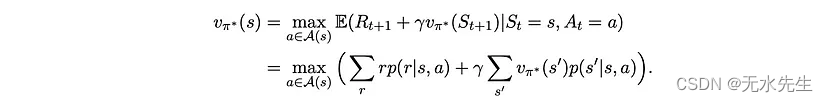
这组非线性方程(与状态数一样多)被称为“贝尔曼最优方程”。因此,如果存在最优策略,则其值应满足这组方程⁴。
因此,要证明最优策略的存在,必须证明以下两个陈述:
- 贝尔曼最优方程的集合有解,并且
- 其其中一个解决方案的值大于或等于所有状态下其他解决方案的值。
四、解决方案的存在和独特性
在本节中,我们证明了贝尔曼最优方程的集合具有唯一的解。通过这样做,我们同时证明了上述两个陈述。
4.1 贝尔曼最优运算符
给定一组状态上的值,我们将值的向量定义为
![]()
它只是一个实值向量,其元素等于不同状态的值。然后,我们将“贝尔曼最优算子”T定义为映射
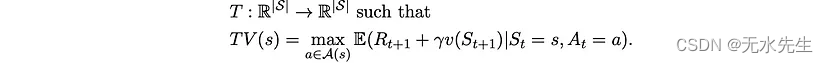
运算符 T 获取一个值向量并将其映射到另一个值向量。使用这种新符号,很容易看出等式 2 和 3 等价于
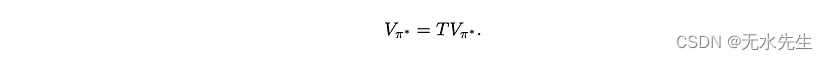
这一观察意味着贝尔曼最优性方程的解与贝尔曼最优性算子的不动点s 相同。因此,为了证明贝尔曼最优方程解的存在性和唯一性,可以证明贝尔曼最优性算子具有唯一的不动点。
为此,我们需要引入另一个概念和另一个定理。
4.2 收缩映射和巴拿赫不动点定理
考虑一个度量空间 (M,d),即 M 是一个集合,d 是在此集合上定义的度量,用于计算 M ⁵ 中每两个元素的距离。 映射 T:M → M 是一个收缩映射,如果存在 0 ≤ k < 1,对于 M 中的任何 x 和 y,我们有
![]()
直观地说,收缩映射使点彼此更近。图 1 显示了在两个点上重复应用收缩映射的图示。

我们对收缩映射感兴趣的原因是以下著名的定理,称为巴拿赫不动点定理。

证明注释: 定理的证明并不难,但我不把它包括在本文中,因为这个定理是众所周知的,证明可以很容易地在其他地方找到,例如见这里。
该定理背后的整个思想如图 1 所示:映射后所有点彼此靠近,因此,通过重复映射,所有点都收敛到一个点,即 T 的唯一不动点。
因此,为了证明贝尔曼最优性方程解的存在性和唯一性,足以证明存在一个度量,其中贝尔曼最优性算子是收缩映射。
4.3 贝尔曼最优算子是无穷范数中的收缩映射
对于任何一对值向量 V 和 V',它们的无穷范数定义为
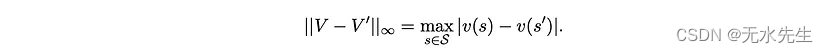
在本节中,我们要证明贝尔曼最优性算子是这个范数中的收缩映射。为此,我们首先需要以下引理。
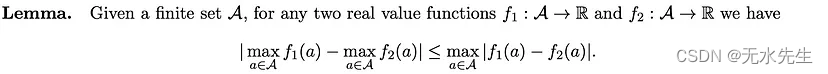
证明注释: 虽然引理不是平凡的,但它的证明并不困难,只需要基本的技术。我有一些乐趣证明它,并认为将其证明作为感兴趣的读者的练习可能会很好⁶。
现在,有了引理,我们终于可以进入我们的主定理了。

证明注释: 为了从证明的第 2 行到第 3 行,我们使用引理,从第 4 行转到第 5 行,我们使用绝对值函数的凸性。其余的都很简单。
因此,贝尔曼最优性算子具有唯一的不动点⁷,而贝尔曼最优性方程具有唯一的解。很容易证明,任何关于贝尔曼最优方程解的贪婪策略都具有等于该解的值。因此,存在最优策略!
五、结论
我们证明了(1)最优策略的值应该满足贝尔曼最优方程。然后,我们证明了(2)贝尔曼最优方程的解是贝尔曼最优性算子的不动点。通过证明(3)贝尔曼最优算子是无穷范数中的收缩映射,并使用(4)巴拿赫不动点定理,我们证明了(5)贝尔曼最优算子具有唯一的不动点。因此,(6)存在同时最大化所有州价值的政策。
参考和引用:
有限MDP最优策略存在的证明 :
阿里雷扎·莫迪尔沙内奇