Q1：2784. 检查数组是否是好的

https://leetcode.cn/problems/check-if-array-is-good/description/
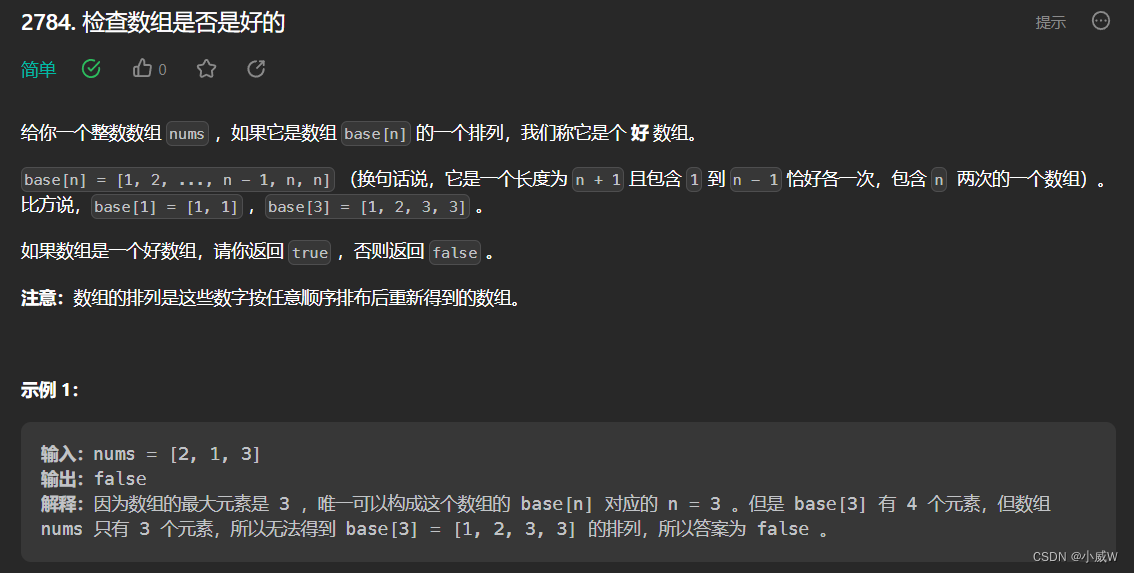
在这里插入图片描述
提示：

1 <= nums.length <= 100
1 <= num[i] <= 200

解法1——排序+模拟判断

class Solution {
    public boolean isGood(int[] nums) {
        Arrays.sort(nums);
        int n = nums.length - 1;
        for (int i = 0; i < n; ++i) {
            if (nums[i] != i + 1) return false;
        }
        return nums[n] == n;
    }
}

解法2——哈希表计数+模拟判断

在这里插入代码片

Q2：6926. 将字符串中的元音字母排序

https://leetcode.cn/problems/sort-vowels-in-a-string/

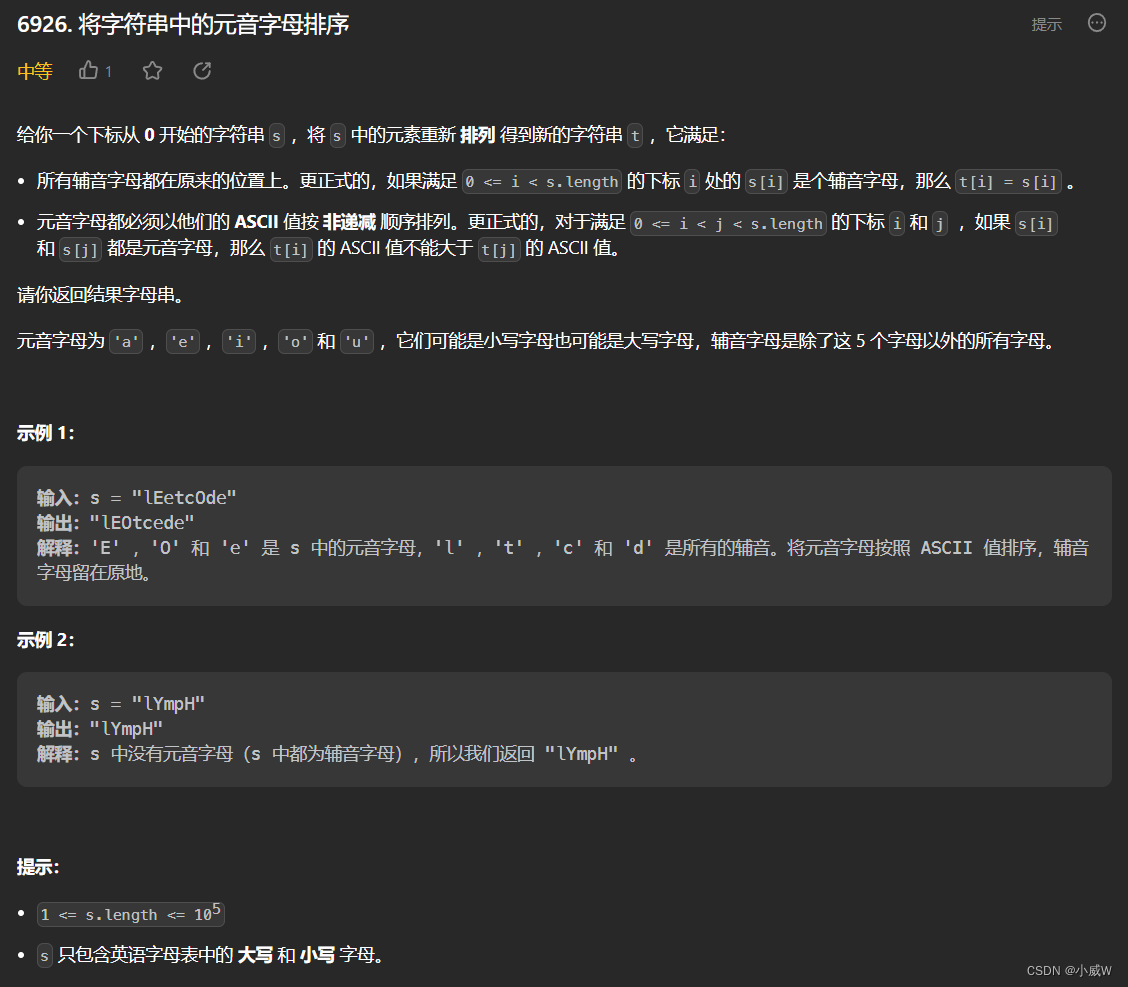
在这里插入图片描述

class Solution {
    public String sortVowels(String s) {
        List<Character> ls = new ArrayList<>();
        List<Integer> idxs = new ArrayList<>();
        int n = s.length();
        Set<Character> set = new HashSet<>(){{
            add('a');
            add('e');
            add('i');
            add('o');
            add('u');
            add('A');
            add('E');
            add('I');
            add('O');
            add('U');
        }};
        char[] chs = s.toCharArray();
        for (int i = 0; i < n; ++i) {
            if (set.contains(chs[i])) {
                ls.add(chs[i]);
                idxs.add(i);
            }
        }
        Collections.sort(ls);
        for (int i = 0; i < ls.size(); ++i) {
            chs[idxs.get(i)] = ls.get(i);
        }
        return new String(chs);
    }
}

哈希表还可以使用

Set<Character> set = new HashSet<>(Arrays.asList('a', 'e', 'i', 'o', 'u', 'A', 'E', 'I', 'O', 'U'));

或者使用 String 配合 .indexOf() 来代替哈希表。

Q3：6931. 访问数组中的位置使分数最大（线性DP）

https://leetcode.cn/problems/visit-array-positions-to-maximize-score/
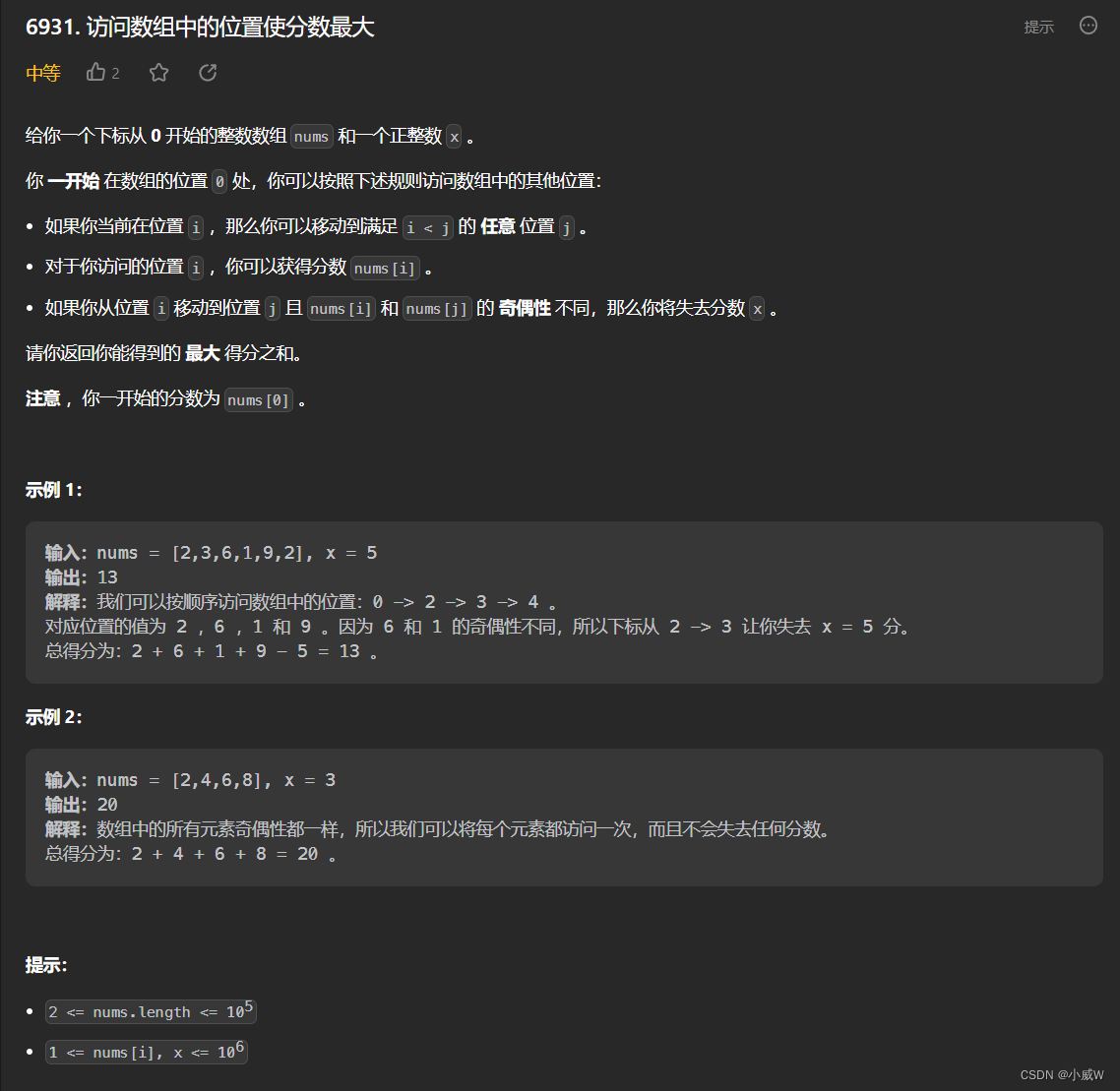
在这里插入图片描述

分奇偶 DP。

初始值设置成 -x 是为了抵消奇偶性不同时 -x 带来的影响。

class Solution {
    public long maxScore(int[] nums, int x) {
        int n = nums.length;
        long even = -x, odd = -x;
        if (nums[0] % 2 == 0) even = nums[0];
        else odd = nums[0];
        for (int i = 1; i < n; ++i) {
            if (nums[i] % 2 == 0) even = Math.max(even, odd - x) + nums[i];
            else odd = Math.max(odd, even - x) + nums[i];
        }
        return Math.max(even, odd);
    }
}

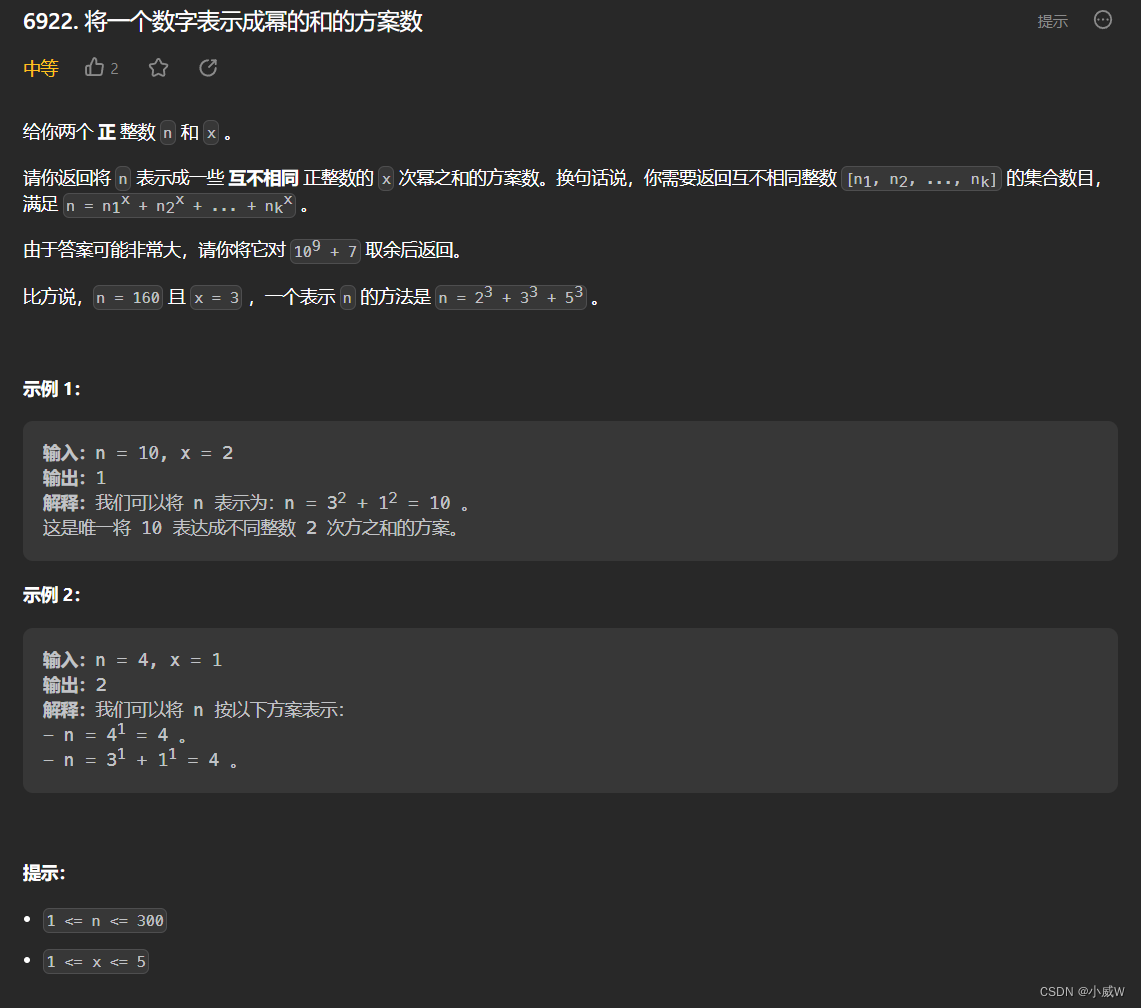
Q4：6922. 将一个数字表示成幂的和的方案数（01背包）

https://leetcode.cn/problems/ways-to-express-an-integer-as-sum-of-powers/

在这里插入图片描述

class Solution {
    public int numberOfWays(int n, int x) {
        int[] dp = new int[n + 1];
        dp[0] = 1;
        final int mod = (int)1e9 + 7;
        for (int i = 1, k = (int)Math.pow(i, x); k <= n; ++i, k = (int)Math.pow(i, x)) {
            for (int j = n; j >= k; --j) {
                dp[j] = (dp[j] + dp[j - k]) % mod;
            }
        }
        return dp[n];
    }
}