实验四  回溯法

售货员问题

1.实验内容

1、理解回溯法的深度优先搜索策略，掌握用回溯法解题的算法框架
2、设计并实现旅行售货员问题问题，掌握回溯算法。
 

2.实验环境

Java

3.问题描述

旅行售货员问题：设有一个售货员从城市1出发，到城市2，3，…，n去推销货物，最后回到城市1。假定任意两个城市i，j间的距离dij(dij=dji)是已知的，问他应沿着什么样的路线走，才能使走过的路线最短?

4.复杂度分析

回溯算法的时间复杂度主要取决于状态空间的大小，即可能的路径数量。在旅行售货员问题中，有n个城市，因此可能的路径数量为n!。每个路径都需要遍历n个城市。因此，回溯算法的时间复杂度为O(n!)。

5.代码实现

package shiyan4;

import java.io.File;
import java.io.FileWriter;
import java.io.IOException;
import java.util.ArrayList;
import java.util.List;
import java.util.Scanner;

public class TSPBacktracking {
    private static int[][] distanceMatrix;
    private static int numCities;
    private static List<Integer> bestPath;
    private static int shortestDistance;

    public static void main(String[] args) {
        readInputFromFile("input.txt");
        solveTSP();
        writeOutputToFile("output.txt");
    }

    private static void readInputFromFile(String filename) {
        try {
            File file = new File(filename);
            Scanner scanner = new Scanner(file);

            numCities = scanner.nextInt();
            distanceMatrix = new int[numCities][numCities];

            for (int i = 0; i < numCities; i++) {
                for (int j = 0; j < numCities; j++) {
                    distanceMatrix[i][j] = scanner.nextInt();
                }
            }

            scanner.close();
        } catch (IOException e) {
            e.printStackTrace();
        }
    }

    private static void solveTSP() {
        bestPath = new ArrayList<>();
        shortestDistance = Integer.MAX_VALUE;

        List<Integer> path = new ArrayList<>();
        path.add(0);  // Start from city 1

        backtrack(path, 0, 0);
    }

    private static void backtrack(List<Integer> path, int currentCity, int currentDistance) {
        if (path.size() == numCities) {
            // All cities have been visited, check if it forms a shorter path
            int totalDistance = currentDistance + distanceMatrix[currentCity][0]; // Distance back to city 1

            if (totalDistance < shortestDistance) {
                shortestDistance = totalDistance;
                bestPath = new ArrayList<>(path);
            }
            return;
        }

        for (int nextCity = 0; nextCity < numCities; nextCity++) {
            if (!path.contains(nextCity)) {
                path.add(nextCity);
                int distance = currentDistance + distanceMatrix[currentCity][nextCity];

                if (distance <= shortestDistance) {
                    backtrack(path, nextCity, distance);
                }

                path.remove(path.size() - 1);
            }
        }
    }

    private static void writeOutputToFile(String filename) {
        try {
            FileWriter writer = new FileWriter(filename);
            writer.write("Shortest distance: " + shortestDistance + "\n");
            writer.write("Best path: ");
            for (int city : bestPath) {
                writer.write((city + 1) + " "); // Adjust to 1-based index for cities
            }
            writer.close();
            System.out.println("输出成功！");
        } catch (IOException e) {
            e.printStackTrace();
        }
    }
}

输入

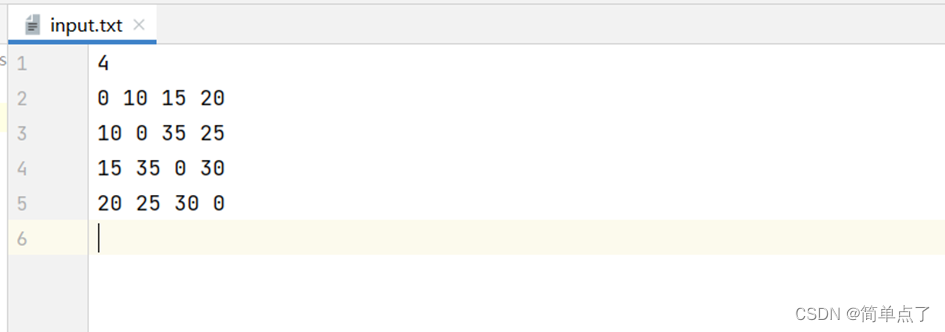
运行：

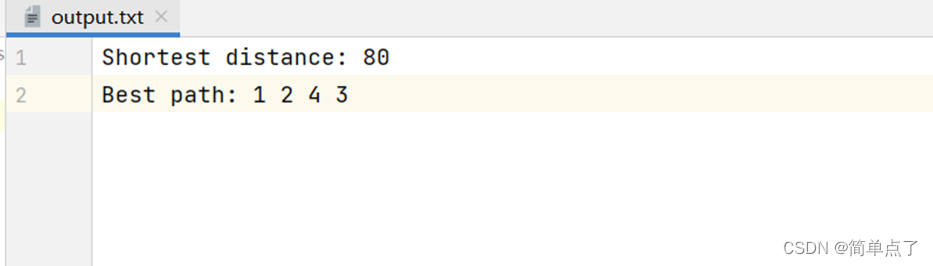
 输出