1.4 算法的时间复杂度

1.4.1 渐近时间复杂度

一般情况下，算法中基本操作重复执行的次数是问题规模n的某个函数f(n)，算法的时间量度记作T（n)=O(n)，它表示随问题规模n的增大而增大，算法执行时间的增长率和f(n)的增长率相同，称作算法的渐近时间复杂度，简称时间复杂度。

大O表示“同阶”，同等数量级。即：当 n->∞时，二者之比为常数

1.4.2 常对幂指阶

表示图

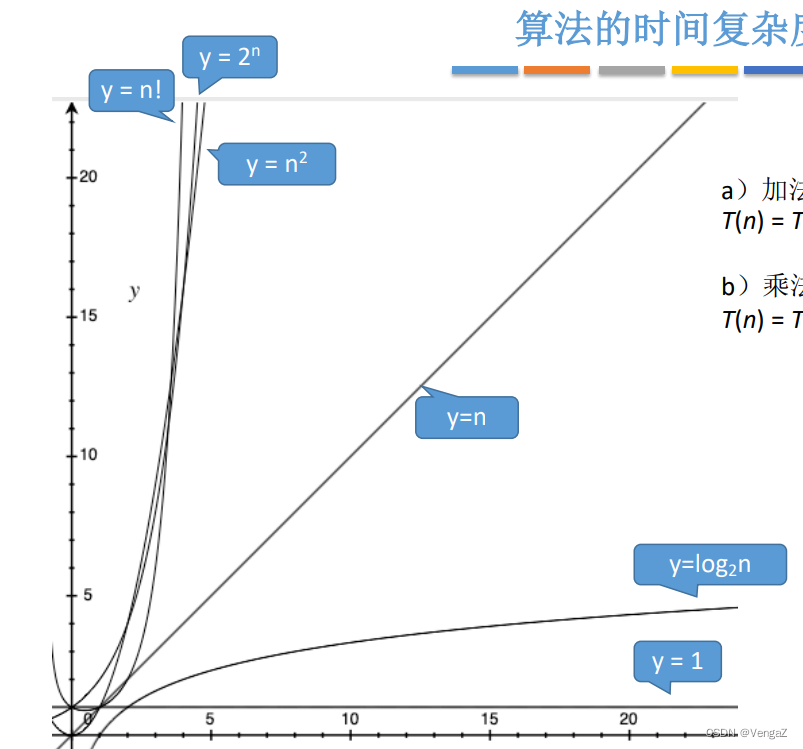
1.4.3 时间复杂度的计算

• 顺序执行的代码只会影响常数项，可以忽略
• 挑选循环中的一个基本操作分析执行次数与n的关系即可
• 对于多层嵌套循环，只需要关注最深层的循环（嵌套最深的，即将每个循环执行次数相乘）

1.4.4 最好与最坏时间复杂度

1.5 算法的空间复杂度

1.5.1 空间复杂度

• 无论问题规模怎么变换，算法与运行所需的内存空间都是固定的常量，则空间复杂度为S(n) = O(1)
• 在计算空间复杂度时，只需关注存储空间大小与问题规模相关的变量

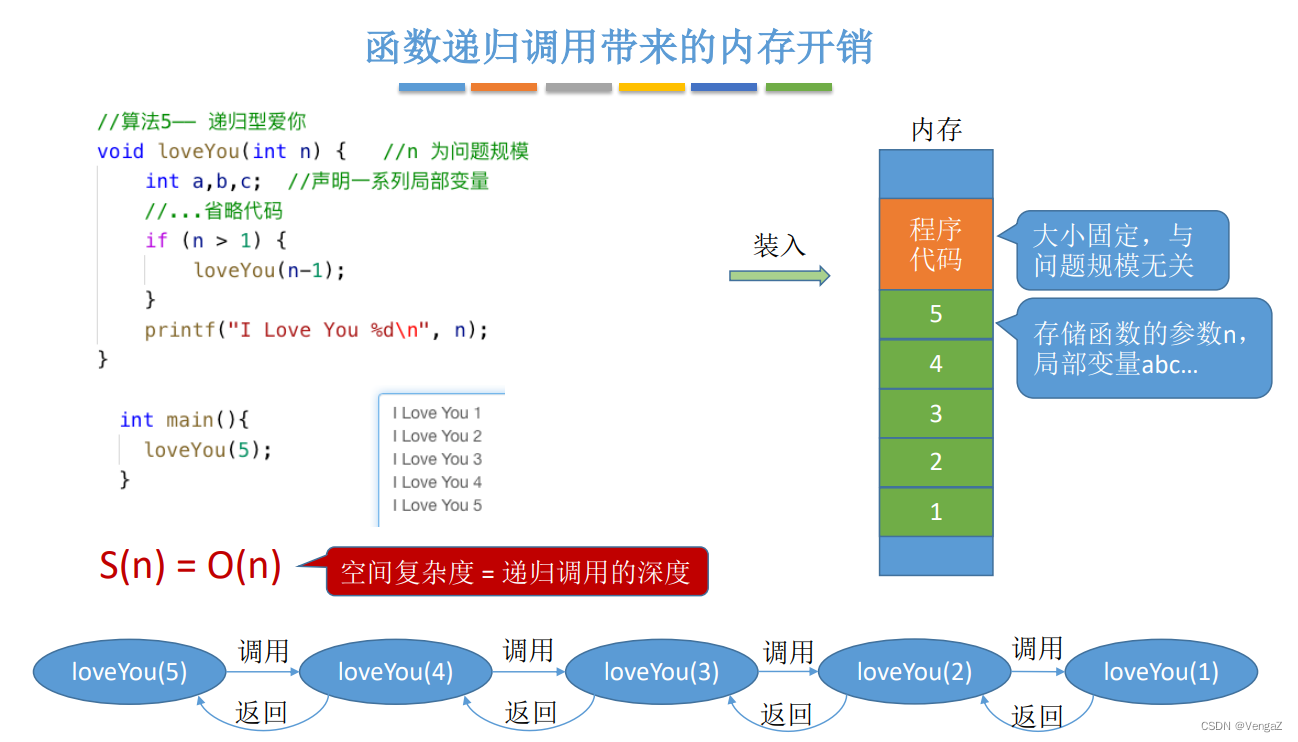
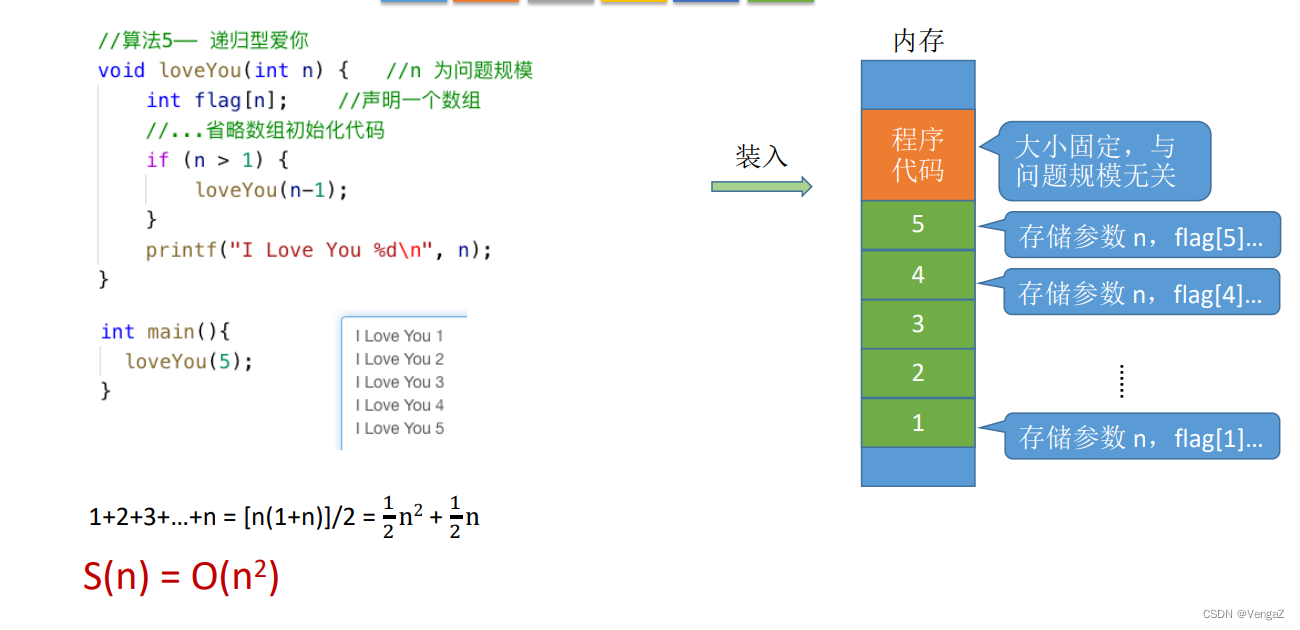
1.5.2 函数递归调用（未总结）

参考链接: 函数调用栈

1.5.3 存储地址

1.5.3.1 内存高低地址与高低位

参考: 内存高地址与低地址、变量的高位和低位

大端法就是，数据的前部（对于int型就是数据的高位）存在低地址

1.5.3.2 用户程序虚拟地址空间分布

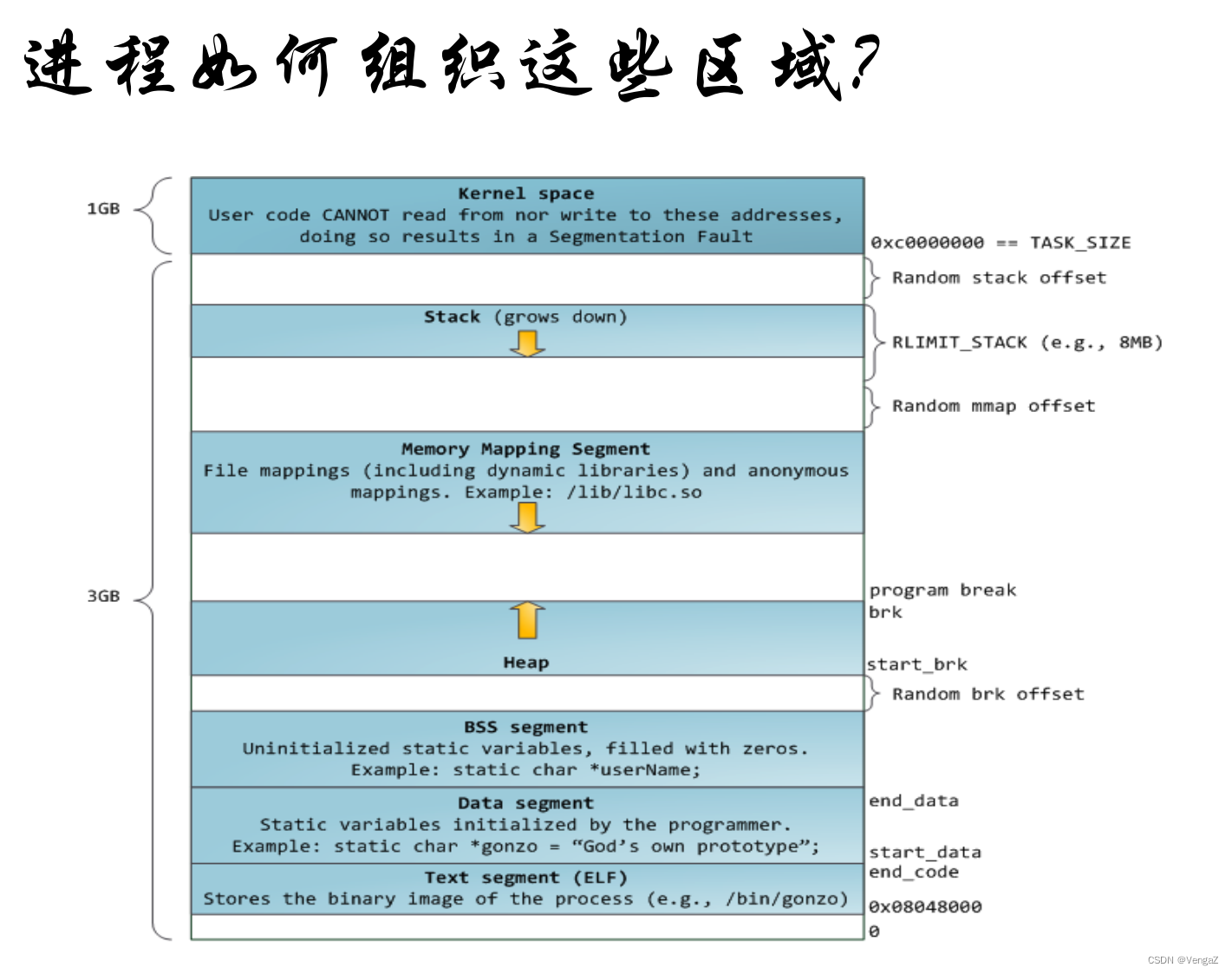
Eg：分析代码中的常量、 变量所属的段

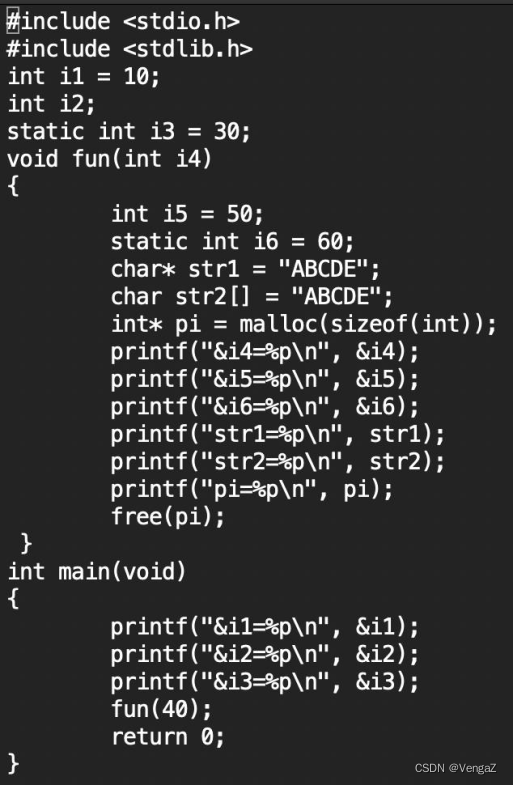
本地编译结果

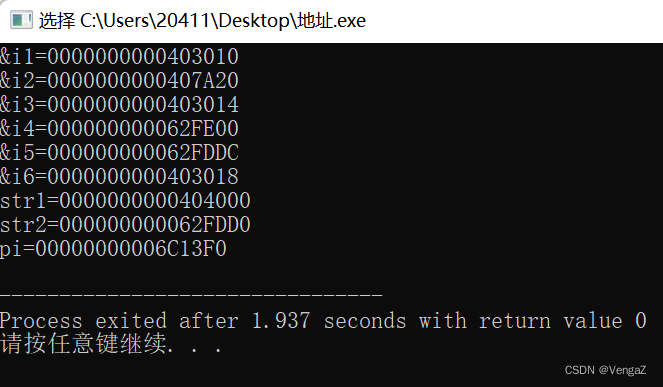
结果分析：

• i1是已经初始化的全局变量，故i存于数据段，且类型为int，四字节三十二位。
• i2是未初始化的全局变量，未设置初始值故为0（BSS段全部置零），类型为int，且由于BSS段在数据段上方，故i2（407A20）地址大于i1（403010）。
• i3是已经初始化的静态全局变量，所以i3存于数据段，类型为int，并且因为在i1之后声明，所以i3（403014）的地址高于i1（403010）的地址四个字节。
• i4是在fun（）里定义的局部变量，所以至于该函数的栈，且栈段位于最上方，所以i4的地址大于之前定义的i1 i2 i3。
• i5同i4是位于fun（）里定义的局部变量，所以i5同样位于栈段，由于栈段是向下延申的，所以i5（62FDDC）的地址小于i4（62FE00）的地址。
• i6是在fun（）里声明的静态局部变量，所以位于数据段，又因为是在i3之后声明在数据段里的所以i6（403018）地址比i3（403014）高四个字节。
• Str1是在fun（）里声明的局部指针变量char*，所以str1变量本身存放在栈段，但是变量中指向的字符串常量”ABCDE”地址，因此%P的形式打印出来的是str1（40400）所存储字符串的地址，所以打印出来的是一个位于数据段地址。又因为在i6（403018）之后声明，所以地址高于i6。
• Str2是在fun（）里声明的局部变量，所以位于栈段，且因为栈段向下延申，所以str2（62FDD0）的地址小于i5（62FDDC）的地址。
• Pi是在fun（）里声明的局部指针变量，并且为它分配了空间，指针本身位于栈段，但是它不同于str1，str1所指向的是位于数据段里的字符串”ABCDE”的地址。它指向malloc动态申请的地址空间，申请的空间位于堆段，所以%P打印出来的是位于堆段的地址，所以地址位于BSS段与栈段之间。