如下图所示，概率论与数理统计浙大第四版有如下例题：
简单说就是：已知两个相互独立工作电子装置寿命的概率密度函数，将二者串联成整机，求整机寿命的数学期望。

这个题目解答中的微积分部分可谓是相当的坑爹，根本没有任何中间计算过程，任何人直接看根本看不懂！所以说它是烂教材，根本不足为过！而国内确实有很多这种垃圾教材，写的不清不楚，误人子弟！

好了，说了这么多该进入正题了，其实这个里面的微积分计算有很大的难度和分析工作量，我下面来具体解释求解细节：

1. 首先第一，因为这两个电子装置是串联在一起的，当发生故障时：只要有一个坏了，整机就不能工作了！
   所以，整机的寿命必然取决于寿命最短的那一个，即
   整机寿命的概率分布函数 F(N) = Min(F(X1), F(X2))
   根据多维随机变量的概率分布公式（见第三章公式5.12），可得
   Fmin = 1 - [ 1- F(X) ][ 1 - F(Y) ] // 二维随机变量的情况
   而X1, X2这两个电子装置是相互独立的，而且它们的概率密度函数都是一样的
   所以可以得出：
   $$F(N)=Min(F(X1),F(X2))=1-[1-F(X){]}^2(1.1)$$

2. 要求出F(N),就得求出F(X)也就是电子装置的概率分布函数
   而概率分布函数是概率密度函数的积分
   所以
   F(X) = ${\int }_0^{\infty }f(x)dx$ = ${\int }_0^{\infty }\frac{1}{\theta }.e^{-x/\theta }dx$
   根据基本积分公式：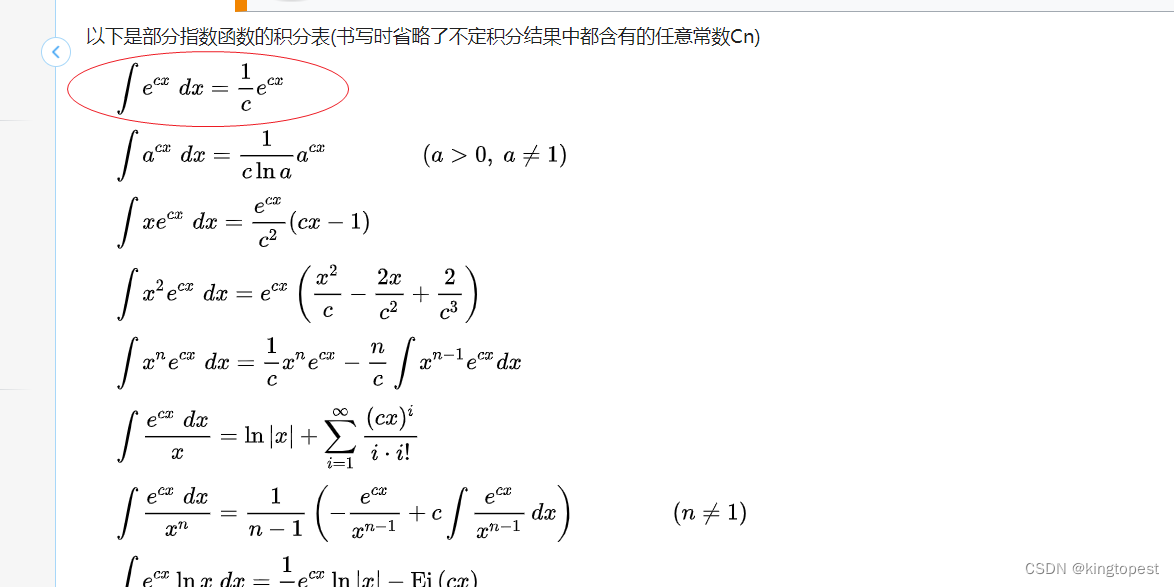
   上式可得(因为x<0时,f(x)=0,那么它的积分也为0，故只取大于0的积分)：
   F(X) = ${\int }_0^{\infty }\frac{1}{\theta }.e^{-x/\theta }dx$ = $\frac{1}{\theta }{\int }_0^{\infty }{e}^{(-\frac{1}{\theta }).x}dx$
   $=\frac{1}{\theta }\ast (-\theta )\ast .e^{-x/\theta }$ = $-e^{-x/\theta }{|}_0^{\infty }$
   $=-e^{-\infty /\theta }-(-e^{-0/\theta })=1-e^{-\infty /\theta }$
   可以看到这个积分并不是收敛的，所以只能把它变成变上限积分，于是
   $$F(X)=1-e^{-x/\theta }$$

3. 然后代入到前面的F(N)公式(1.1)中
   $$F(N)=1-[1-(1-e^{-x/\theta }){]}^2=1-e^{-2x/\theta }$$

4. 然后对F(N)求导获得f(N) 也就是整机的概率密度函数
   $$f(N)=(F(N){)}^{{}^{\prime }}=(-\frac{2}{\theta })(-e^{-2x/\theta })=\frac{2}{\theta }.e^{-2x/\theta }$$

5. 然后根据连续随机变量的数学期望公式：
   $$E(X)={\int }_{-\infty }^{+\infty }x.f(x)dx$$
   $$E(N)={\int }_{-\infty }^{+\infty }x.f(N)dx={\int }_{-\infty }^{+\infty }x.\frac{2}{\theta }.e^{-2x/\theta }dx$$
   $$=\frac{2}{\theta }.(-\frac{\theta }{2}{)}^2.{\int }_{-\infty }^{+\infty }(-\frac{2x}{\theta }).e^{-2x/\theta }d(-\frac{2x}{\theta })$$
   $$=\frac{\theta }{2}.{\int }_{-\infty }^{+\infty }(-\frac{2x}{\theta }).e^{-2x/\theta }d(-\frac{2x}{\theta })(2.1)$$
   根据分部积分公式：
   
   
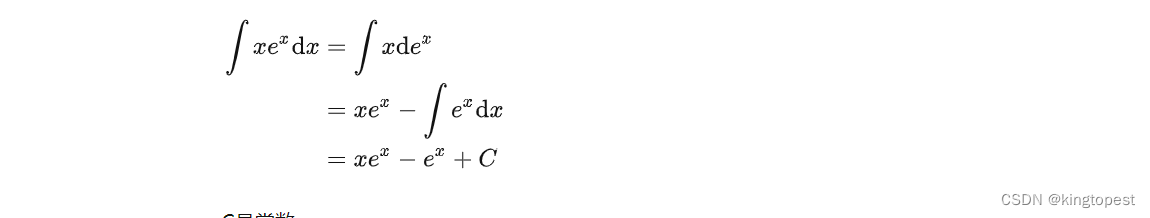
   可以推导出：
   $$\int x.e^{x}dx=x.e^x-e^x+C$$ 将此代入式（2.1）可得：

$$E(N)=\frac{\theta }{2}.[(-\frac{2x}{\theta }).e^{-2x/\theta }-e^{-2x/\theta }]{|}_{-\infty }^{+\infty }$$
但是F(N)在小于0时，积分为0，所以
$$E(N)=\frac{\theta }{2}.[(-\frac{2x}{\theta }).e^{-2x/\theta }-e^{-2x/\theta }]{|}_0^{+\infty }=-\frac{\theta }{2}.e^{-2x/\theta }.(1+\frac{2x}{\theta }){|}_0^{+\infty }$$
$$=-\frac{\theta }{2}.[\underset{x\to \infty }{\lim }(\frac{1+\frac{2x}{\theta }}{e^{2x/\theta }})-e^0.(1+\frac{0}{\theta })]$$
$$=\frac{\theta }{2}.[1-\underset{x\to \infty }{\lim }(\frac{1+\frac{2x}{\theta }}{e^{2x/\theta }})]$$
然后运用洛必达法则求极限:
$$E(N)=\frac{\theta }{2}.[1-\underset{x\to \infty }{\lim }\frac{(1+\frac{2x}{\theta }{)}^{{}^{\prime }}}{(e^{2x/\theta }{)}^{{}^{\prime }}}]=\frac{\theta }{2}.[1-\underset{x\to \infty }{\lim }\frac{\frac{2}{\theta }}{\frac{2}{\theta }.e^{2x/\theta }}]$$
$$=\frac{\theta }{2}.[1-\underset{x\to \infty }{\lim }\frac{1}{e^{2x/\theta }}]$$
很明显：在x->无穷大时，$\frac{1}{e^{2x/\theta }}$的极限为０
所以，最终 $E(N)=\frac{\theta }{2}$
即整机的数学期望$E(N)=\frac{\theta }{2}$
可以看到整个微积分的求解过程还是很复杂的，但是教材上却只是一带而过，让人相当无语，足见浙大概率论教材质量是非常坑爹的，需要自己仔细分析推导，才能得到正确结果。