👍作者主页:进击的1++
🤩 专栏链接:【1++的C++初阶】
文章目录
- 一,什么是适配器
- 二,栈与队列模拟实现
- 三,优先级队列
- 四,reverse_iterator
一,什么是适配器

适配器作为STL的六大组件之一,其本质是一种设计模式,将一个class的接口转换为另一个class的接口。比如说我们接下来要进行模拟实现的stack。若是以vector为底层,其实就是对vector接口的再次封装。因此其虽然也能够存储数据,但在STL中其却不属于容器。
二,栈与队列模拟实现
栈与队列的详细剖析与说明在前面的【1++的数据结构初阶】中已经写过有关文章。若有疑惑可移步至专栏中查看。本篇中进行的实现主要基于适配器的设计模式,因此底层较为简单。
栈的实现
template <class T,class container=std::deque<T>>
class stack
{
public:
void push(const T& val)
{
_con.push_back(val);
}
T& top()
{
return _con.back();
}
void pop()
{
_con.pop_back();
}
size_t size()
{
return _con.size();
}
bool empty()
{
return _con.emnpty();
}
private:
container _con;
};
队列的实现
template<class T,class container=std::deque<T>>
class queue
{
public:
void push(const T& val)
{
_con.push_back(val);
}
void pop()
{
_con.pop_front();
}
T& front()
{
return _con.front();
}
T& back()
{
return _con.back();
}
size_t size()
{
return _con.size();
}
bool empty()
{
return _con.empty();
}
private:
container _con;
};
可能有人会疑惑,模板中的container是什么鬼?

来,让我们看看官方的解释:
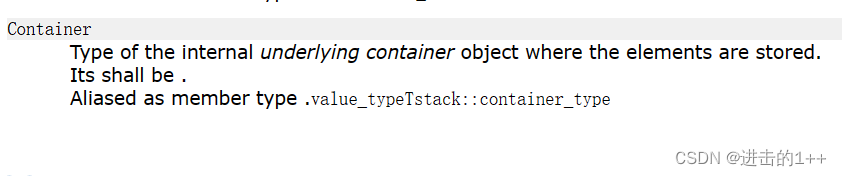
其就是存储元素的内部容器的类型
在直接点就是成员类型。例如:stack中的成员——_con的类型就为deque。
那么问题来了什么又是deque呢?

接下来我们对deque进行一个简单的介绍了。
deque是一种双端队列,其可以在头尾进行插入和删除,并且时间复杂度为O(1)。与vector相比,其可以进行头插与头删;与list相比,其对数据的随机访问的效率高。
是不是对deque的底层实现越发的好奇了。

让我们来解开这层神秘的面纱。
deque的底层空间并不是连续的,而是一个个小块。类似于二维数组一样。
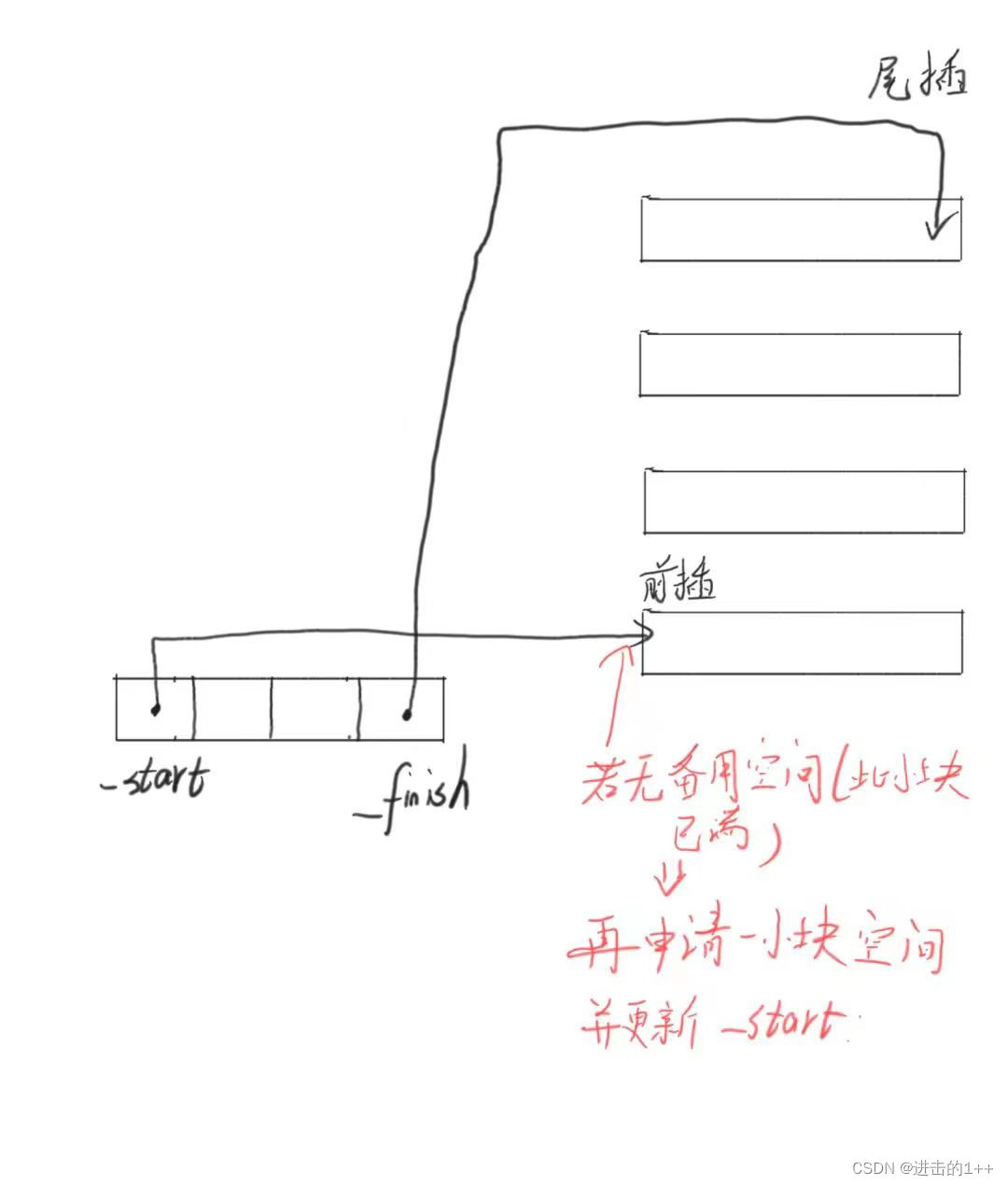
之所以选择deque作为栈和队列的底层默认容器,正是看中了其头尾在进行操作时的高效率。
deque若如此完美,那为什么不大量应用呢?原因在于其也有缺点。
deque在进行遍历时,要经过稍复杂的计算才能够计算出其在哪一块的哪个位置,所以,当数据量大时,其遍历的效率比较低。并且其中间的插入,删除效率也不高。
三,优先级队列
什么是priority_queue(优先级队列)?
它也是一种适配器,其在默认情况下,第一个位置的元素总是最大的。类似于堆。其底层容器的前提是可以通过随机访问迭代器进行随机访问。
priority_queue的实现
template<class T>
class less
{
public:
bool operator()(const T& left, const T& right)const
{
return left < right;
}
};
template<class T>
class greater
{
public:
bool operator()(const T& left, const T& right)const
{
return left > right;
}
};
template<class T,class container=std::vector<T>,class compare=greater<T>>
class priority_queue
{
public:
void adjust_up()
{
size_t child = _con.size() - 1;
size_t parent = (child-1)/2;
while (child > 0)
{
compare com;
if (com(_con[parent],_con[child]))
{
swap(_con[child], _con[parent]);
child = parent;
parent=(child - 1) / 2;
}
else
{
break;
}
}
}
void adjust_down()
{
//默认左孩子为大----大堆前提下
size_t parent = 0;
size_t child = parent* 2+1;
while (child < _con.size())
{
compare com;
if ((child + 1) < _con.size() && com(_con[child], _con[child+1]))
{
child++;
}
if (com(_con[parent], _con[child]))
{
std::swap(_con[parent], _con[child]);
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}
void push(const T& val)
{
//向上调整
_con.push_back(val);
adjust_up();
}
const T& top()const
{
return _con[0];
}
void pop()
{
std::swap(_con.back(), _con[0]);
_con.pop_back();
//向下调整
adjust_down();
}
size_t size()
{
return _con.size();
}
bool empty()
{
return _con.empty();
}
private:
container _con;
};
优先级队列在push建堆时,使用的是向上调整,时间复杂度为O(logN) ,在默认为大堆的情况下,孩子结点于父亲结点比较,若大于父亲结点,则进行交换,直到小于父亲结点或者到达根节点。
在代码中,我们还发现了其比较大小的写法与以往不同。
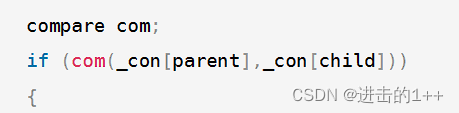
这叫做做仿函数,其与普通函数的调用相差不大,但其本质是类对象调用重载后的(),即operator() 。
四,reverse_iterator
反向适配器其底层为正向迭代器。其也是适配器的一种。
具体实现如下:
template<class Iterator,class Ref,class Ptr>
class reverse_iterator
{
public:
typedef reverse_iterator<Iterator,Ref,Ptr> Riterator;
reverse_iterator(Iterator it)
:cur(it)
{}
Riterator operator++()
{
--cur;
return *this;
}
Riterator operator--()
{
++cur;
return *this;
}
Ref operator*()
{
Iterator tmp = cur;
--tmp;
return *tmp;
}
Ptr operator->()
{
return &(*operator());
}
bool operator!=(const Riterator& it)
{
return cur != it.cur;
}
private:
Iterator cur;
};
reverse_iterator rend()
{
return reverse_iterator(begin());
}
reverse_iterator rbegin()
{
return reverse_iterator(end());
}
反向迭代器与rbegin(),rend() 进行搭配,通过观察我们发现,其rend(),实际返回的是begin(),rbegin()返回的是end()。恰好对称。并且,反向迭代器中的++,实际上为正向迭代器的- -; --则实际上为++。
需要注意的是operator*()的实现。其返回的是当前迭代器指向的元素的下一个元素(右往左数)。这样做的原因是:end()指向的是最后一个元素的下一位置。并且,由于对称的原因,rbegin指向的位置与end相同,因此在返回其元素的时候,就需要返回其下以位置的元素。