1.简述
一、牛顿插值法原理
1.牛顿插值多项式
定义牛顿插值多项式为:
N n ( x ) = a 0 + a 1 ( x − x 0 ) + a 2 ( x − x 0 ) ( x − x 1 ) + ⋯ + a n ( x − x 0 ) ( x − x 1 ) ⋯ ( x − x n − 1 ) N_n\left(x\right)=a_0+a_1\left(x-x_0\right)+a_2\left(x-x_0\right)\left(x-x_1\right)+\cdots+a_n\left(x-x_0\right)\left(x-x_1\right)\cdots\left(x-x_{n-1}\right)
其中a k ( k = 0 , 1 , 2 , ⋯ , n ) a_k\left(k=0,1,2,\cdots,n\right)a k
(k=0,1,2,⋯,n)为待定系数
可见,牛顿插值多项式N ( x ) N\left(x\right)N(x)是插值多项式P ( x ) P\left(x\right)P(x)的另一种表示形式, 与Lagrange多项式相比它不仅克服了“增加一个节点时整个计算工作重新开始”的缺点, 且可以节省乘除法运算次数, 同时在Newton插值多项式中用到差分与差商等概念,又与数值计算的其他方面有密切的关系.
2.差商
2.1 定义
自变量之差与因变量之差之比叫差商
定义: 函数y = f ( x ) y=f\left(x\right)y=f(x)在区间[ x i , x i + 1 ] \left[x_i,x_{i+1}\right][x
上的平均变化率
f [ x i , x i + 1 ] = f ( x i + 1 ) − f ( x i ) x i + 1 − x i f\left[x_i,x_{i+1}\right]=\frac{f\left(x_{i+1}\right)-f\left(x_i\right)}{x_{i+1}-x_i}
2.2 性质
性质1:函数f ( x ) f\left(x\right)f(x)的 n 阶差商f [ x 0 , x 1 , ⋯ , x n ] 可由函数值f ( x 0 ) , f ( x 的线性组合表示, 且
f [ x 0 , x 1 , ⋯ , x n ] = ∑ k = 0 n f ( x k ) ω ′ ( x k ) = ∑ k = 0 n f ( x k ) ( x k − x 0 ) ( x k − x 1 ) ⋯ ( x k − x k − 1 ) ( x − x k + 1 ) ⋯ ( x k − x n ) f\left[x_0,x_1,\cdots,x_n\right]=\sum_{k=0}^n\frac{f\left(x_k\right)}{\omega'\left(x_k\right)}\\=\sum_{k=0}^n\frac{f\left(x_k\right)}{\left(x_k-x_0\right)\left(x_k-x_1\right)\cdots\left(x_k-x_{k-1}\right)\left(x-x_{k+1}\right)\cdots\left(x_k-x_n\right)}
性质2:差商具有对称性,即在k阶差商中f [ x 0 , x 1 , ⋯ , x n ] f\left[x_0,x_1,\cdots,x_n\right]f[x
的次序,其值不变。
例如:
f [ x 0 , x 1 , x 2 ] = f [ x 1 , x 2 , x 0 ] = f [ x 0 , x 2 , x 1 ] = ⋯ f\left[x_0,x_1,x_2\right]=f\left[x_1,x_2,x_0\right]=f\left[x_0,x_2,x_1\right]=\cdots
性质3:k阶差商f [ x 0 , x 1 , ⋯ , x k ] f\left[x_0,x_1,\cdots,x_k\right]f[x
和k阶导数之间有下列关系
f [ x 0 , x 1 , ⋯ , x k ] = f ( k ) ( ξ ) k ! ξ ∈ ( m i n 0 ≤ i ≤ n x i , m a x 0 ≤ i ≤ n x i ) f\left[x_0,x_1,\cdots,x_k\right]=\frac{f^{\left(k\right)}\left(\xi\right)}
将求得系数代入多项式中即可得到n次牛顿插值公式
N n ( x ) = f ( x 0 ) + f [ x 0 , x 1 ] ( x − x 0 ) + ⋯ + f [ x 0 , x 1 , ⋯ , x n ] ( x − x 0 ) ( x − x 1 ) ⋯ ( x − x n ) N_n\left(x\right)=f\left(x_0\right)+f\left[x_0,x_1\right]\left(x-x_0\right)+\cdots+f\left[x_0,x_1,\cdots,x_n\right]\left(x-x_0\right)\left(x-x_1\right)\cdots\left(x-x_n\right)
二、牛顿插值公式matlab代码
友情提示:本人使用的是matlab2019b版本,并且个人很喜欢使用matlab中的实时在线脚本,很少使用脚本来编写程序。实时在线脚本脚本编译环境我个人非常喜欢,所以接下来的代码都是在实时在线脚本中实现。
2.代码
function Newton_main()
clc
x=0:1:10;
y=x./(tan(x)+1);
k=1;
for x0=0:0.01:10;
y0(k)=Newton(x,y,x0);
k=k+1;
end
x0=0:0.01:10;
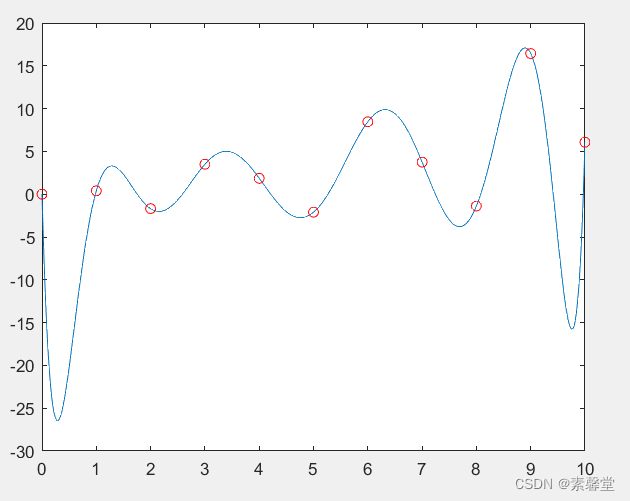
plot(x0,y0)
hold on
scatter(x,y,'ro')
end
function y0=Newton(x,y,x0)
n=length(x);
A=zeros(n);
A(:,1)=y';
for j=2:n
for i=1:(n-j+1)
A(i,j)=(A(i+1,j-1)-A(i,j-1))/(x(i+j-1)-x(i));
end
end
N(1)=A(1,1);
for j=2:n
T=1;
for i=1:j-1
T=T*(x0-x(i));
end
N(j)=A(1,j)*T;
end
y0=sum(N);
end
3.运行结果