【C语言趣味教程】(3) 浮点类型：单精度浮点数 | 双精度浮点型 | IEEE754 标准

   🔗 《C语言趣味教程》👈 猛戳订阅！！！

​—— 热门专栏《维生素C语言》的重制版 ——

• 💭 写在前面：这是一套 C 语言趣味教学专栏，目前正在火热连载中，欢迎猛戳订阅！本专栏保证篇篇精品，继续保持本人一贯的幽默式写作风格，当然，在有趣的同时也同样会保证文章的质量，旨在能够产出 "有趣的干货" ！本系列教程不管是零基础还是有基础的读者都可以阅读，可以先看看目录！ 标题前带星号 (*) 的部分不建议初学者阅读，因为内容难免会超出当前章节的知识点，面向的是对 C 语言有一定基础或已经学过一遍的读者，初学者可自行选择跳过带星号的标题内容，等到后期再回过头来学习。值得一提的是，本专栏 强烈建议使用网页端阅读！ 享受极度舒适的排版！你也可以展开目录，看看有没有你感兴趣的部分！希望需要学 C 语言的朋友可以耐下心来读一读。最后，可以订阅一下专栏防止找不到。

" 有趣的写作风格，还有特制的表情包，而且还干货满满！太下饭了！"

—— 沃兹基硕德

📜 本章目录：

Ⅰ. 浮点类型（Float Point）

0x00 引入：什么是浮点数？

0x01 单精度浮点型：float

0x02 双精度浮点型：double

0x03 浮点数 “精度丢失” 问题

0x04 浮点数类型的表达方式

* 0x05 复数浮点型：complex_float / complex double

Ⅱ. 二进制浮点数算术标准（IEEE754）

0x00 引入：浮点数的存储

0x01 IEEE754 规定

0x02 阅读：雷神之锤 III 源码中的 "平方根倒数速算法"

Ⅲ. 浮点数类型的表达方式（Float Expression）

0x00 引入：浮点数类型的表示

0x01 十进制小数型：x.

0x02 指数型：xEn

Ⅰ. 浮点类型（Float Point）

0x00 引入：什么是浮点数？

在讲解浮点类型前，我们不妨先先来了解一下什么是浮点数，浮点 (float point)：

顾名思义就是 "一个漂浮的点"，其英文 float 也是这个含义（浮动, 漂浮之意）。

因此，浮点数指的是一个数的小数点的位置不是固定的，而是可以浮动的。

浮点数在数学中的定义：浮点数是属于有理数中某个特定子集的数的数字表示。

C 语言的浮点型是用来存放小数类型的数字的，可分为 单精度 和 双精度，我们稍后会作讲解。

" 程序员不得不知道的标准，IEEE754 标准！ "

电气电子工程师学会 (IEEE) 颁布过一个浮点数标准，全称 IEEE 二进制浮点算数标准。

简称 IEEE754，是被绝大部分 CPU 和浮点运算器所采用的一套浮点数标准。

0x01 单精度浮点型：float

我们可以用 float 类型来表示小数，称为 单精度浮点型 (single floating-point) 。

float 变量名 = 值;

float 的精度为 6~7 位小数，float 类型占 4 个字节。

我们来使用 float 定义一些变量：

float height = 170.00;
float weight = 50.5;
float pi = 3.14;
float zero = 0.0;

我们可以使用 float 专属的格式化字符 %f 来打印浮点类型变量。

💬 代码演示：打印浮点数

#include <stdio.h>

int main(void)
{
    float pi = 3.14;
    printf("%f", pi);

    return 0;
}

🚩 运行结果：3.140000

此时我们发现结果为 3.140000，而不是 3.14，因为把精度全部都打出来了。

我们可以用 %.Xf 来控制保留小数点位数，其中 X 是几就保留几位。

这里我们想保留两位，所以 %.2f 即可：

#include <stdio.h>

int main(void)
{
    float pi = 3.14;
    printf("%.2f", pi);

    return 0;
}

🚩 运行结果：3.14

0x02 双精度浮点型：double

刚才介绍了单精度浮点型 float，表示的数需要的精度较低，就可以用 float 来定义。

如果表示的数要求的精度较高，我们就可以使用 double 类型来定义。

double 即 双精度浮点型 (double floating-point)，double 类型的精度比 float 类型要高得多。

double 变量名 = 值;

double 类型的精度为 15~16 位小数，相应的占的字节数也更多，double 类型占 8 个字节。

我们可以使用 double 专属的格式化字符 %lf 来打印 double 类型的变量：

#include <stdio.h>

int main(void)
{
    double pi = 3.141592;
    printf("%lf\n", pi);

    return 0;
}

🚩 运行结果：3.141592

0x03 浮点数 “精度丢失” 问题

浮点数精度丢失是指在使用浮点数进行数值计算时，由于浮点数的二进制表示方式的特殊性，导致某些精确的数值无法准确表示，从而引起计算结果的误差。

浮点数在计算机中使用二进制表示，通常采用IEEE 754标准来表示单精度浮点数（32位）和双精度浮点数（64位）。无论是单精度还是双精度浮点数，都有固定的位数来表示整数部分和小数部分，这就导致了有些十进制数无法用有限的二进制位数准确表示。

例如，考虑一个简单的示例，计算 0.1 + 0.2。在十进制中，这个结果是 0.3，但是在浮点数表示中，由于 0.1 和 0.2 的二进制表示是无限循环的，所以它们的精确表示会受到限制。因此，计算机在进行浮点数计算时可能得到一个近似的结果，比如 0.30000000000000004。

浮点数精度丢失问题还可能在连续的计算中累积误差，导致最终结果的精度下降。这是由于浮点数的表示范围是有限的，无法表示所有的实数，因此在计算过程中可能会出现舍入误差和截断误差。

* 0x05 复数浮点型：complex_float / complex double

C99 标准新增了复数类型 _Complex 和虚部类型 _lmaginary。

定义复数浮点型前需引入头文件 complex.h，定义格式如下：

#include <complex.h>

float complex a = 3.0 + 4.0 * I;
double complex b = 4.0 - 5.0 * I;

其中  表示虚数单位，complex 可以根据我们需要的精度定义。

C 语言不仅支持复数浮点型的加减乘除操作，还支持求模、求共轭等操作。

💬 代码演示：完成一些复数操作

#include <stdio.h>
#include <complex.h>

int main(void) 
{
    // 定义两个复数
    double complex num1 = 2.5 + 3.7 * I;
    double complex num2 = 1.8 - 2.3 * I;

    // 加法
    double complex sum = num1 + num2;
    printf("%.2f + %.2fi\n", creal(sum), cimag(sum));

    // 减法
    double complex diff = num1 - num2;
    printf("%.2f + %.2fi\n", creal(diff), cimag(diff));

    // 乘法
    double complex product = num1 * num2;
    printf("%.2f + %.2fi\n", creal(product), cimag(product));

    // 除法
    double complex quotient = num1 / num2;
    printf("%.2f + %.2fi\n", creal(quotient), cimag(quotient));

    // 求模
    double modulus = cabs(num1);
    printf("%.2f\n", modulus);

    // 求共轭
    double complex conjugate = conj(num1);
    printf("%.2f + %.2fi\n", creal(conjugate), cimag(conjugate));

    return 0;
}

🚩 运行结果如下：

4.30 + 1.40i
0.70 + 6.00i
13.01 + 0.91i
-0.47 + 1.45i
4.47
2.50 + -3.70i

Ⅱ. 二进制浮点数算术标准（IEEE754）

0x00 引入：浮点数的存储

在讲解之前我们先来试着观察下列程序的输出结果：

int main(void)
{
	int n = 9;

	float* pFloat = (float*)&n;
	printf("n的值为: %d\n", n);
	printf("*pFloat的值为 %f\n", *pFloat);

	*pFloat = 9.0;
	printf("num的值为: %d\n", n);
	printf("*pFloat的值为: %f\n", *pFloat);

	return 0;
}

🚩 运行结果如下：

​

❓ 思考：num 和 *pFloat 在内存中明明是同一个数，为什么浮点数和整数的结果会差这么大？

​

由此可以看出，浮点数和整数在内存中的存储方式一定是有区别的。

那么具体是什么样的区别？着我们就不得不去介绍开篇提到的 IEEE754 规定了。

0x01 IEEE754 规定

IEEE754 规定，任意一个二进制浮点数  可以表示成以下形式：

• 其中，  表示符号位，当  时  为正数，当  时  为负数
•  表示有效数字，
•  表示指数位

💭 举个例子：浮点数 5.5

转换为二进制：

🔺 IEEE 754 规定：

对于 32 位浮点数，最高的 1 位是符号位 ，接着 8 位是指数 ，剩下的 23 位是有效数字 ：

​

对于 64 位浮点数，最高的 1 位是符号位 ，接着 11 位是指数 ，剩下的 52 位是有效数字 ：

​

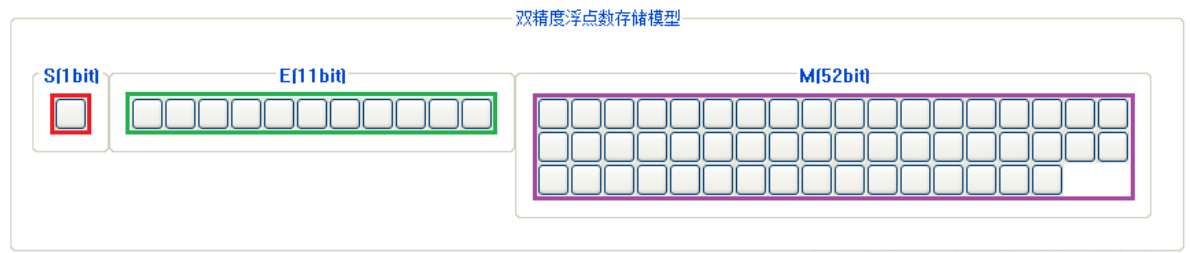
IEEE 754 对有效数字M和指数E，还有一些特别规定！

前面说过， ，也就是说， 可以写成 1.xxxxxx 的形 式，其中 xxxxxx 表示小数部分。IEEE 754 规定，在计算机内部保存  时，默认这个数的第一位总是 1，因此可以被舍去，只保存后面的 xxxxxx 部分。 比如保存 1.01 的时候，只保存 01，等到读取的时候，再把第一位的1加上去。这样做的目的，是节省1位有效数字。以 32 位浮点数为例，留给 M 只有 23 位，将第一位的 1 舍去以后，等于可以保存 24 位有效数字。

至于指数 E，情况就比较复杂。 首先，E为一个无符号整数（unsigned int） 这意味着，如果E为8位，它的取值范围为0~255；如果E为11位，它的 取值范围为0~2047。但是，我们知道，科学计数法中的E是可以出现负数的，所以IEEE 754规定，存入内存时E的真 实值必须再加上一个中间数，对于8位的E，这个中间数是127；对于11位的E，这个中间数是1023。比如，2^10的E 是10，所以保存成32位浮点数时，必须保存成10+127=137，即10001001。

​

然后，指数E从内存中取出还可以再分成三种情况：

E不全为0或不全为1

这时，浮点数就采用下面的规则表示，即指数E的计算值减去127（或1023），得到真实值，再将有效数字M前 加上第一位的1。 比如： 0.5（1/2）的二进制形式为0.1，由于规定正数部分必须为1，即将小数点右移1位， 则为1.0*2^(-1)，其阶码为-1+127=126，表示为01111110，而尾数1.0去掉整数部分为0，补齐0到23位 00000000000000000000000，则其二进制表示形式为

0 01111110 00000000000000000000000

E全为0

这时，浮点数的指数E等于1-127（或者1-1023）即为真实值， 有效数字M不再加上第一位的1，而是还原为 0.xxxxxx的小数。这样做是为了表示±0，以及接近于0的很小的数字。

E全为1

这时，如果有效数字M全为0，表示±无穷大（正负取决于符号位s）；

此时，再看前面的例子，问题就很好理解了： 

​

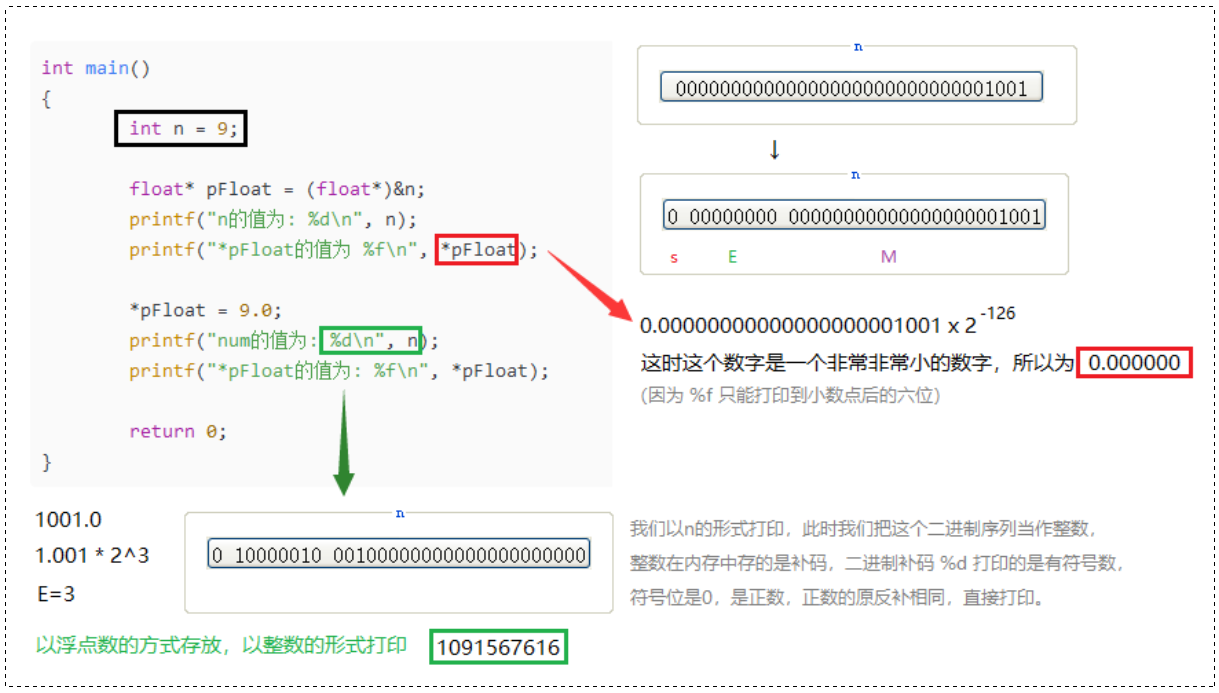
🔺 浮点数在内存中的分布：符号位 + 指数位 + 尾部部分

0x02 阅读：雷神之锤 III 源码中的 "平方根倒数速算法"

" evil floating point bit level hacking, what the fuck? "

—— Quake III

  （雷神之锤 III 游戏截图）

雷神之锤III 是由 id Software 采用 id Tech3 引擎制作的多人连线 FPS 游戏，1999年12月发行。玩家或独立或组队在地图中厮杀，死亡后数秒即在地图某处重生。当某位或某队玩家达到胜利条件或者游戏持续一定时间后即宣告一个回合结束。胜利条件取决于选择的游戏模式。

雷神之锤 III 的源码中有一段震惊四座的代码：

float Q_rsqrt( float number )
{
  long i;
  float x2, y;
  const float threehalfs = 1.5f;
  x2 = number * 0.5f;
  y  = number;
  i  = * ( long * ) &y;  // evil floating point bit level hacking
  i  = 0x5f3759df - ( i >> 1 ); // what the fuck?
  y  = * ( float * ) &i;
  y  = y * ( threehalfs - ( x2 * y * y ) ); // 1st iteration
  // y  = y * ( threehalfs - ( x2 * y * y ) ); // 2nd iteration, this can be removed
  return y;
}

这是一个快速逆平方根的算法，求一个数的平方根的倒数。

常规的方法是调用 math 库里的 sqrt 求一个数的平方根，求平方根的倒数只需要：

float y = 1 / sqrt(x);

而作者实现的算法要比这种常规方法快得多，在计算浮点数的平方根倒数的同一精度的近似值时，此算法比直接使用浮点数除法要快四倍。其中还有一串神秘数字：0x5f3759df，更是给这段代码留下了最具神秘、浓墨重彩的一笔。还对它进行了位移，机器码位移，WTF？

该算法被称为 平方根倒数速算法 (Fast Inverse Square Root)，对代码原理感兴趣的读者可以阅读下面这篇 wiki，有对该算法详细的讲解。

🔗 链接：Fast inverse square root

 Fast Inverse Square Root 的历史

Quake III Arena 是一款第一人称射击游戏，由id Software于 1999 年发布，并使用了该算法。Brian Hook 可能将 3dfx 的算法引入了 id Software。2000 年中国开发者论坛 CSDN 上出现了对该代码的讨论， 以及2002 年和 2003 年Usenet和 gamedev.net 论坛广泛传播了该代码。人们猜测谁编写了该算法和常数是如何导出的，有人猜测是约翰·卡马克。Quake III的完整源代码在QuakeCon 2005上发布，但没有提供答案。作者身份问题已于 2006 年得到解答。2007 年，该算法在一些使用现场可编程门阵列(FPGA)的专用硬件顶点着色器中实现。

Ⅲ. 浮点数类型的表达方式（Float Expression）

0x00 引入：浮点数类型的表示

符合 C 标准法的浮点数有两种表达形式，分别是 十进制小数型 和 指数型。

0x01 十进制小数型：x.

十进制小数型：由数字和小数点组成：

💭 举个例子：下面这三种方式都是合法的：

123.     ✅
1.23     ✅
.123     ✅

小数点前后的数是可以省略的，小数点不可省略，省略了就不是浮点数了。

💬 代码演示：

#include <stdio.h>

int main(void)
{
    float a = 1.0;
    printf("%f\n", a);

    float b = 1.;
    printf("%f\n", b);

    float c = .1;
    printf("%f\n", c);

    return 0;
}

🚩 运行结果如下：

0x02 指数型：xEn

指数型：由字母  和数字组成（这里  也可以是小写）：

其中  必须是一个十进制小数型，和上面的规则一样，点的位置都是合法的。

 必须是整型常量，且不能是表达式，并且  和  都不能省略。

💭 举个例子：只有前面 4 个是合法的

1.23e5         ✅ 
12345e6        ✅
3.14E7         ✅
.2e3           ✅
.e3            ❌ e 前面没有数
e3             ❌ e 前面没有数
3.14e          ❌ e 后面没有数
3.e6.2         ❌ e 后面必须是整数
5.0e(1+4)      ❌ 不能为表达式

指数型的表达方式非常苛刻，这里有一个口诀方便大家记忆：

" E 前 E 后必有数，E 后必定为整数。"

💬 代码演示：

#include <stdio.h>

int main(void)
{
    float a = .23e4;
    printf("%f\n", a);

    float b = 1234e6;
    printf("%f\n", b);

    float c = 3.14E7;
    printf("%f\n", c);

    return 0;
}

🚩 运行结果如下：

​

📌 [ 笔者 ]   王亦优 | 雷向明
📃 [ 更新 ]   2023.7.17 | 2023.7.20（recently）
❌ [ 勘误 ]   /* 暂无 */
📜 [ 声明 ]   由于作者水平有限，本文有错误和不准确之处在所难免，
              本人也很想知道这些错误，恳望读者批评指正！