介绍
最近我们被客户要求撰写关于向量自回归的研究报告,包括一些图形和统计输出。向量自回归(VAR)模型的一般缺点是,估计系数的数量与滞后的数量成比例地增加。因此,随着滞后次数的增加,每个参数可用的信息较少。在贝叶斯VAR文献中,减轻这种所谓的维数诅咒的一种方法是随机搜索变量选择(SSVS),由George等人提出(2008)。SSVS的基本思想是将通常使用的先验方差分配给应包含在模型中的参数,将不相关参数的先验方差接近零。这样,通常就可以估算出相关参数,并且无关变量的后验值接近于零,因此它们对预测和冲激响应没有显着影响。这是通过在模型之前添加层次结构来实现的,其中在采样算法的每个步骤中评估变量的相关性。
视频:线性回归中的贝叶斯推断与R语言预测工人工资数据案例
贝叶斯推断线性回归与R语言预测工人工资数据
,时长09:58
视频:向量自回归VAR数学原理及R软件经济数据脉冲响应分析实例
【视频】向量自回归VAR数学原理及R语言软件经济数据脉冲响应分析实例
,时长12:01
这篇文章介绍了使用SSVS估计贝叶斯向量自回归(BVAR)模型。它使用Lütkepohl(2007)的数据集E1,其中包含有关1960Q1至1982Q4德国固定投资,可支配收入和消费支出的数据。加载数据并生成数据:
# 加载和转换数据
e1 <- diff(log(e1))
# 生成VAR
data <- gen_var(e1, p = 4, deterministic = "const")
# 获取数据矩阵
y <- data$Y[, 1:71]
x <- data$Z[, 1:71]估算值
根据George等人所述的半自动方法来设置参数的先验方差(2008)。对于所有变量,先验包含概率设置为0.5。误差方差-协方差矩阵的先验信息不足。
# 重置随机数提高可重复性
set.seed(1234567)
t <- ncol(y) # 观察数
k <- nrow(y) # 内生变量数
m <- k * nrow(x) # 估计系数数
# 系数先验
a_mu_prior <- matrix(0, m) # 先验均值的向量
# SSVS先验(半自动方法)
ols <- tcrossprod(y, x) %*% solve(tcrossprod(x)) # OLS估计
sigma_ols <- tcrossprod(y - ols %*% x) / (t - nrow(x)) # OLS误差协方差矩阵
cov_ols <- kronecker(solve(tcrossprod(x)), sigma_ols)
se_ols <- matrix(sqrt(diag(cov_ols))) # OLS标准误
# 先验参数
prob_prior <- matrix(0.5, m)
# 方差-协方差矩阵
u_sigma_df_prior <- 0 # 方差-协方差矩阵
u_sigma_scale_prior <- diag(0, k) # 先验协方差矩阵
u_sigma_df_post <- t + u_sigma_df_prior # 后验自由度初始参数值设置为零,这意味着在Gibbs采样器的第一步中应相对自由地估算所有参数。
可以直接将SSVS添加到VAR模型的标准Gibbs采样器算法中。在此示例中,常数项从SSVS中排除,这可以通过指定来实现include = 1:36。具有SSVS的Gibbs采样器的输出可以用通常的方式进一步分析。因此,可以通过计算参数的绘制方式获得点估计:
## invest income cons
## invest.1 -0.102 0.011 -0.002
## income.1 0.044 -0.031 0.168
## cons.1 0.074 0.140 -0.287
## invest.2 -0.013 0.002 0.004
## income.2 0.015 0.004 0.315
## cons.2 0.027 -0.001 0.006
## invest.3 0.033 0.000 0.000
## income.3 -0.008 0.021 0.013
## cons.3 -0.043 0.007 0.019
## invest.4 0.250 0.001 -0.005
## income.4 -0.064 -0.010 0.025
## cons.4 -0.023 0.001 0.000
## const 0.014 0.017 0.014
还可以通过计算变量的均值来获得每个变量的后验概率。从下面的输出中可以看出,在VAR(4)模型中似乎只有几个变量是相关的。常数项的概率为100%,因为它们已从SSVS中排除。
## invest income cons
## invest.1 0.43 0.23 0.10
## income.1 0.10 0.18 0.67
## cons.1 0.11 0.40 0.77
## invest.2 0.11 0.09 0.14
## income.2 0.08 0.07 0.98
## cons.2 0.07 0.06 0.08
## invest.3 0.19 0.07 0.06
## income.3 0.06 0.13 0.10
## cons.3 0.09 0.07 0.12
## invest.4 0.78 0.09 0.16
## income.4 0.13 0.09 0.18
## cons.4 0.09 0.07 0.06
## const 1.00 1.00 1.00
给定这些值,研究人员可以按照常规方式进行操作,并根据Gibbs采样器的输出获得预测和脉冲响应。这种方法的优势在于它不仅考虑了参数不确定性,而且还考虑了模型不确定性。这可以通过系数的直方图来说明,该直方图描述了收入的第一个滞后项与消费当前值之间的关系。
hist(draws_a[6,], 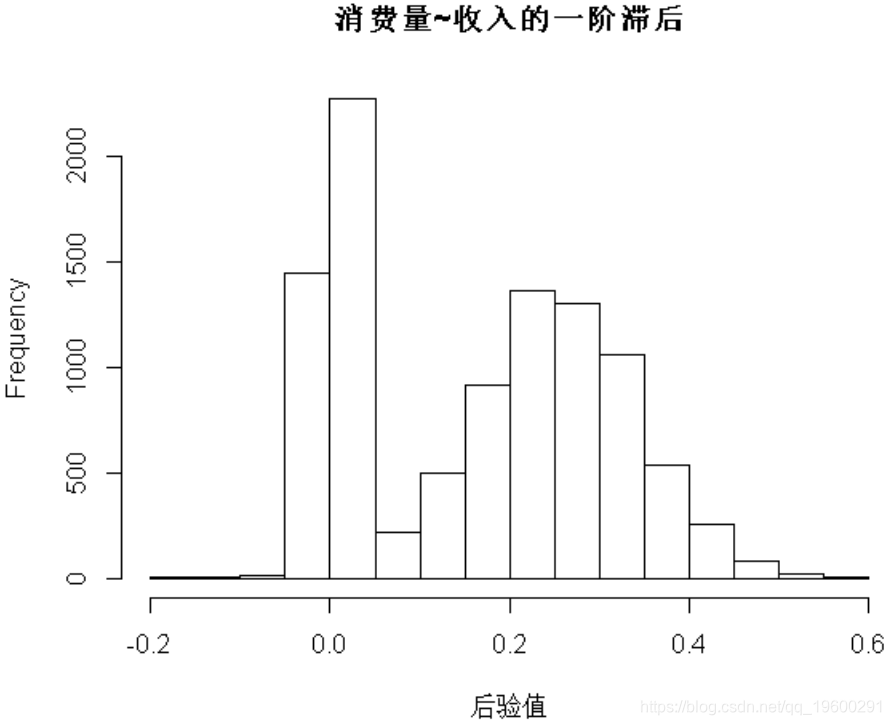
通过两个峰描述模型不确定性,并通过右峰在它们周围的分布来描述参数不确定性。
但是,如果研究人员不希望使用模型,变量的相关性可能会从采样算法的一个步骤更改为另一个步骤,那么另一种方法将是仅使用高概率的模型。这可以通过进一步的模拟来完成,在该模拟中,对于不相关的变量使用非常严格的先验,而对于相关参数则使用没有信息的先验。
后方抽取的均值类似于Lütkepohl(2007,5.2.10节)中的OLS估计值:
## invest income cons
## invest.1 -0.219 0.001 -0.001
## income.1 0.000 0.000 0.262
## cons.1 0.000 0.238 -0.334
## invest.2 0.000 0.000 0.001
## income.2 0.000 0.000 0.329
## cons.2 0.000 0.000 0.000
## invest.3 0.000 0.000 0.000
## income.3 0.000 0.000 0.000
## cons.3 0.000 0.000 0.000
## invest.4 0.328 0.000 -0.001
## income.4 0.000 0.000 0.000
## cons.4 0.000 0.000 0.000
## const 0.015 0.015 0.014
评价
bvar功能可用于将Gibbs采样器的相关输出收集到标准化对象中,例如predict获得预测或irf进行脉冲响应分析。
hin(bvar_est, thin = 5)
预测
可以使用函数获得置信区间的预测predict。
plot(bvar_pred)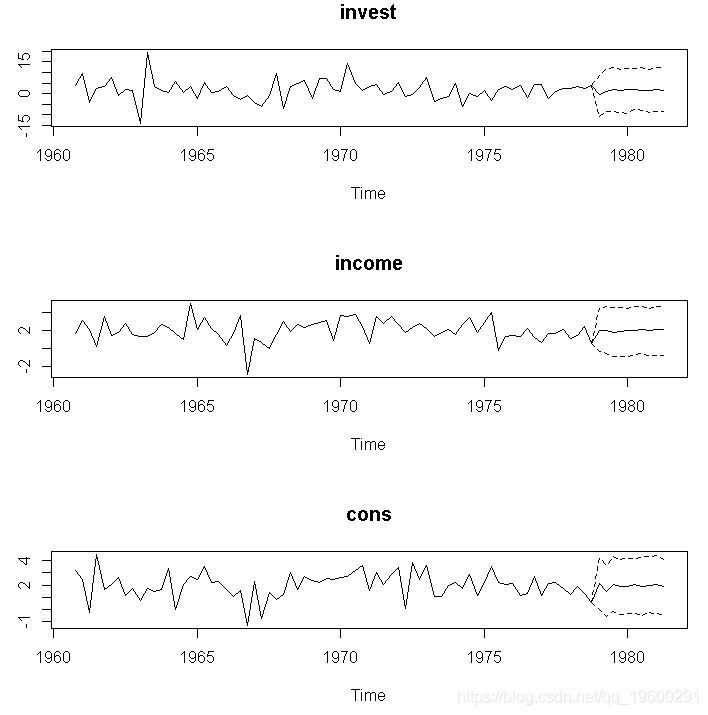
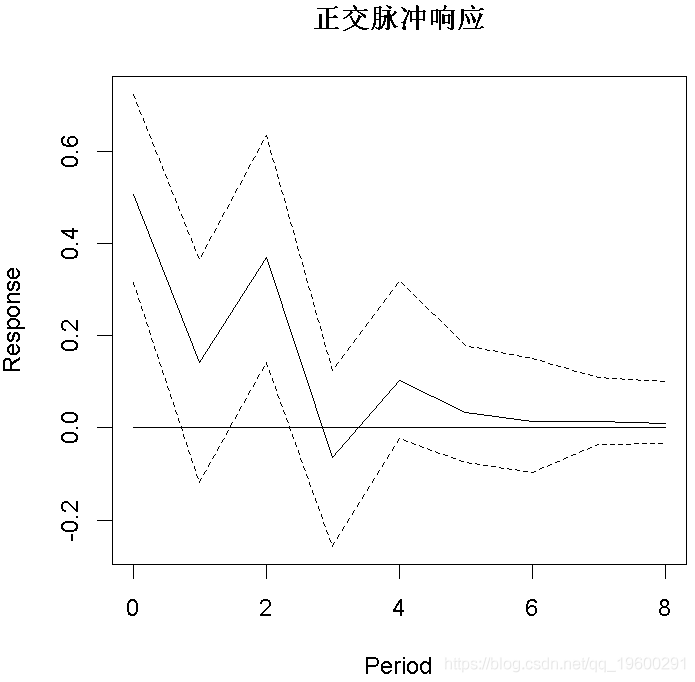
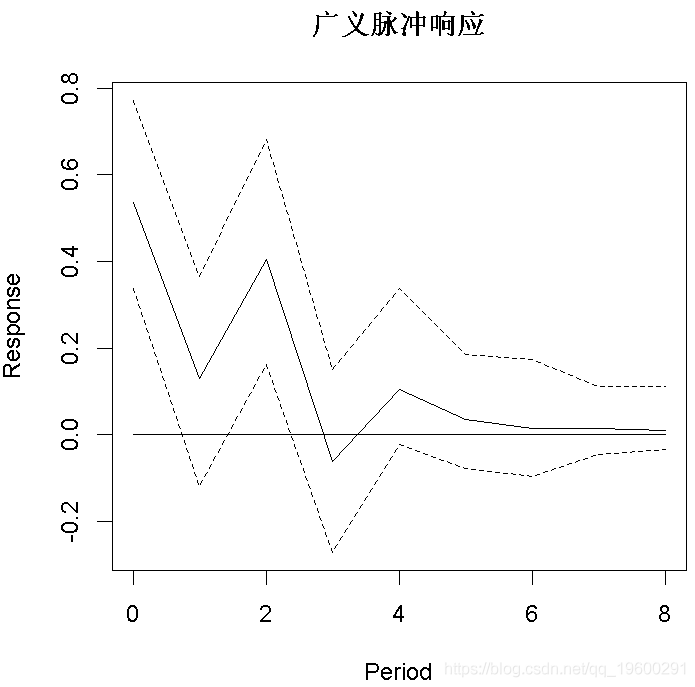
脉冲响应分析
plot(OIR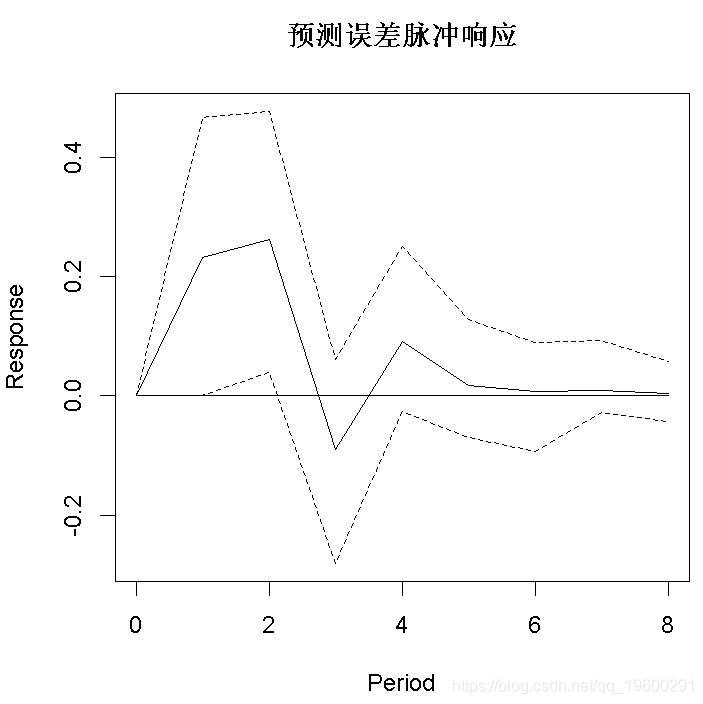






![[趣味][人工智能生成文字]chatGPT使用教程](https://img-blog.csdnimg.cn/8fa22f507b9e4bfca523033add76fe16.png)