1. 解决了什么问题?
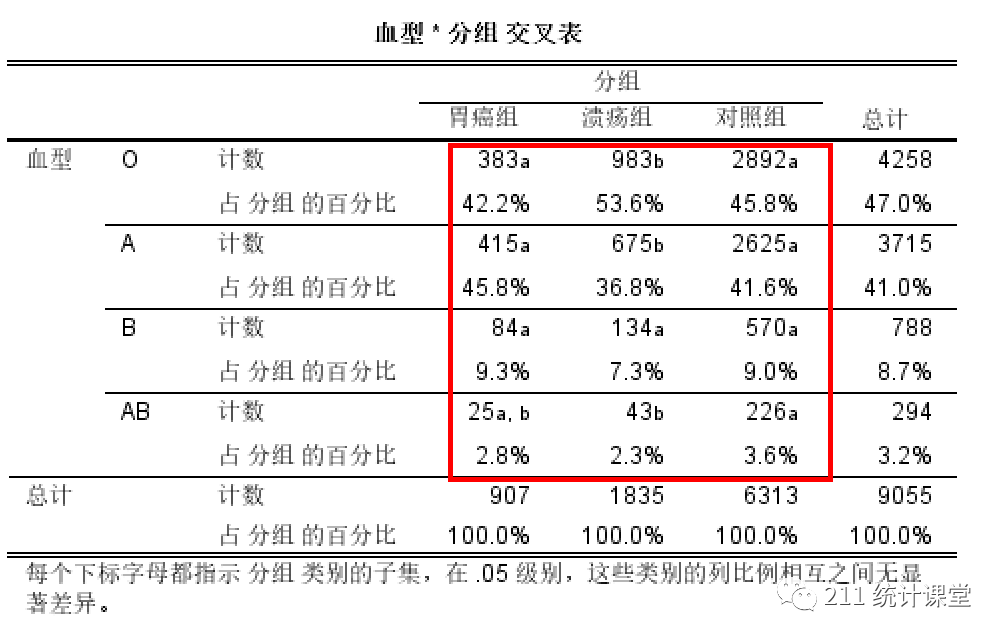
目标检测取得了显著成绩,但是检测不同尺度的目标仍然是一个挑战。金字塔或多层级特征是解决目标检测中尺度变化的常用手段。但对于单阶段目标检测器而言,各特征尺度之间不一致性制约了算法的表现。与图像金字塔相比,特征金字塔在各尺度间是不一致的,要用到启发式的特征选取策略:大目标通常与高层级特征图有关,而小目标则和低层级特征图有关系。当某层级的特征图上的目标被分配为正样本,其它层级特征图的相应区域就会被看作为背景。这种不一致性会对梯度计算造成影响,使特征金字塔的效力降低。
2. 提出了什么方法?
ASFF 解决单阶段目标检测器中特征金字塔存在的不一致性。ASFF 使网络学习过滤掉其它层级有冲突的信息,只保留有用的信息。对于某层级特征,首先整合其它层级的特征,缩放到相同大小的分辨率,然后进行训练,找到最佳的融合方案。在每个空间位置上,自适应地融合不同层级的特征。一些特征因为它们携带了冲突信息,就会被滤掉;另一些特征因为信息更具判别度则发挥更加重要的作用。
2.1 Baseline
采用了 YOLOv3 框架,包含了 DarkNet-53 主干网络,以及三个层级的 FPN。采用了诸多 tricks 来提升性能,如 mixup 数据增强、余弦退火学习率机制,以及 Sync-BN。此外,使用了一个 anchor-free 分支,与 anchor-based 分支协同训练。在原来的 smooth L1 损失基础上,增加了 IOU 损失函数,更好地进行边框回归。
2.2 ASFF
之前的方法使用 element-wise 求和或 concat 操作来整合多层级特征,本方法则自适应地学习各尺度特征图在融合时的空间权重。包括了两个步骤:恒等缩放、自适应融合。

2.2.1 特征缩放
将第 l ∈ { 1 , 2 , 3 } l\in\lbrace1,2,3\rbrace l∈{1,2,3}层级的特征记做 x l \mathbf{x}^l xl。对于层级 l l l,将其它层级 n ( n ≠ l ) n(n\neq l) n(n=l)的特征 x n \mathbf{x}^n xn缩放至与 x l \mathbf{x}^l xl相同的大小。因为 YOLOv3 三个层级的分辨率和通道数都不相同,因此要修改每个尺度的上采样和下采样策略。对于上采样,首先用一个 1 × 1 1\times 1 1×1卷积来压缩特征通道数,与层级 l l l通道数相等,然后通过插值增大分辨率。对于 1 / 2 1/2 1/2比率的下采样,使用步长为 2 2 2的 3 × 3 3\times 3 3×3卷积层,同时调整通道数和分辨率(对于尺度比率为 1 / 4 1/4 1/4的情况,在步长为 2 2 2的卷积层前增加一个步长为 2 2 2的最大池化层)。
2.2.2 自适应融合
在由层级
n
n
n缩放到
l
l
l的特征图上,位置
(
i
,
j
)
(i,j)
(i,j)的特征向量记做
x
i
j
n
→
l
\mathbf{x}_{ij}^{n\rightarrow l}
xijn→l。融合相应层级
l
l
l的特征:
y
i
j
l
=
α
i
j
l
⋅
x
i
j
1
→
l
+
β
i
j
l
⋅
x
i
j
2
→
l
+
γ
i
j
l
⋅
x
i
j
3
→
l
\mathbf{y}_{ij}^l = \alpha_{ij}^l \cdot \mathbf{x}_{ij}^{1\rightarrow l} + \beta_{ij}^l \cdot \mathbf{x}_{ij}^{2\rightarrow l} + \gamma_{ij}^l \cdot \mathbf{x}_{ij}^{3\rightarrow l}
yijl=αijl⋅xij1→l+βijl⋅xij2→l+γijl⋅xij3→l
y
i
j
l
\mathbf{y}_{ij}^l
yijl是输出特征图
y
l
\mathbf{y}^l
yl上第
(
i
,
j
)
(i,j)
(i,j)个向量。
α
i
j
l
,
β
i
j
l
,
γ
i
j
l
\alpha_{ij}^l,\beta_{ij}^l,\gamma_{ij}^l
αijl,βijl,γijl是特征图上三个层级相对于层级
l
l
l的空间权重,由网络自适应地学习得到。
α
i
j
l
,
β
i
j
l
,
γ
i
j
l
\alpha_{ij}^l,\beta_{ij}^l,\gamma_{ij}^l
αijl,βijl,γijl可以是简单的标量变量,在所有通道之间共享。要求
α
i
j
l
+
β
i
j
l
+
γ
i
j
l
=
1
\alpha_{ij}^l+\beta_{ij}^l+\gamma_{ij}^l=1
αijl+βijl+γijl=1,
α
i
j
l
,
β
i
j
l
,
γ
i
j
l
∈
[
0
,
1
]
\alpha_{ij}^l,\beta_{ij}^l,\gamma_{ij}^l\in \left[0,1\right]
αijl,βijl,γijl∈[0,1],
α
i
j
l
=
e
λ
α
i
j
l
e
λ
α
i
j
l
+
e
λ
β
i
j
l
+
e
λ
γ
i
j
l
\alpha_{ij}^l=\frac{e^{\lambda_{\alpha_{ij}}^l}}{e^{\lambda_{\alpha_{ij}}^l}+e^{\lambda_{\beta_{ij}}^l}+e^{\lambda_{\gamma_{ij}}^l}}
αijl=eλαijl+eλβijl+eλγijleλαijl
这里 α i j l , β i j l , γ i j l \alpha_{ij}^l,\beta_{ij}^l,\gamma_{ij}^l αijl,βijl,γijl用 softmax 函数计算, λ α i j l , λ β i j l , λ γ i j l \lambda_{\alpha_{ij}}^l,\lambda_{\beta_{ij}}^l,\lambda_{\gamma_{ij}}^l λαijl,λβijl,λγijl是控制参数。使用 1 × 1 1\times 1 1×1卷积层分别从 x 1 → l , x 2 → l , x 3 → l \mathbf{x}^{1\rightarrow l},\mathbf{x}^{2\rightarrow l},\mathbf{x}^{3\rightarrow l} x1→l,x2→l,x3→l计算权重标量图 λ α i j l , λ β i j l , λ γ i j l \lambda_{\alpha_{ij}}^l,\lambda_{\beta_{ij}}^l,\lambda_{\gamma_{ij}}^l λαijl,λβijl,λγijl。因而可用反向传播学习。于是,各尺度层级的特征都可自适应地融合起来。然后用 { y 1 , y 2 , y 3 } \lbrace\mathbf{y}^1,\mathbf{y}^2,\mathbf{y}^3\rbrace {y1,y2,y3}用于 YOLOv3 后续的检测。











![[高通平台][WLAN] IEEE802.11mc 介绍](https://img-blog.csdnimg.cn/4679ee740569443f9ef1e0403ba584a6.png)