Problem Statement

There are N sports players.

Among them, there are M incompatible pairs. The i-th incompatible pair (1≤i≤M) is the Ai​-th and Bi​-th players.

You will divide the players into T teams. Every player must belong to exactly one team, and every team must have one or more players. Additionally, for each i=1,2,…,M, the Ai​-th and Bi​-th players must not belong to the same team.

Find the number of ways to satisfy these conditions. Here, two divisions are considered different when there are two players who belong to the same team in one division and different teams in the other.

Constraints

• 1≤T≤N≤10
• 0≤M≤N*(N−1)/2​
• 1≤Ai​<Bi​≤N (1≤i≤M)
• (Ai​,Bi​)!=(Aj​,Bj​) (1≤i<j≤M)
• All input values are integers.

Input

The input is given from Standard Input in the following format:

N T M
A1 B1
A2 B2
A3 B3
...
Am Bm

Output

Print the answer in a single line.

 Sample Input 1

5 2 2
1 3
3 4

Sample Output 1

4

No other division satisfies them, so print 4. 

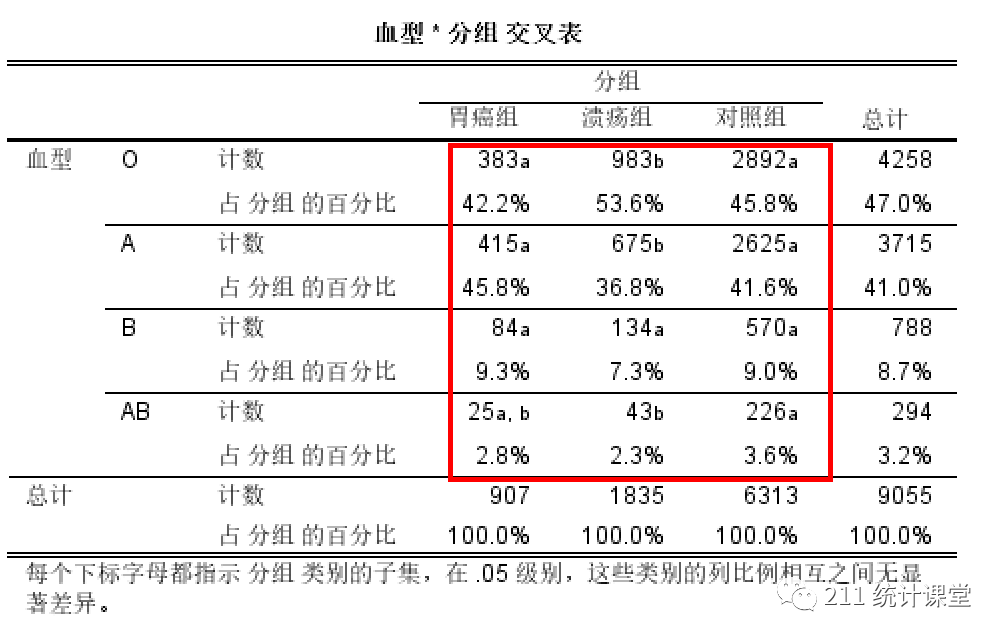
题意：N个人分到T个队伍，M个互斥关系，问有多少种分配方案。

#include <bits/stdc++.h>
using namespace std;
const int N=55;
int n,t,m,a[N],b[N],team[N],ans;
void dfs(int x,int cnt)
{
    if(x==n+1)
    {
        if(cnt!=t) return;
        for(int i=1;i<=m;i++)
        {
            if(team[a[i]]==team[b[i]]) return;
        }
        ans++;
        return;
    }
    for(int i=1;i<=cnt;i++)//安排进1-cnt队伍中
    {
        team[x]=i;
        dfs(x+1,cnt);
        team[x]=0;
    }
    if(cnt+1>t) return;
    team[x]=cnt+1;//新开辟一个队伍
    dfs(x+1,cnt+1);
    team[x]=0;
}
void solve()
{
    scanf("%d%d%d",&n,&t,&m);
    for(int i=1;i<=m;i++) scanf("%d%d",&a[i],&b[i]);
    dfs(1,0);
    printf("%d\n",ans);
}
int main()
{
    int t=1;
    while(t--) solve();
    return 0;
}