写在前面：
首先感谢兄弟们的订阅，让我有创作的动力，在创作过程我会尽最大能力，保证作品的质量，如果有问题，可以私信我，让我们携手共进，共创辉煌。

路虽远，行则将至；事虽难，做则必成。只要有愚公移山的志气、滴水穿石的毅力，脚踏实地，埋头苦干，积跬步以至千里，就一定能够把宏伟目标变为美好现实。

之前我对模型参数寻优喜欢使用网格搜索方法，后来发现大家都喜欢使用“花里胡哨”高大上的启发式算法进行参数寻优，最近也开始接触参数优化方法，见到过：蚁群算法、灰狼算法、秃鹰算法、布谷鸟算法、鱼群算法、蚁群优化、猴群算法，看到这些以动物命名的算法，我人都懵逼了。
在这里插入图片描述
这些算法听起来非常的接地气，实际上也确实很接地气，真是听君一席话，胜似一席话，废话文学在当前社会被发挥的淋漓尽致。言归正传，这些算法，都是学者通过观察动物们的行为得到的灵感，从而设计出来的精彩的算法。以动物命名的算法可远不止上面提到这些，比如还有蜂群算法、狼群算法、蝙蝠算法，萤火虫算法，白鲸算法等，而这些都可以统称为启发式算法。

来看一下启发式算法的定义，摘自百度百科：启发式算法（heuristic algorithm)是相对于最优化算法提出的。一个问题的最优算法求得该问题每个实例的最优解。启发式算法可以这样定义：一个基于直观或经验构造的算法，在可接受的花费（指计算时间和空间）下给出待解决组合优化问题每一个实例的一个可行解，该可行解与最优解的偏离程度一般不能被预计。现阶段，启发式算法以仿自然体算法为主，主要有蚁群算法、模拟退火法、神经网络等。

今天，给大家介绍的一种启发式算法——灰狼优化算法（Grey Wolf Optimizer，GWO）是由自然界中灰狼群体的社会等级机制和捕猎行为而衍生出来的一种群体优化智能算法，目前已成功运用到生产调度、参数优化等领域中。

1.灰狼群的等级制度

灰狼隶属于群居生活的犬科动物，是食物链的顶级掠食者，它们严格遵守着一个社会支配等级关系。如图所示：

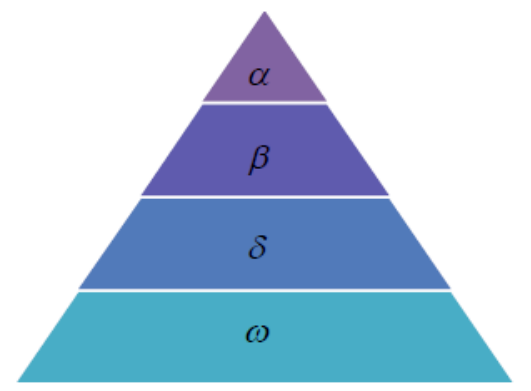
在这里插入图片描述
灰狼群通常分为4个等级：
处于第一等级的灰狼是领头狼，用α表示，它们主要负责各类决策，然后将决策下达至整个种群；
处于第二阶级的灰狼用β表示，称为从属狼，用于辅助α狼制定决策或其他种群活动；
处于第三阶段的灰狼用δ表示，侦察狼、守卫狼、老狼和捕食狼都是这一类；
处于第四等级的灰狼用ω表示，它们在灰狼群中扮演了"替罪羊"的角色，同时它们必须要屈服于其他等级的狼。

2.数学模型

2.1 等级制度

依据上述灰狼等级制度，可以对灰狼的社会等级进行数学建模，认为最合适的解是α，那么第二和第三最优解分别表示为β和δ，而剩余其他解都假定为ω。在GWO中，通过α、β和δ来导引捕食（优化），ω听从于这三种狼。

2.2 包围猎物

灰狼在捜索猎物时会逐渐地接近猎物并包围它，包围猎物的数学模型如下：

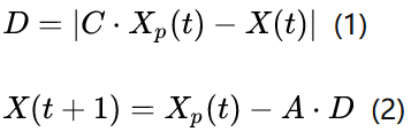
在这里插入图片描述
式(1)表示个体与猎物间的距离，式(2)是灰狼的位置更新公式。其中， t 是目前的迭代代数；Xp和X分别是猎物的位置向量和灰狼的位置向量；A，C是系数向量，它们的计算公式如下：

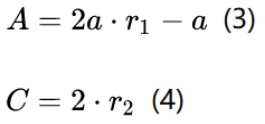
在这里插入图片描述
上式中，a是收敛因子，初始值为2随着迭代次数增大线性减小到0，r1和r2的模取[0，1]之间的随机数。

2.3 狩猎

灰狼具有识别潜在猎物（最优解）位置的能力，但很多问题的空间特征是未知的，因此灰狼无法确定猎物（最优解）的精确位置。为了模拟整个过程，这里假设α、β和δ识别潜在猎物位置的能力较强，所以，在每一次的迭代过程中，将保留当前种群中的最好三只灰狼（α、β和δ），然后再根据它们的位置信息来更新其它搜索代理（包括ω）的位置。

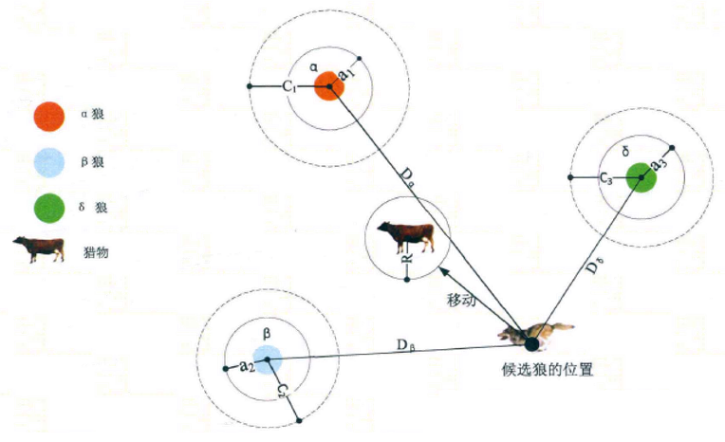
在这里插入图片描述

灰狼个体跟踪猎物位置的数学模型描述如下：

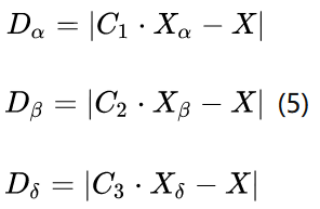
在这里插入图片描述

这三个式子分别表示了α，β和δ与其他个体之间的距离，Xα，Xβ和Xδ分布表示了这三匹狼当前的位置，C1，C2和C3是随机向量，X表示当前灰狼的位置。

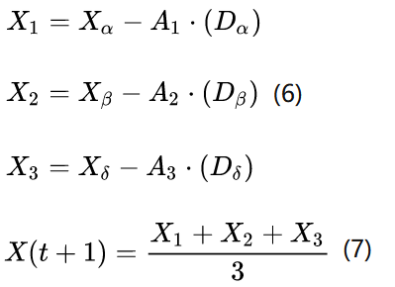
在这里插入图片描述

X1，X2和X3计算的是狼群中ω狼向α，β和δ前进的步长以及方向，式(7)定义的是ω的最终位置。

2.4 攻击猎物

当猎物停止移动时，灰狼通过攻击来完成整个狩猎过程。为了模拟逼近猎物，a值的减少会引起A的值也随之波动，也就是说，在a由2收敛至0的过程中，A在区间［-a，a］内变化。

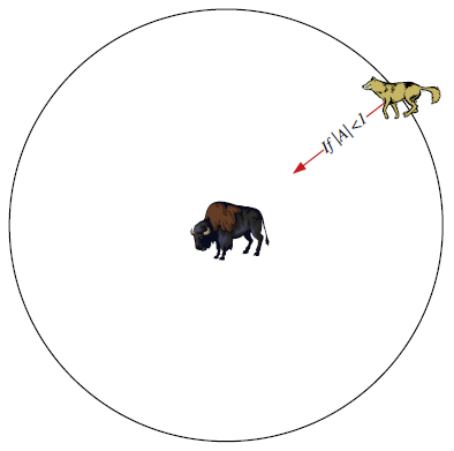
在这里插入图片描述

如上图，当A的值位于区间内时，灰狼的下一位置可以位于其当前位置和猎物位置之间的任意位置。当｜A｜＜１时，狼群向猎物发起攻击(陷入局部最优)，当｜A｜＞１时，灰狼与猎物分离，希望找到更合适的猎物(全局最优)。

2.5 寻找猎物

灰狼主要依据α，β和δ的位置信息来寻找猎物，它们开始会分散地去搜索猎物位置信息，然后集中起来攻击猎物。基于数学模型的散度，可以通过｜A｜＞１迫使捜索代理远离猎物，这种方式使得灰狼优化算法可以在全局寻找最优解。同时，GWO 算法中的另一个搜索系数是Ｃ。从式(4)可知，Ｃ是［０，２］之间的随机值，此系数表示灰狼当前位置对猎物影响的随机权重，Ｃ＞１是增加，反之减少。这有助于 GWO 在优化过程中展示出随机搜索行为，避免算法陷入局部最优。

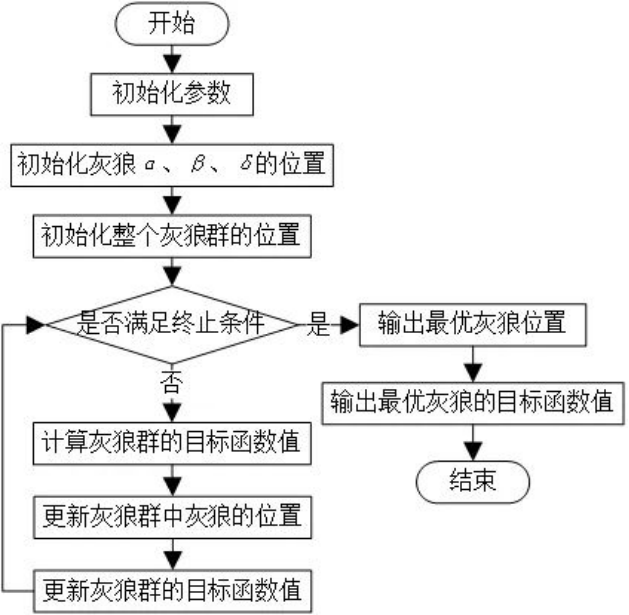
3.算法流程

简单的讲，狼群中有α，β和δ三只灰狼做头狼，α是狼王，β、δ分别排第二第三，β要听老大α的，δ要听α、β的。这三头狼指导着狼群里其他的狼寻找猎物，狼群寻找猎物的过程就是我们寻找最优解的过程。

具体的算法流程如下图：

在这里插入图片描述

4.算法优缺点

4.1 优点

1.算法操作简单
2.参数设置少
3.鲁棒性强
4.收敛速度相对同类算法更快
5.精确度较高

4.2 缺点

1.种群多样性差
2.后期收敛速度慢
3.易陷入局部最优

5.总结

目前有很多研究者，针对灰狼优化算法的不足之处提出了对应的改进算法，也发表一些论文，比如通过反向学习策略优化初始化种群分布以此增加全局搜索能力，还有学者通过引入混沌算子、设置算法参数更新控制变量，以应对灰狼优化算法后期收敛速度慢、可能陷入局部最优解的缺点。

6. 代码

GWO代码：

# -*- coding: utf-8 -*-
"""
Created on Mon Jul 17 11:24:36 2023

@author: zqq
"""


import numpy as np
import matplotlib.pyplot as plt

class GWO:
    def __init__(self):
        self.wolf_num = 15
        self.max_iter = 150
        self.dim = 30
        self.lb = -30*np.ones((self.dim,))
        self.ub = 30*np.ones((self.dim,))
        self.alpha_pos = np.zeros((1,self.dim))
        self.beta_pos = np.zeros((1, self.dim))
        self.delta_pos = np.zeros((1, self.dim))
        self.alpha_score = np.inf
        self.beta_score = np.inf
        self.delta_score = np.inf
        self.convergence_curve = np.zeros((self.max_iter,))
        self.position = np.zeros((self.wolf_num,self.dim))

    def run(self):
        count = 0
        self.init_pos()
        while count < self.max_iter:
            for i in range(self.wolf_num):
                flag_ub = self.position[i,:] > self.ub
                flag_lb = self.position[i,:] < self.lb
                self.position[i,:] = self.position[i,:]*(~(flag_lb+flag_ub))+flag_ub*self.ub+flag_lb*self.lb
                fitness = self.func(self.position[i,:])
                if fitness < self.alpha_score:
                    self.alpha_score = fitness
                    self.alpha_pos = self.position[i,:]
                elif fitness < self.beta_score:
                    self.beta_score = fitness
                    self.beta_pos = self.position[i,:]
                elif fitness < self.delta_score:
                    self.delta_score = fitness
                    self.delta_pos = self.position[i,:]
            a = 2 - count*(2/self.max_iter)
            for i in range(self.wolf_num):
                for j in range(self.dim):
                    alpha = self.update_pos(self.alpha_pos[j],self.position[i,j],a)
                    beta = self.update_pos(self.beta_pos[j], self.position[i, j], a)
                    delta = self.update_pos(self.delta_pos[j], self.position[i, j], a)
                    self.position[i, j] = sum(np.array([alpha, beta, delta]) * np.array([1/3,1/3,1/3]))
            count += 1
            self.convergence_curve[count-1] = self.alpha_score
        self.plot_results()

    def init_pos(self):
        for i in range(self.wolf_num):
            for j in range(self.dim):
                self.position[i,j] = np.random.rand()*(self.ub[j]-self.lb[j])+self.lb[j]

    @staticmethod
    def update_pos(v1,v2,a):
        A = 2*np.random.rand()*a-a
        C = 2*np.random.rand()
        temp = np.abs(C*v1-v2)
        return v1 - A*temp

    def plot_results(self):
        plt.style.use('seaborn-darkgrid')
        plt.plot(range(1,self.max_iter+1),self.convergence_curve,'g.--')
        plt.xlabel('iteration')
        plt.ylabel('fitness')
        plt.title('GWO fitness curve')
        plt.show()

    @staticmethod
    def func(x):
        dim, s = 30, 0
        for i in range(len(x)-1):
            s += 100*(x[i+1]-x[i]**2)**2+(x[i]-1)**2
        return s

if __name__ == "__main__":
    gwo = GWO()
    gwo.run()