目录

💥1 概述

1.1 电价伸缩系数分析

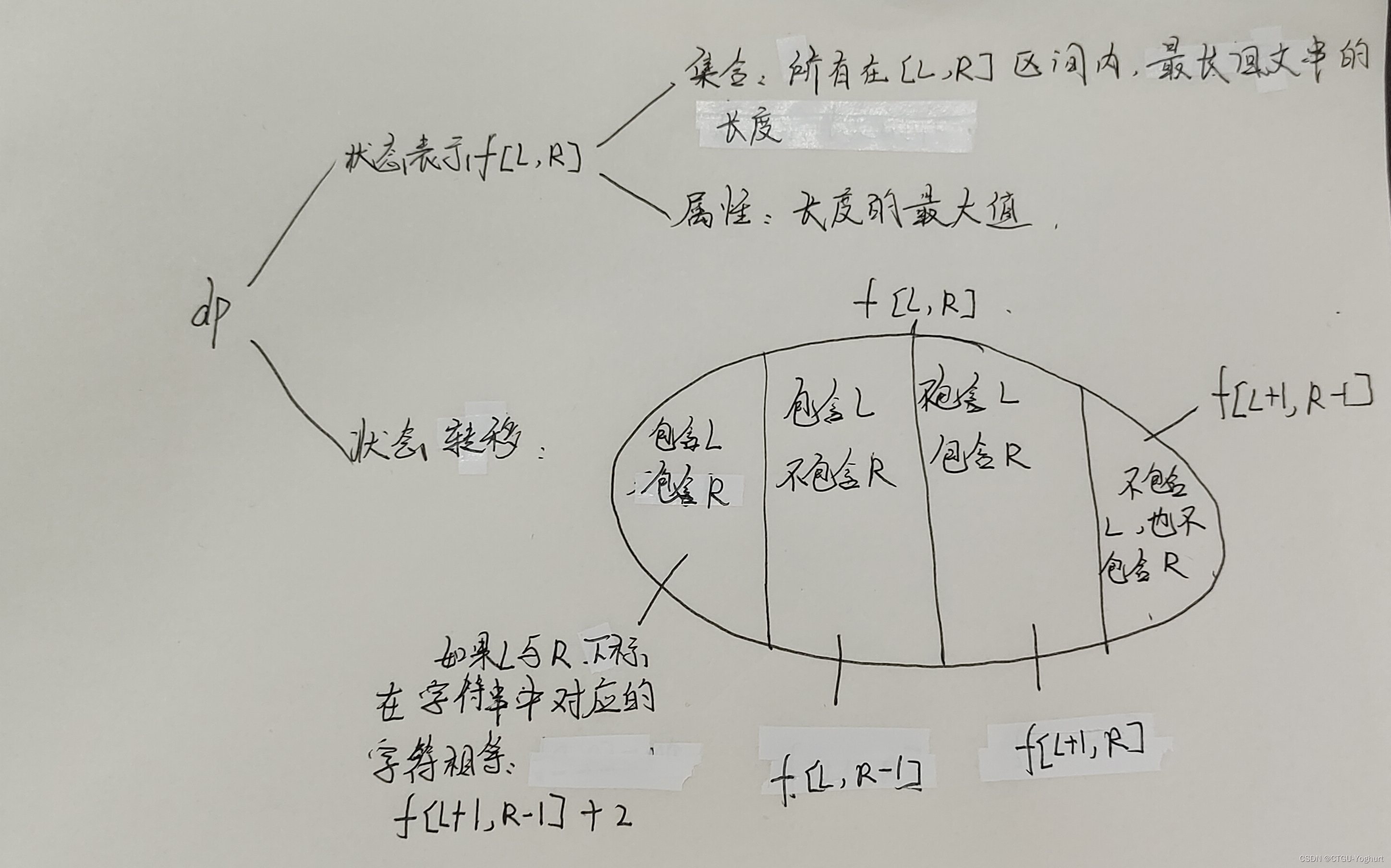
1.2 需求侧响应数学模型 

1.3 粒子群算法求解 

1.4 本文流程图 

📚2 运行结果

2.1 风电和光伏的出力情况

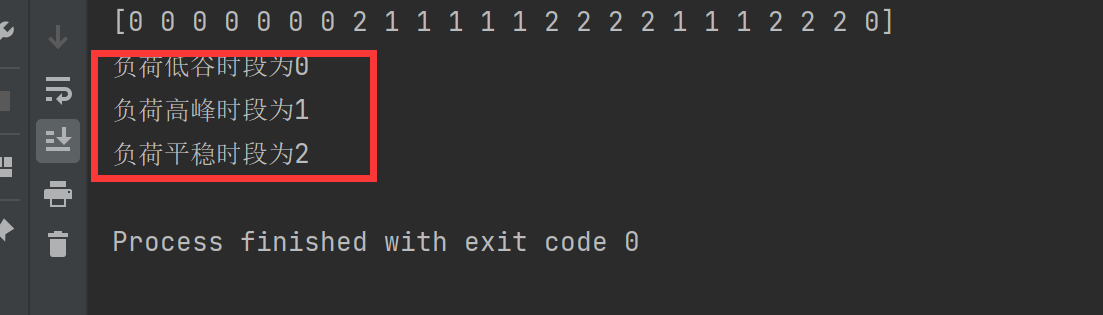
2.2 峰谷时段分类 

2.3 分时电价制定及负荷响应结果 

2.3.1 仅考虑需求响应

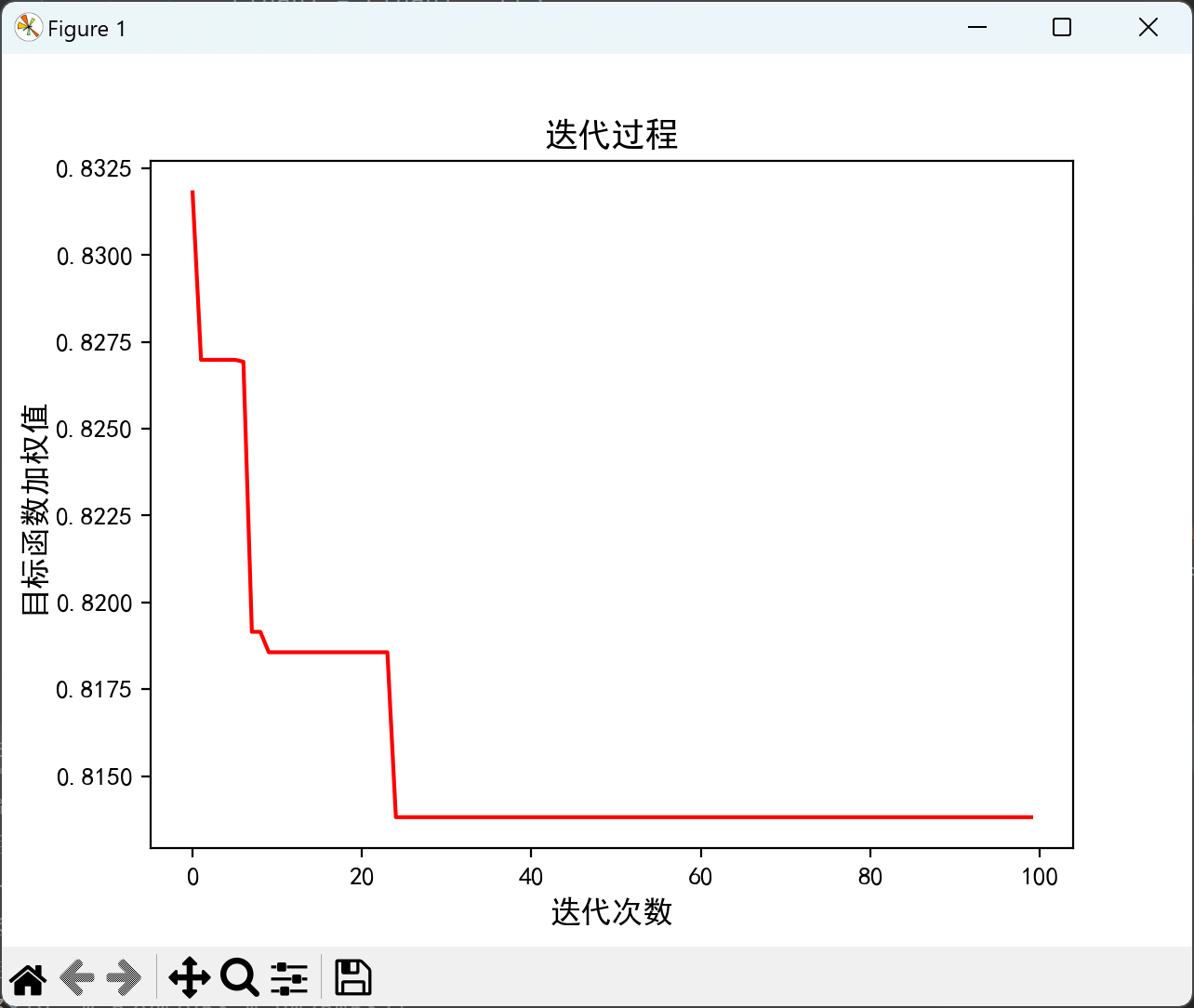
2.3.2 考虑分布式和需求响应 

🎉3 参考文献

🌈4 Python代码、数据、文章讲解

---

💥1 概述

在配电网中，需求侧响应是一种通过激励用户在供电能力不足时减少用电量的策略。为了对配电网的供电能力进行综合评估，需要考虑以下几个方面：

1. 预测需求：根据历史数据和相关因素（如天气、季节等），预测未来的电力需求量。

2. 需求响应机制：制定需求响应机制，包括激励机制和合同设计，以鼓励用户减少用电量。

3. 用户参与度：评估用户参与需求响应的程度，包括参与率和减少用电量的程度。

4. 可靠性分析：分析需求响应对供电能力和系统可靠性的影响，评估在需求响应情况下是否能满足用户的电力需求。

5. 成本效益分析：评估需求响应机制的效益，包括节约的电力成本、减少的供电设备需求和改善的系统可靠性等方面。

通过对需求侧响应的配电网供电能力进行综合评估，可以为电力公司制定更有效的需求响应策略和合同设计提供依据，以实现可持续的供电和优化的系统运行。

1.1 电价伸缩系数分析

在经济学领域，通常采用价格伸缩系数来描述商品的需求对于价格敏感程度[50] 。电力能源作为商品，同样可以采用伸缩系数来描述电力需求和电价之间的关系。一方面，电价的变化可以影响电力客户的用电行为，进而影响用电量；另一方面，客户用电量的改变，也可以指导供电侧电价的制定，使电力企业获得更高的收益。客户用电量与电价之间的关系采用电价伸缩系数 k 来表示。k 可以定义为客户用电量波动率与价格波动率的比值，如式(2-17)：

式中，p 和 m 分别表示该时刻初始的用电量和价格，∆p和∆m 分别表示该时刻的用电量和电价的改变量。实际生产生活中，电力客户的用电行受多重因素影响。一方面，当前时段电力价格的变化可能会导致当前时段用电行为的改变，产生了用电量的增减；同时，其他时段的电价变化也会对当前时段客户的用电行为产生影响，即产生了用电量的转移。所以，在分析价格伸缩性时，需要综合考虑上述两种伸缩变化[51] 。可定义第 i 时段的自伸缩系数为kii，第 i 时段对第 j 时段的互伸缩系数为kij，如式(2-18)~式(2-19)。在得到自伸缩系数kii和互伸缩系数kij后，则能形成需求侧响应电价伸缩系数矩阵 K，如式(2-20)：

 

显然地，K 矩阵对角线元素k ff 、 k pp 、kgg 表征了当前时间电价变化与需求侧用电量之间的相互作用，是自伸缩系数；而矩阵中其他元素则表征了不同时间内电价变化与需求侧用电量的相互作用，是互伸缩系数。进一步地，在采用了分时电价之后，各个时间段用电变化量ΔP ，如式(221)：

 

1.2 需求侧响应数学模型 

对于配电网而言，如果在其允许的范围内峰值负荷过大，会导致其转带备用容量不足，负荷波动率较高，容易影响该配电网的稳定性[52] 。同时，文献[53]通过柯西-施瓦茨不等式证明了网损与最高-最低负荷比率成正比，即日内负荷的峰谷差越小，系统线损率越低。可见，缩小电网的高低负荷比率能够有效降低网损，提高系统负荷率，从而提升设备利用率。

基于上述分析，设置日最高负荷与日最高-最低负荷比率为规划目标。因为这两个目标可以从直观上判断出系统的供电能力，故也可以定义这两个规模目标为系统的显性供电能力，其值越小，系统的显性供电能力越好。规划目标如式(2-23)~式(2-24)：

(1) 主观限制 

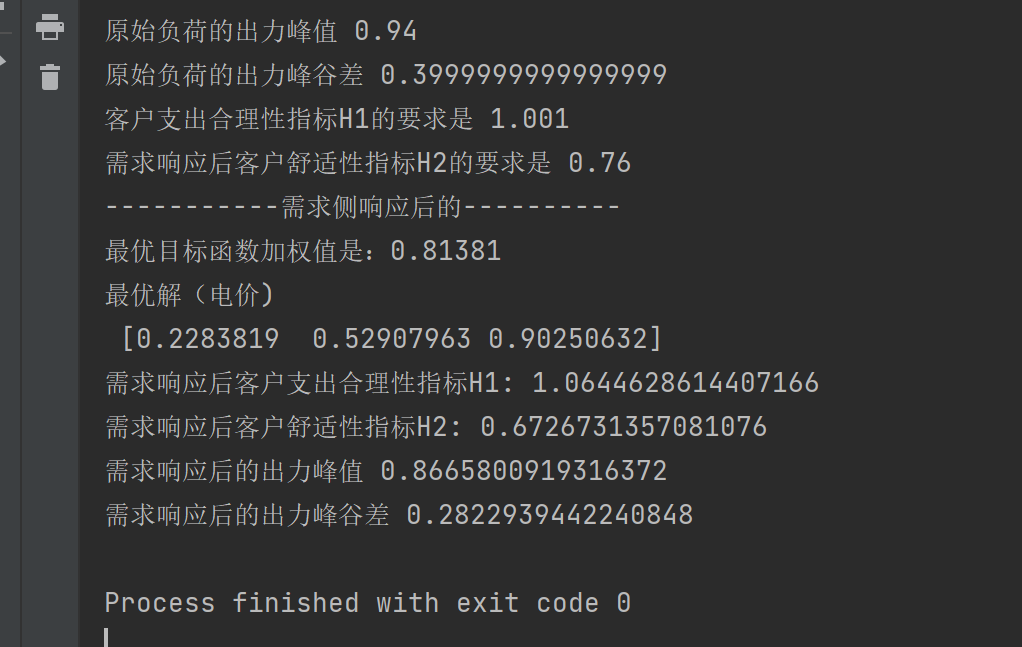
某些时段过高的价格会导致客户支出过高，所以需要考虑客户负担的合理性，即在应用需求侧响应策略后客户所需负担的总费用不应升高。据此，定义客户支出合理性指标 H1，如式(2-26)：

同时，在市场经济中，欲达到供需双方利益的最大化，不仅需要考虑商品的成本和用户的支出，同时也需要考虑商品是否满足需求方的舒适性。分析需求侧响应策略的削峰填谷作用可知，微观上，在采用需求侧响应策略之后，一部分客户会根据分时电价调整自身的用电安排，这会导致自身的舒适性降低，而使个人日用电需求曲线变的平缓；宏观上，电力日负荷曲线是全体电力客户当日用电情况的集中反映，当部分用户因参与需求侧响应而使得用电曲线变的平缓时，电网的日负荷曲线会随之变的平缓，日负荷标准差也会相应减小。

通过上述分析可知，负荷曲线的标准差可以从一定程度上体现客户对于需求侧响应的参与度。随着参与度的提升，负荷曲线的标准差也会在一定程度上减小，但是客户被迫调整或者削减原有的用电安排的情况就会越多，导致舒适性降低。基于上述分析，定义客户舒适性指标 H2如式(2-27)：

 

(2) 客观限制 

根据经济学相关知识可知，通常情况下商品的价格量是一个合理范围内的正数；同时，对于客户而言，为保证正常的生产生活用电需求，电力负荷高峰时的电费不可以过高；而对于供电企业而言，为保证盈利，则在电力负荷低谷时电费不能过低；此外，根据电力市场相关经验易知，商品定价时需要保证一定的价格梯度，即低谷时刻价格须比平时价格低，且平时价格也须比高峰时段价格低。客观价格边界条件如式(2-31)：

1.3 粒子群算法求解 

粒子群优化算法(Particle Swarm Optimization，PSO)属于进化算法的一种[54] 。这种算法与模拟退火算法相似，它是从随机解出发，通过迭代寻找最优解，同时通过适应度来描述所得解的优劣。PSO 法与遗传算法相比，不需要经过“交叉”和“变异”过程，而是跟踪当前搜索到的最优值来进行全局寻优。

PSO 算法中，每个规划目标的隐含解都是搜寻空间内的一枚粒子。所有粒子都存在由优化函数决定的适值，同时每个粒子还有一个速度决定它们“飞行”的方向和距离，全部粒子通过实时跟踪最优粒子在解空间中不断进行迭代。粒子的更新方式如图2-3 所示：

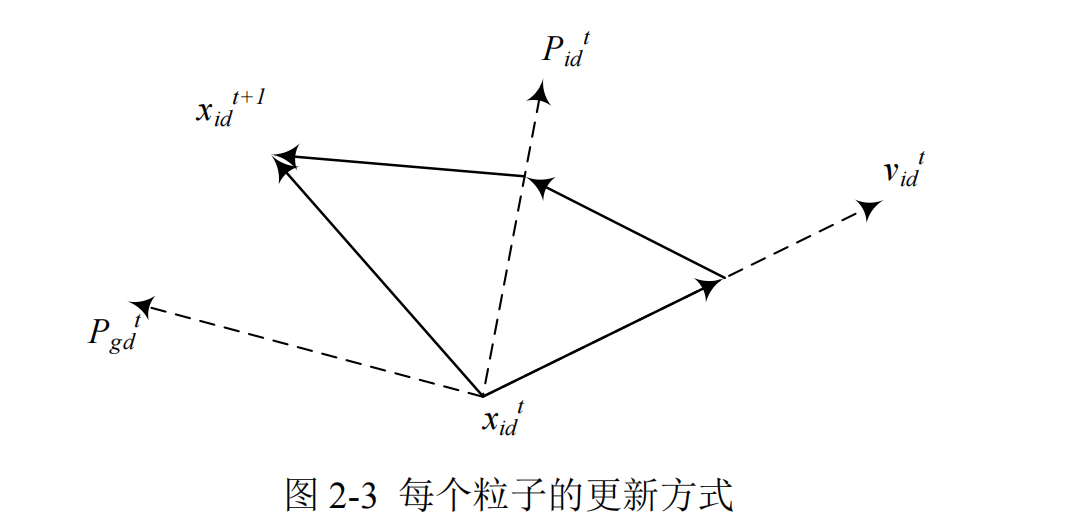
1.4 本文流程图 

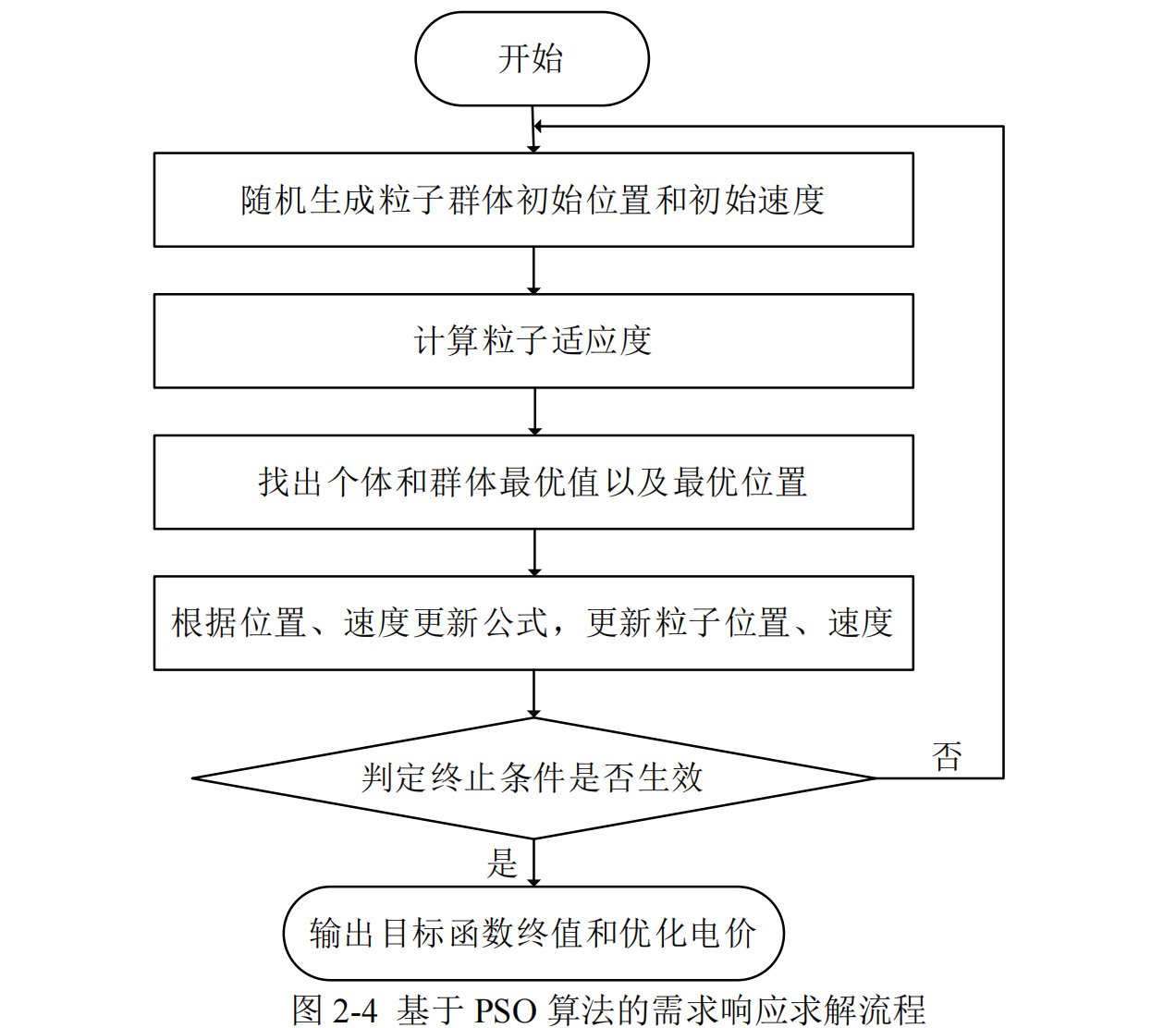
📚2 运行结果

2.1 风电和光伏的出力情况

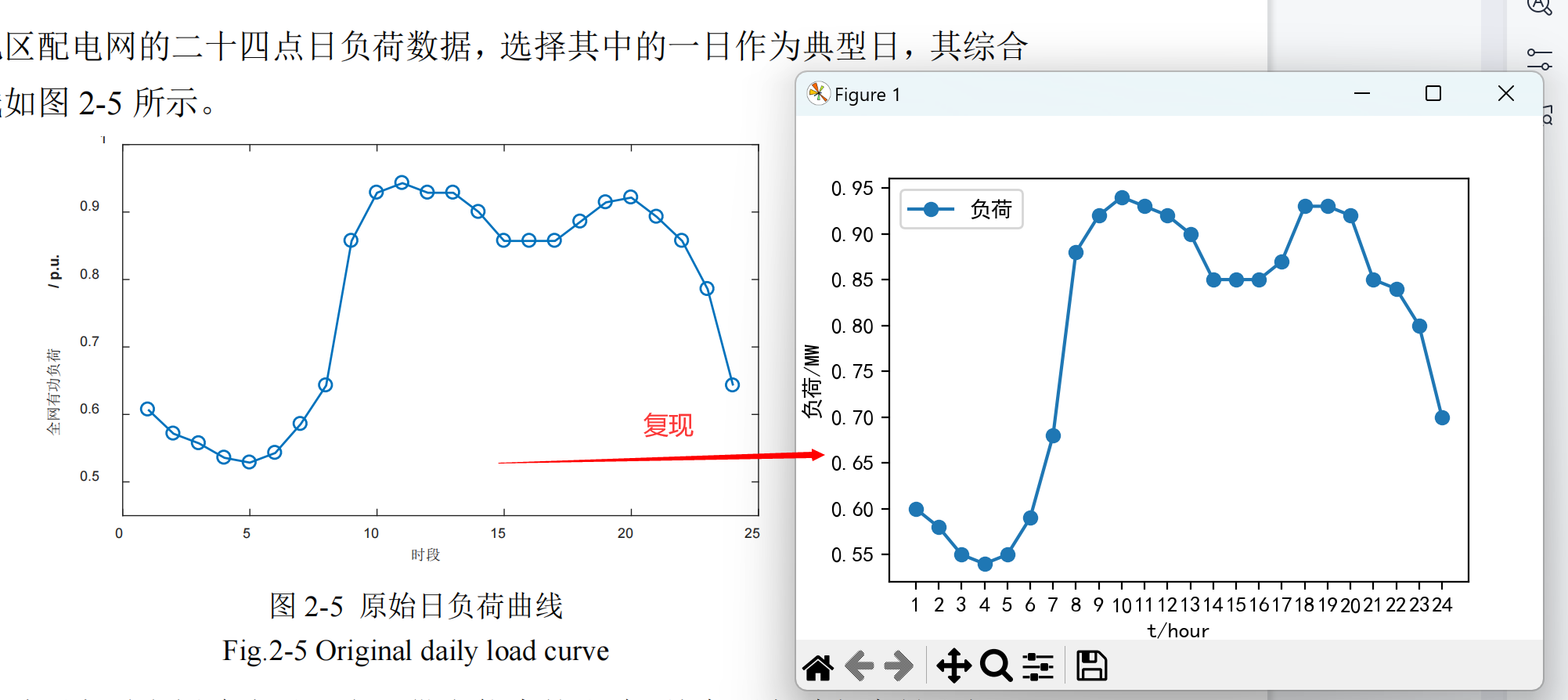
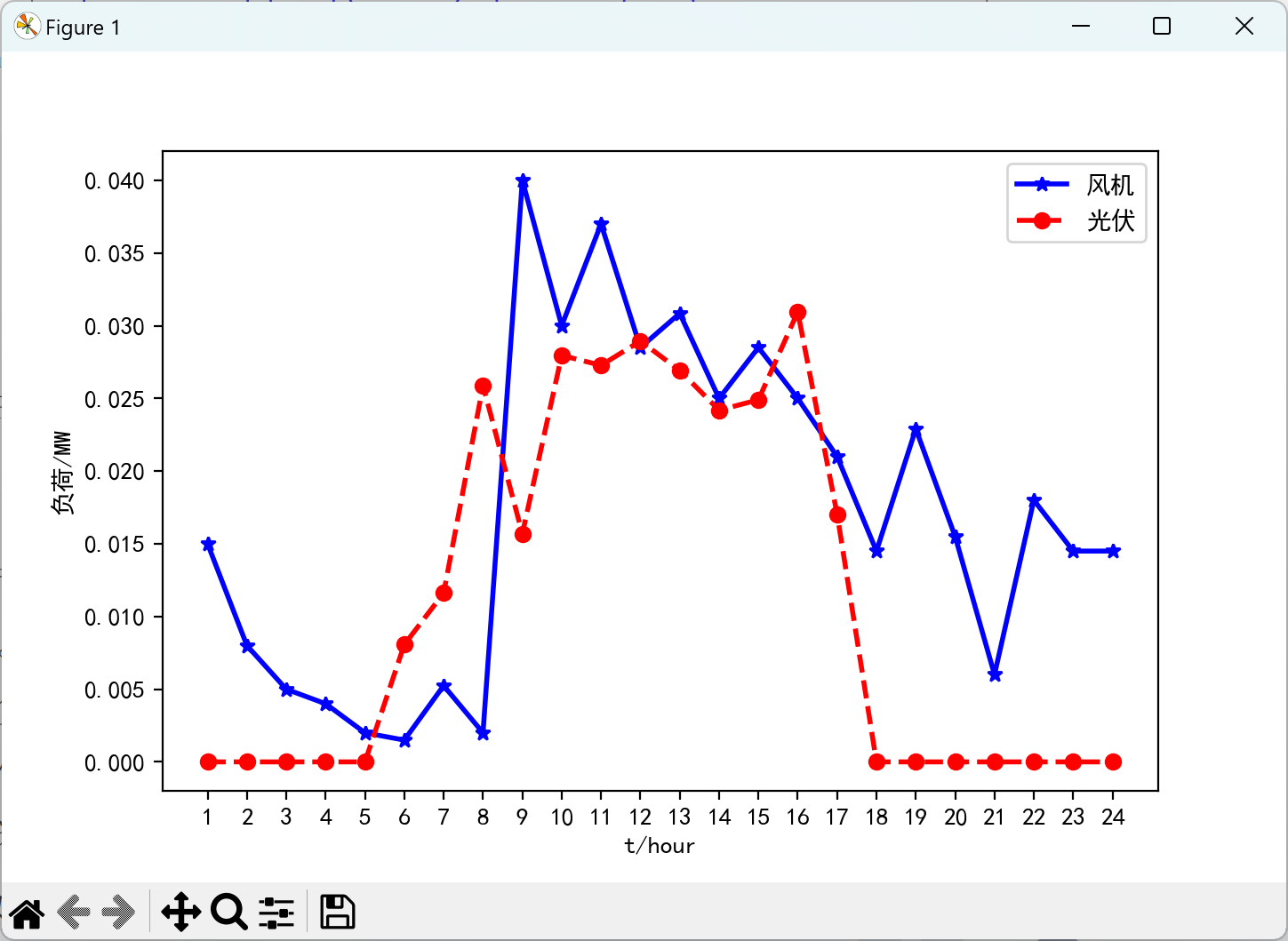
2.2 峰谷时段分类 

2.3 分时电价制定及负荷响应结果 

本文也是粒子群算法进行求解，对于需求侧响应后负荷的变化，可根据电价伸缩系数和式(2-21)~式(2-22)计算得出。伸缩系数在工程使用时需要结合历史运行数据和当地情况并由式(2-17)~式(2-19) 计算得出。本文选择伸缩系数矩阵如式(2-37) 

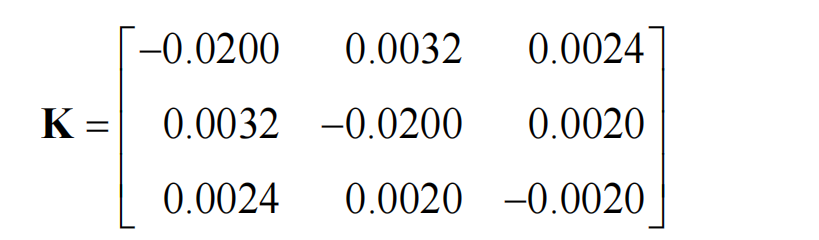
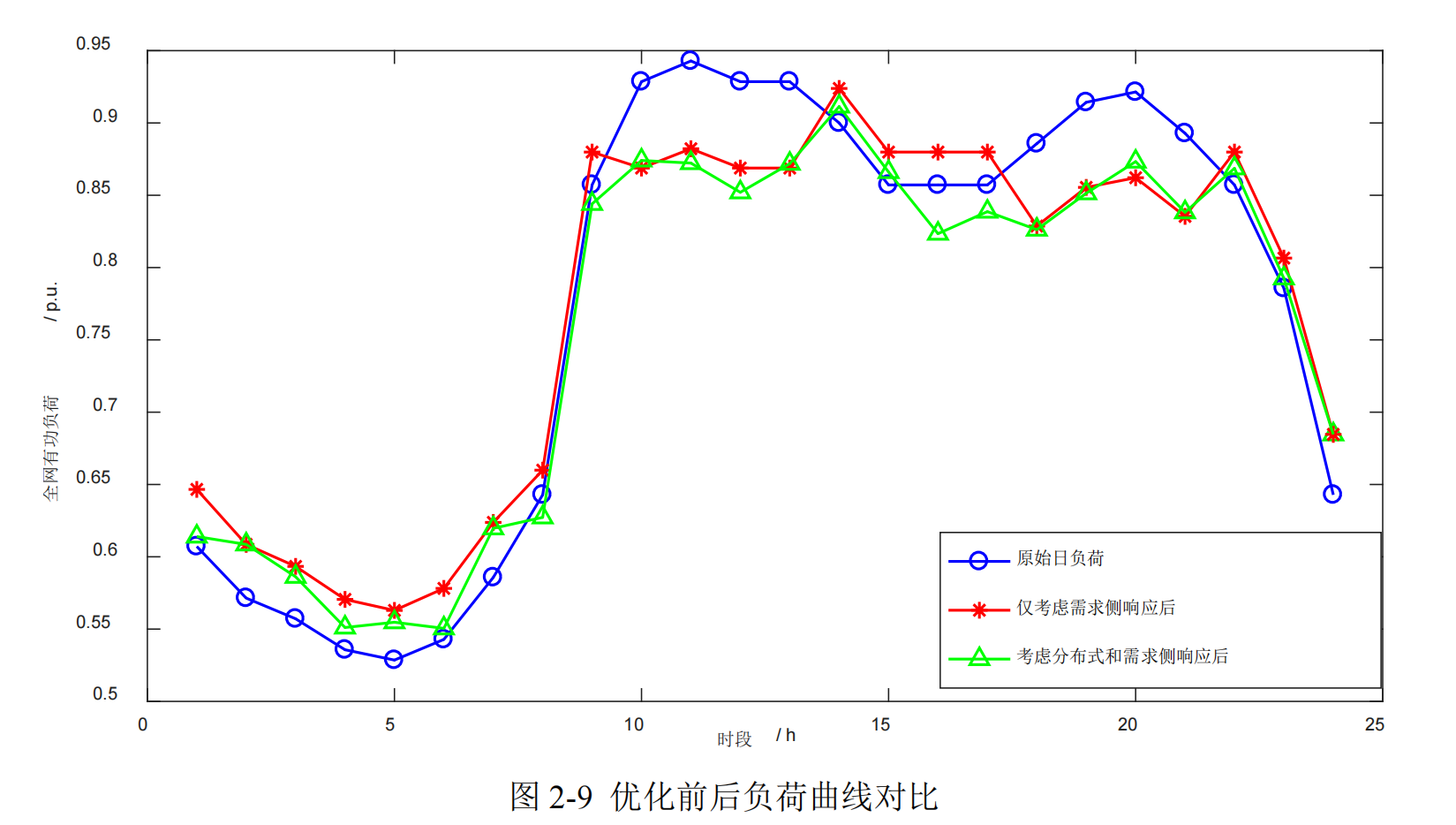
原文结果：

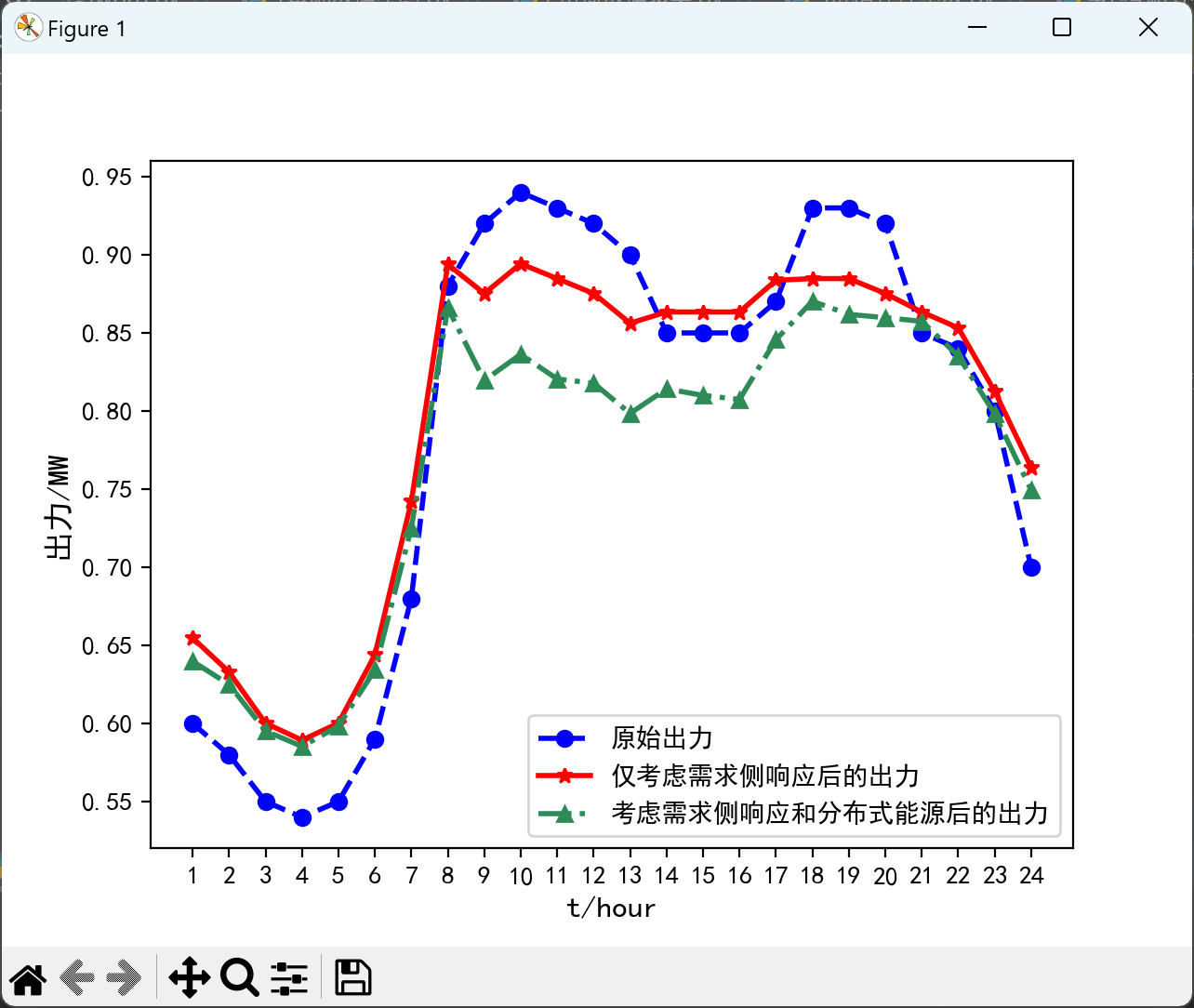
复现结果： 

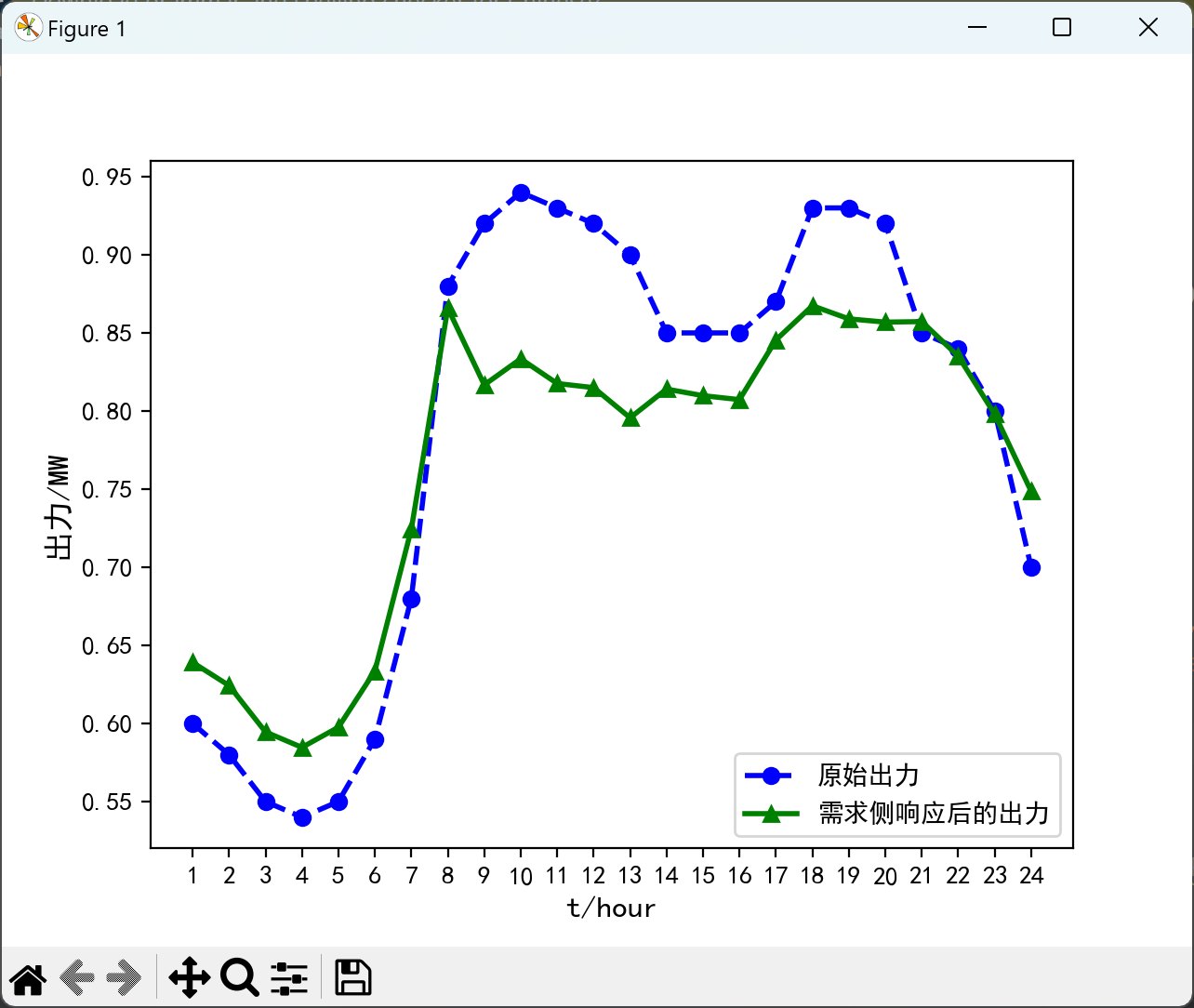
2.3.1 仅考虑需求响应

复现结果：

 

 

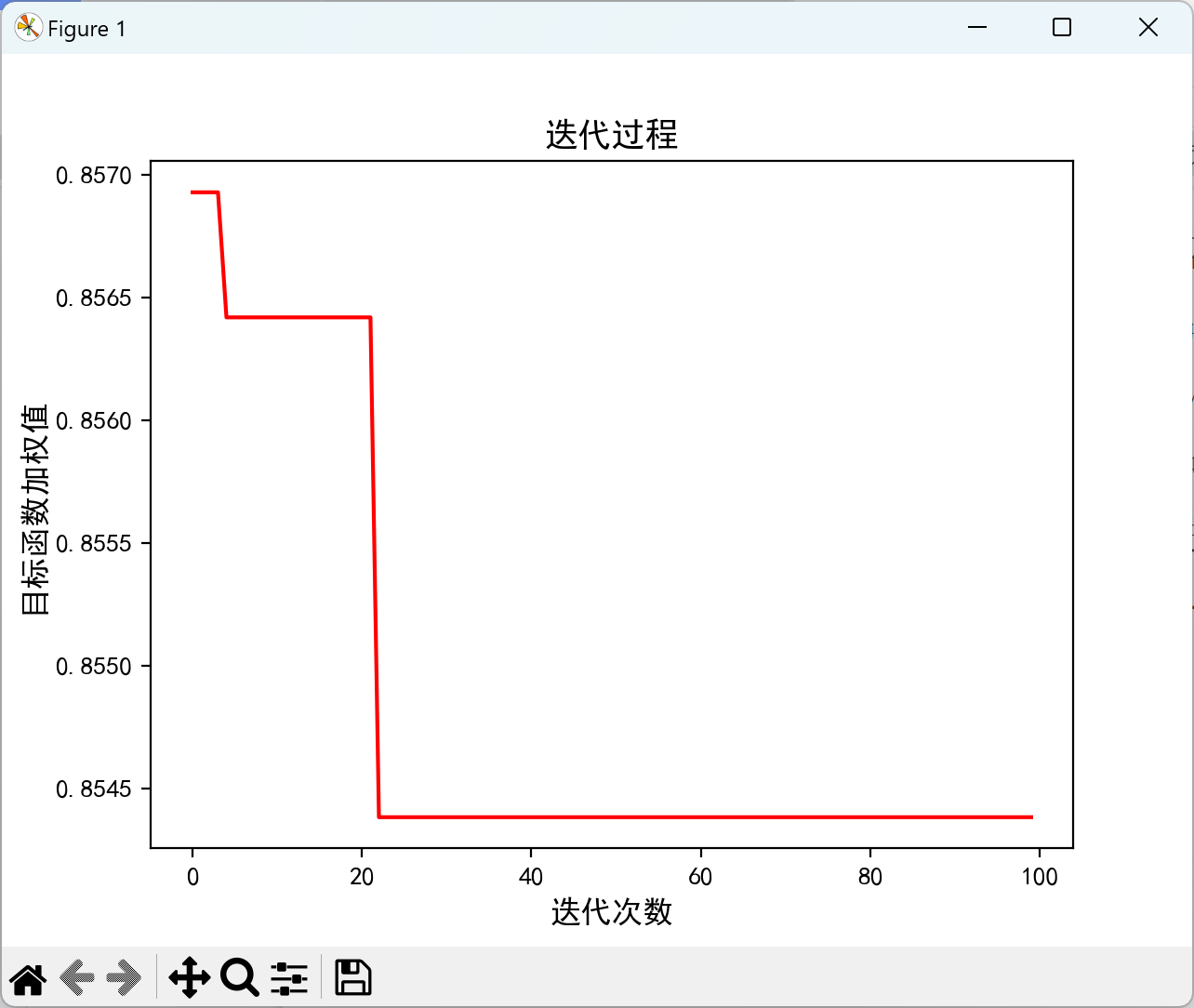
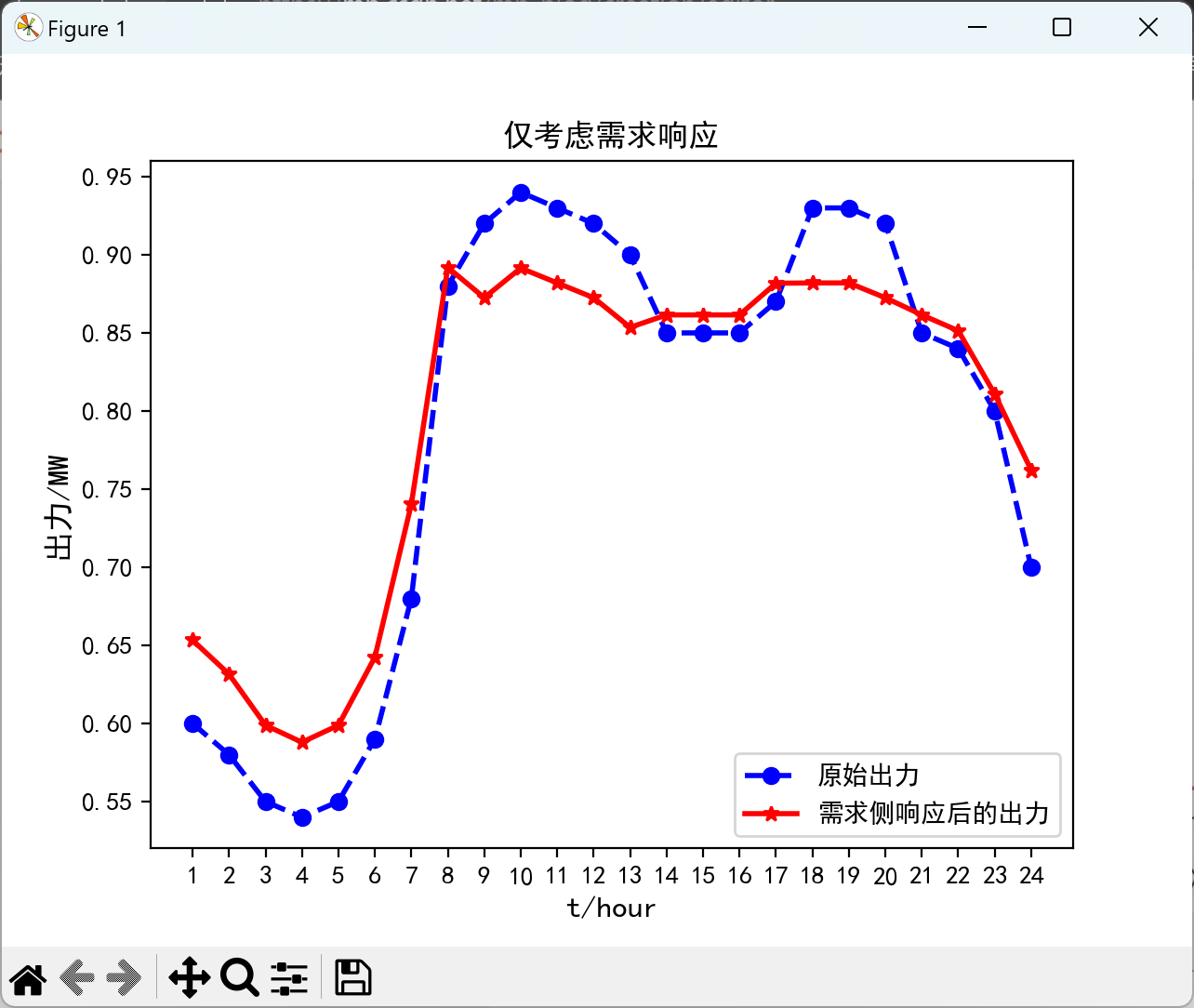
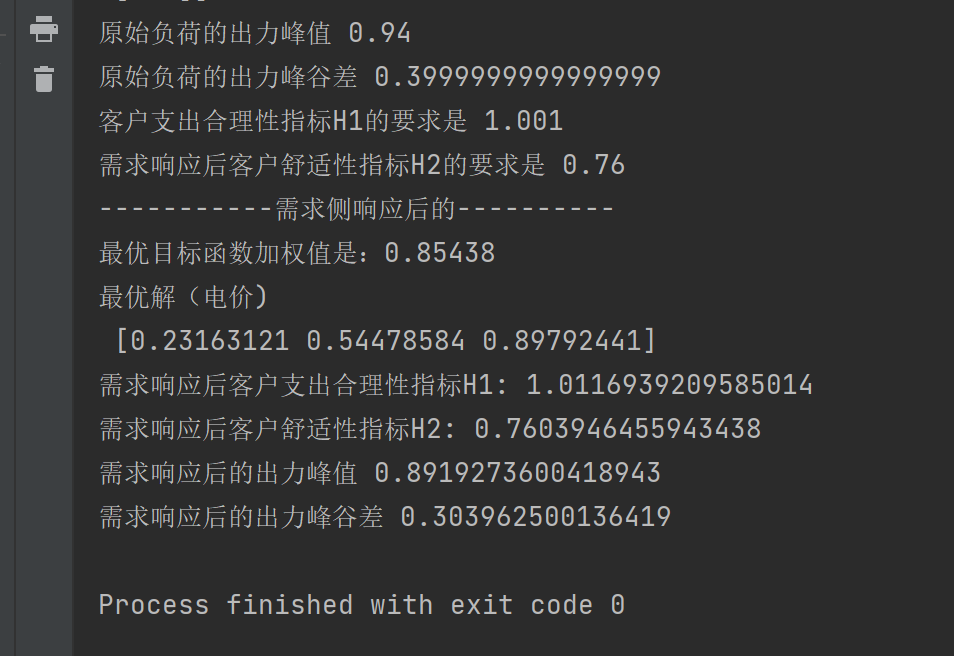
2.3.2 考虑分布式和需求响应 

 

🎉3 参考文献

部分理论来源于网络，如有侵权请联系删除。

[1]魏鹏飞. 基于需求侧响应的配电网供电能力综合评估[D].内蒙古工业大学,2019.

🌈4 Python代码、数据、文章讲解