概述

问题来源

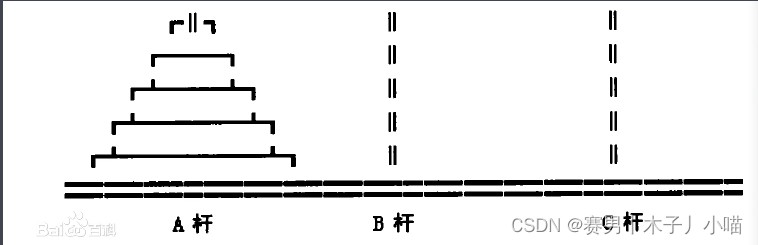
    汉诺塔（Tower of Hanoi），又称河内塔，是一个源于印度古老传说的益智玩具。大梵天创造世界的时候做了三根金刚石柱子，在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。

汉诺塔问题的规则

1. 有三根柱子，分别记为A、B、C。开始时，所有的盘子都放在A柱子上，按照从大到小的顺序堆叠。
2. 目标是将所有的盘子从A柱子移动到C柱子上，期间可以借助B柱子作为辅助。
3. 在移动过程中，每次只能移动一个盘子，并且大盘子不能放在小盘子上面。
4. 

实现

解题思路

1. 当只有一个盘子时，直接将盘子从A柱子移动到C柱子即可。
2. 当有多个盘子时，可以将问题划分为三个步骤：
   • 将上面的n-1个盘子从A柱子移动到B柱子（借助C柱子）；
   • 将最底下的一个盘子从A柱子移动到C柱子；
   • 将B柱子上的n-1个盘子移动到C柱子（借助A柱子）。

    这样问题解决了，但实际操作中，只有第二步可直接完成，而第一、三步又成为移动的新问题。以上操作的实质是把移动n个盘子的问题转化为移动n-1个盘，那一、三步如何解决？我将以1，2，3，n个盘子为例进行详细的讲解。

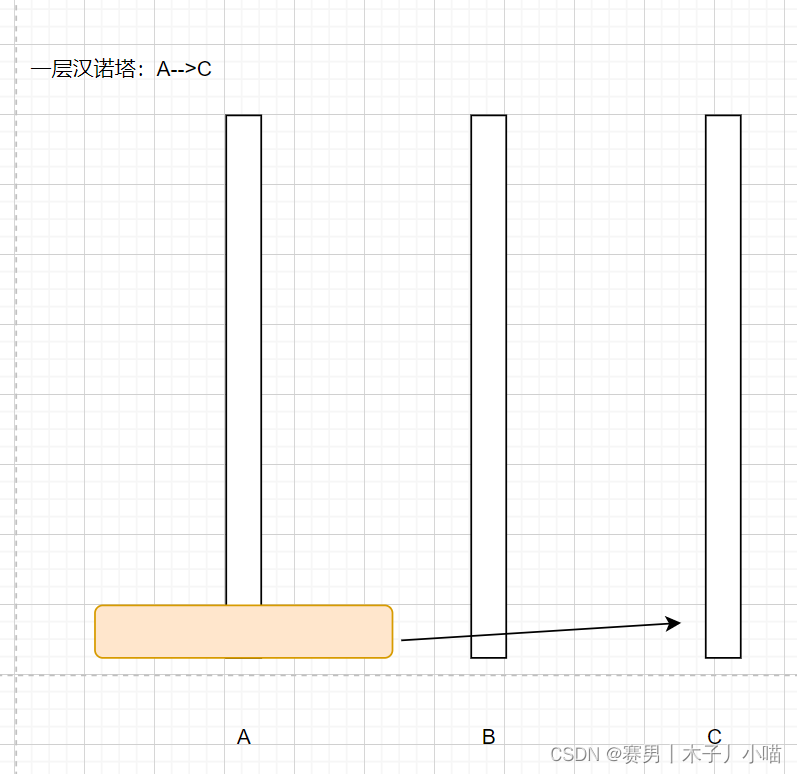
一个盘子

直接从A移动到C

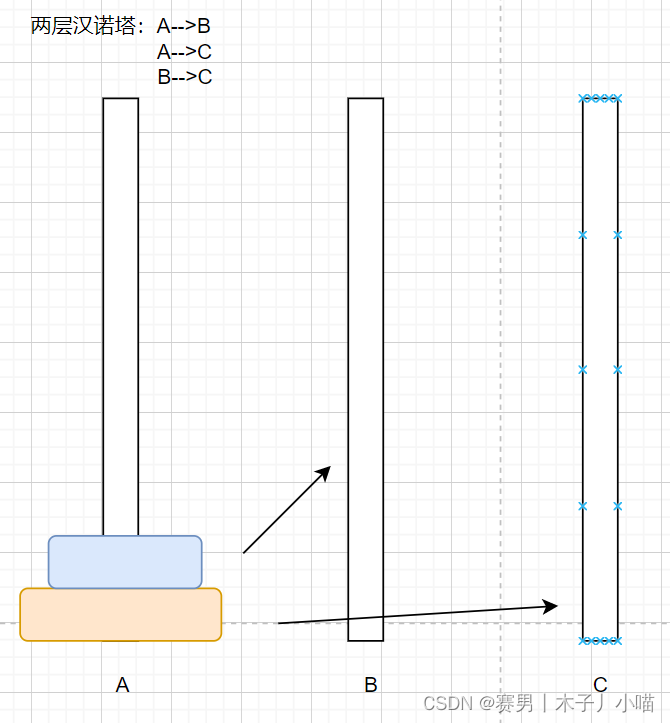
两个盘子

    先把小盘先移动到B,然后把大盘移动到C，最后把小盘也移动到C
    注意：当把小盘先移动到B之后，就可以看成分别移动两个盘，那移动每个盘的时候就是移动一个盘，方法就和上面的一个盘子移动是一模一样的，ABC的位置就是相对的，这一点很重要，对于后续理解代码非常重要!!!

整体移动图：

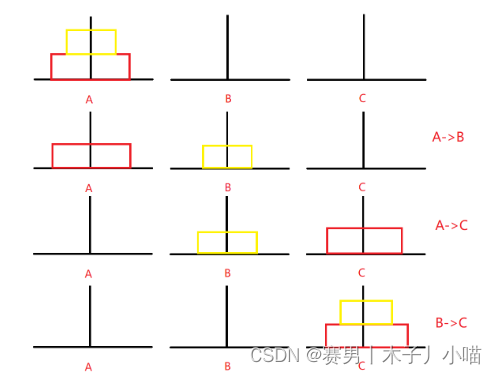
三个盘子

先把蓝色盘子作为一个整体移动（此时宏观上看就是两个盘子的移动）

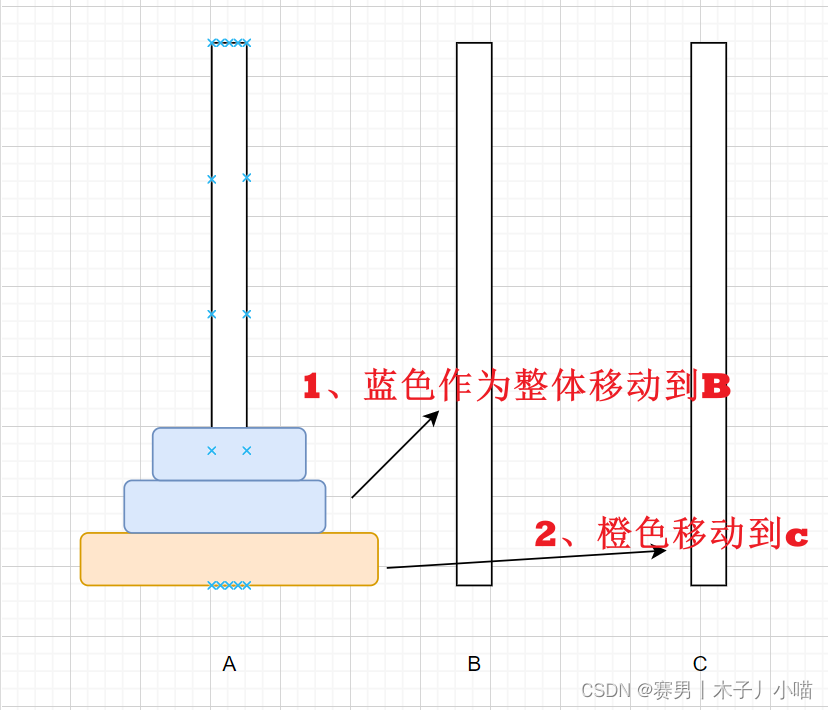
    橙色移动到目标柱之后，就不在思考它，先将它剔除，然后剩下的两个盘（微观），方法就和上面的两个盘子移动是一模一样的。

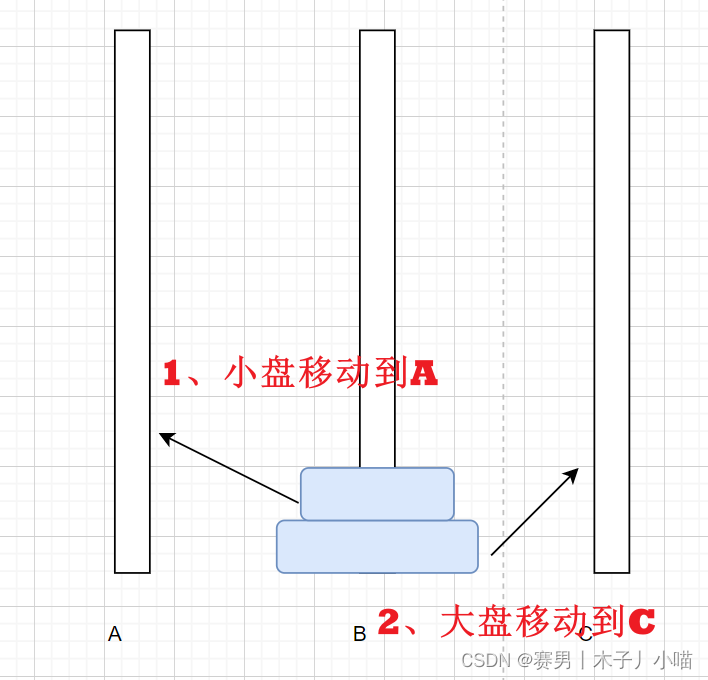
上面的过程总结一下如下图所示
    移动三个盘其实是先分成两组两个盘（第一组是宏观上，第二组是微观上，宏观微观请往上看）
接下来的两个盘又采用1个盘的挪动方法

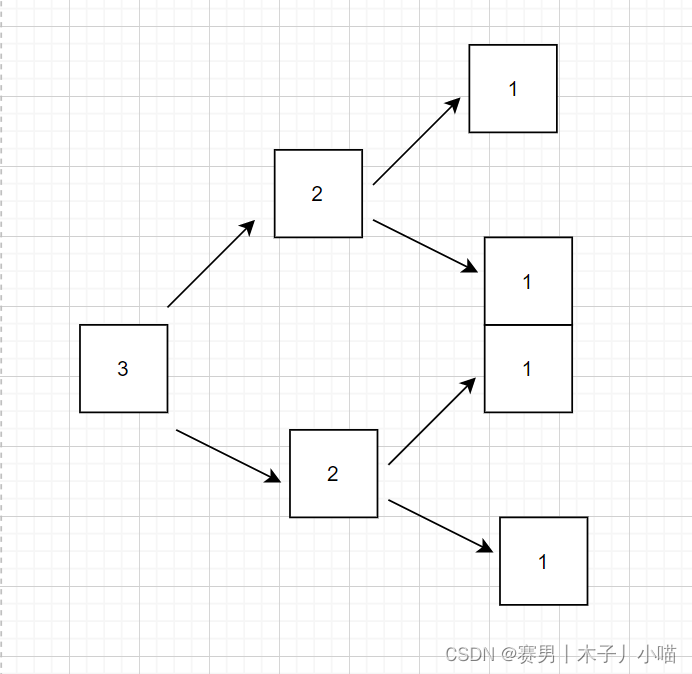
n个盘子

    同理，n个盘子先把上面的n-1个盘看成一个整体先移动到B上（先不管中间是如何操作的），再把第n个盘子移动到C上，再把n-1个盘放到c上

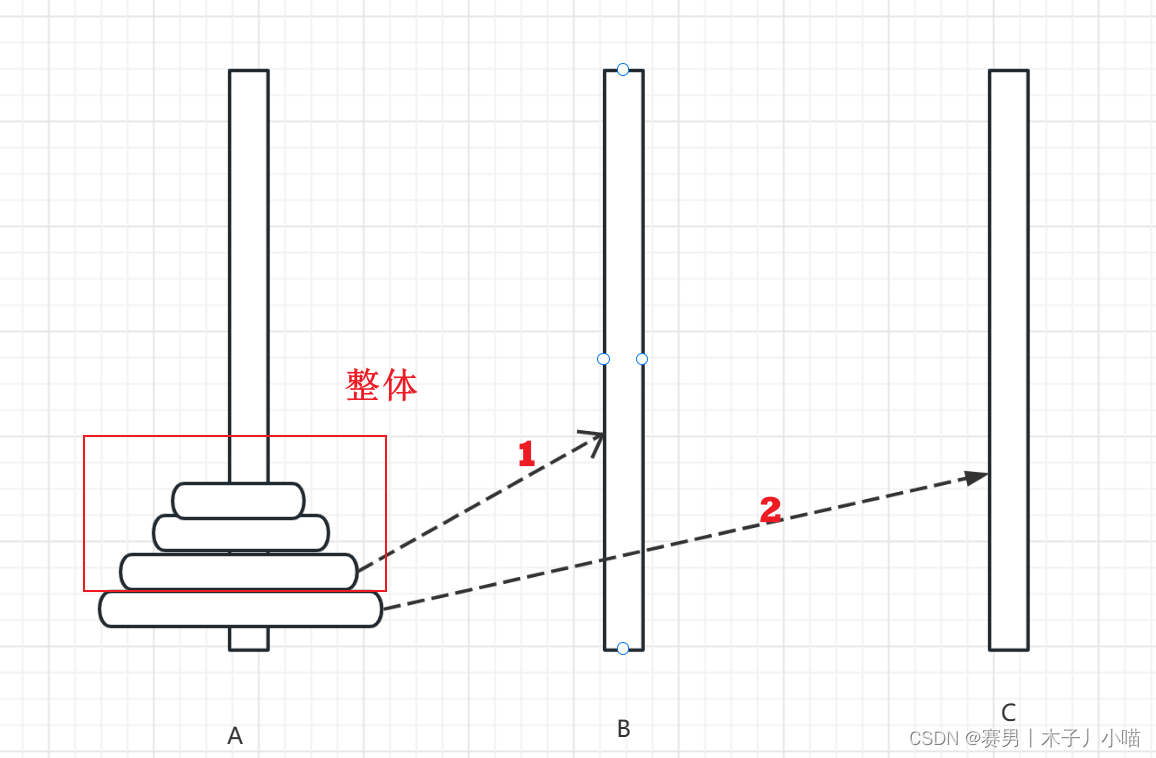
    接下来把移动到C上的盘忽略掉
    剩下的就有n-1个盘子，我们把上面的n-2个盘看成一个整体先移动到A上，再把第n-1个盘子移动到C上，再把n-2个盘放到c上

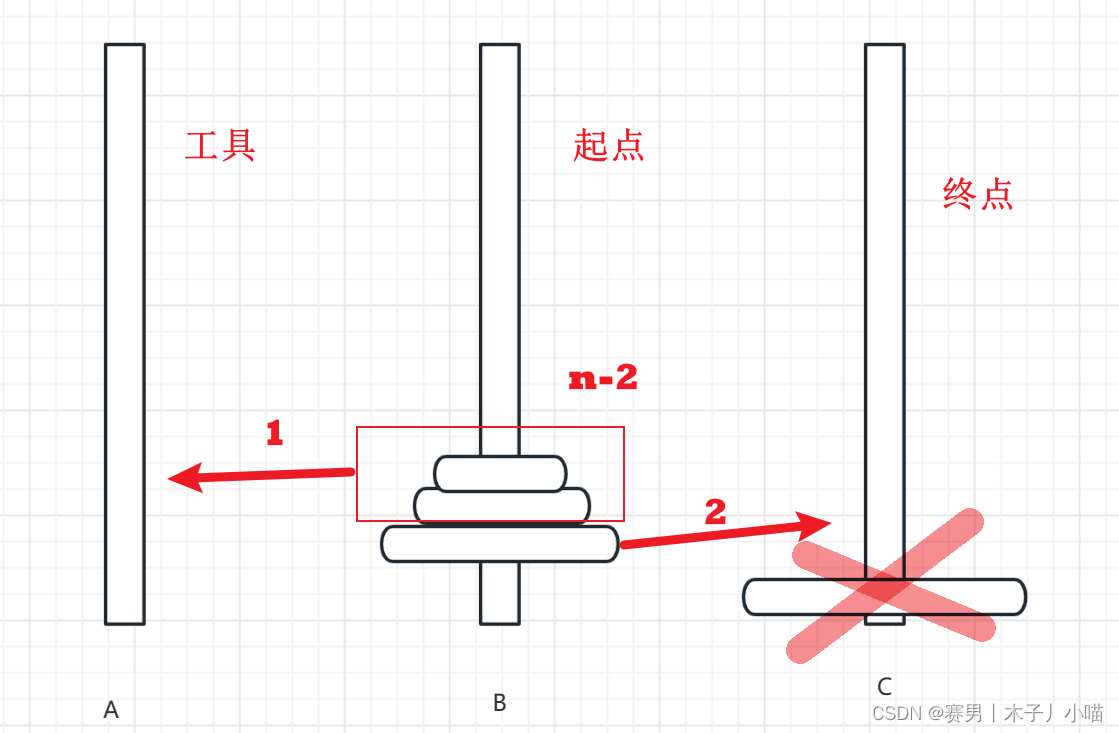
    为了便于大家理解，我把上面两端文字放在一起，对比给大家看，着重数以里面n的变化

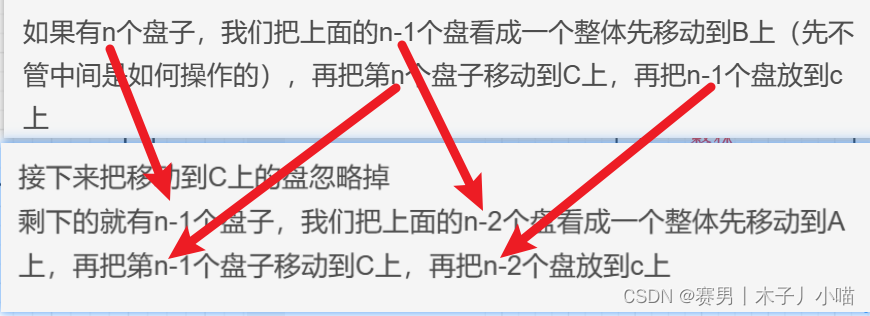
    注意：在这里，有起点柱、终点柱，和工具柱（用来中转用），这三个的位置在变换的过程中是相对的，并不是固定不变的。

递归

    从上面的分析过程来看，学过递归的同学，一定已经发现汉诺塔就是典型的递归问题
我们简单的了解一下递归

概念

    递归是一种解决问题的有效方法，在递归过程中，函数将自身作为子例程调用。
简单说程序调用自身的编程技巧叫递归。递归的思想是把一个大型复杂问题层层转化为一个与原问题规模更小的问题，问题被拆解成子问题后，递归调用继续进行，直到子问题无需进一步递归就可以解决的地步为止。

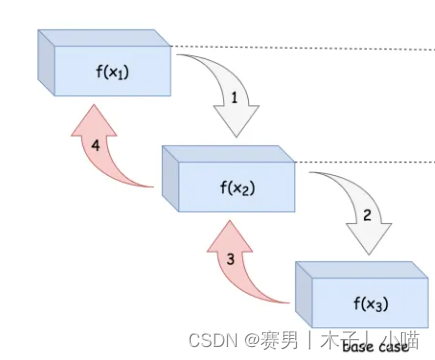
递归特性

    相比其他解法，递归只需少量程序就可描述出解题过程，大大减少了程序的代码量，而且很好理解。递归的能力在于用有限的语句来定义对象的无限集合。

递归的时间复杂度

    递归复杂度 O(T) 通常是递归调用的数量（记作 R） 和计算的时间复杂度的乘积（表示为 O(s)）的乘积：

O(T)=R∗O(s)

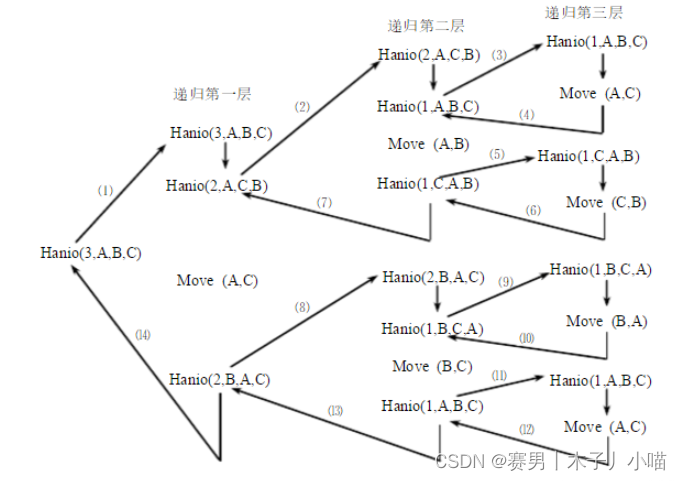
汉诺塔中的递归

    在汉诺塔问题中就是将 n 个圆盘分为 n-1 （即除最低层的圆盘）与 1 （即最底层的圆盘），将n-1个圆盘移动到中转位置，将1移动到目的位置，再将 n-1 分为 （n-1）- 1 与 1，将（n-1）- 1 移动到中转位置，将1移动到目的位置，依次类推…

代码

第一步：
把n-1个盘子 从A柱移动到B柱
把第n个盘子从A柱移动到C柱
第二步：
把n-1个盘子 从B柱移动到C柱

package algorithm.Hhanoi;

/**
 * @BelongsProject: myProject
 * @BelongsPackage: algorithm.hanoi
 * @Author:xiaonan
 * @CreateTime: 2023-07-19 09:08
 * @Description: TODO
 * @Version: 1.0
 */
public class HanoiTower {
    public static void main(String[] args) {
        int n=3;//盘子的数量
        char a='A';//A柱
        char b='B';//B柱
        char c='C';//C柱
        hanoi(n, a, b, c);
    }
    
/*第一步：
把n-1个盘子 从A柱移动到B柱
把第n个盘子从A柱移动到C柱
第二步：
把n-1个盘子 从B柱移动到C柱
注意：变的的是目标柱，终点柱和中转柱，不变的是柱号
*/
    public static void hanoi(int n,char a,char b,char c){
        if (n==1){
            System.out.println("将盘子从"+a+"移动到"+c);
        }
        else{
             将上面的n-1个盘子从A柱子移动到B柱子（借助C柱子）
            hanoi(n-1,a,c,b);
            // 将最底下的一个盘子从A柱子移动到C柱子
            System.out.println("将盘子从"+a+"移动到"+c);
            // 将B柱子上的n-1个盘子移动到C柱子（借助A柱子）
            hanoi(n-1,b,a,c);
        }
    }
}

    运行上述代码，可以得到输出结果（这表示将3层汉诺塔从柱子A移动到柱子C需要的步骤）：

    在上述代码中，hanoi函数是递归函数，它实现了汉诺塔问题的解决方案。在每一次递归调用中，问题规模都减小了1，直到问题规模为1时，递归终止。

总结

    汉诺塔问题实质是把移动n个盘子的问题转化为移动n-1个盘，依据该原理，层层递推，即可将原问题转化为解决移动n -2、n -3… … 3、2，直到移动1个盘的操作，而移动一个盘的操作是可以直接完成的。至此任务真正完成了。而这种由繁化简，用简单的问题和已知的操作运算来解决复杂问题的方法，就是递归法，汉诺塔问题是用递归方法求解的一个典型问题。
    如果大家还有什么问题，欢迎给我留言，我们一起讨论，非常感谢大家的阅读，如果觉得我的文章不错，请点赞收藏哦~