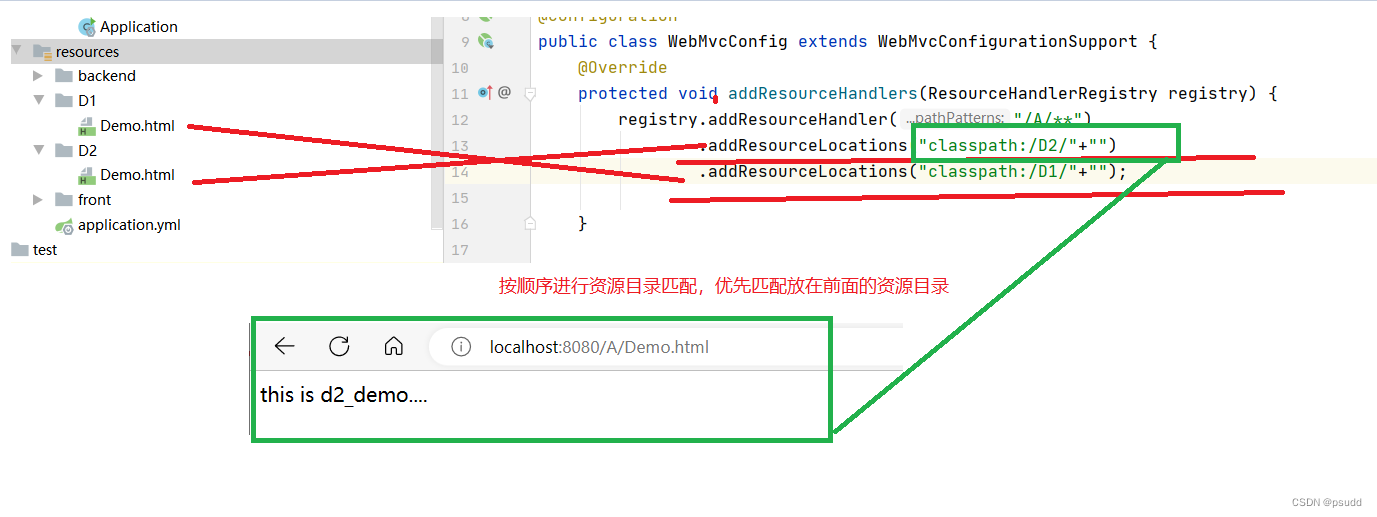
7.1 查找的基本概念

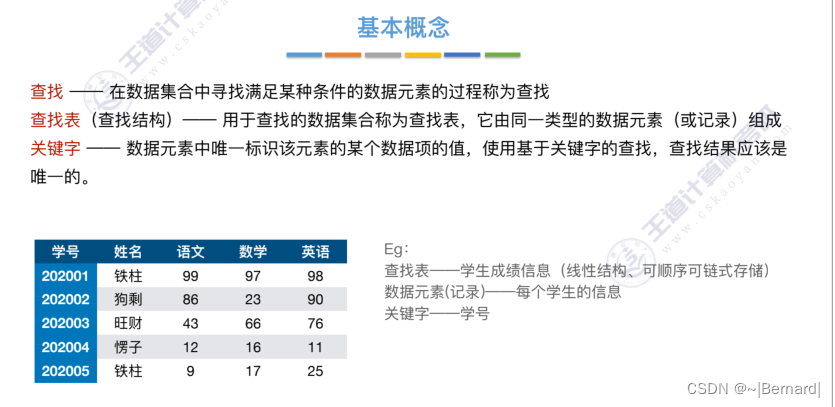
 注：查找表并不是一种新的数据结构，它只是对于你需要查找的一类数据结构的一类统称而已

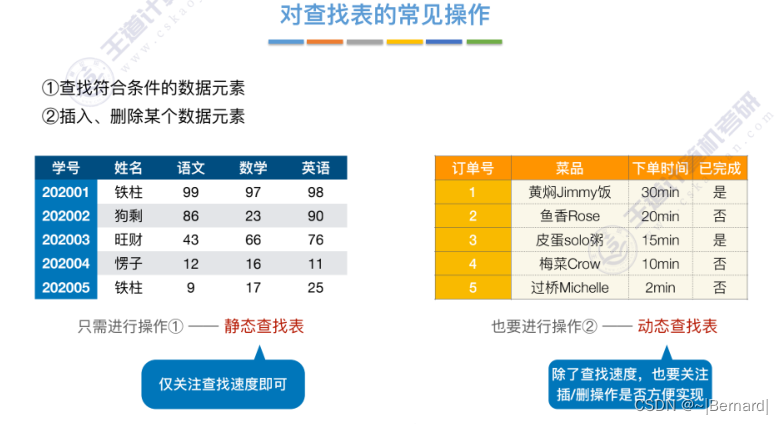
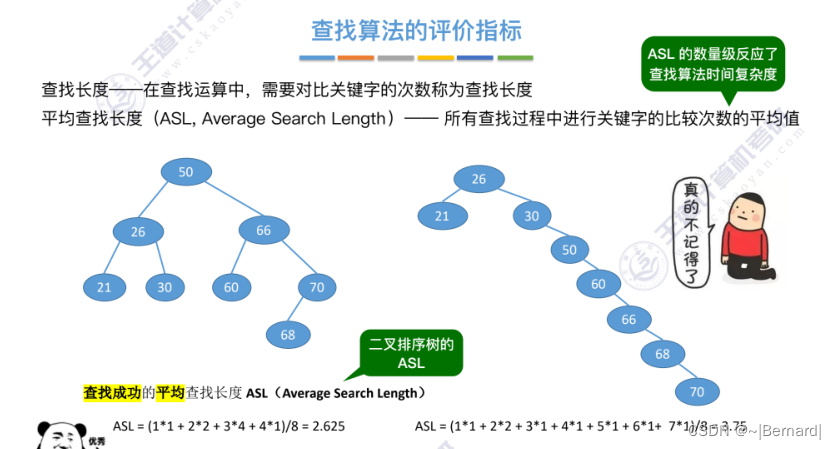
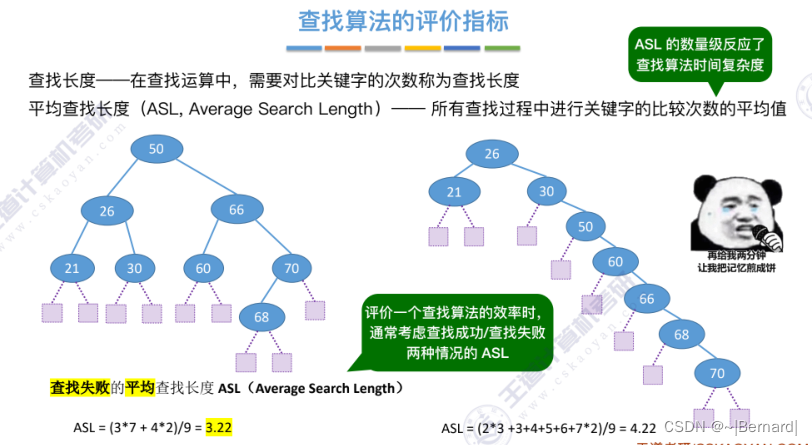
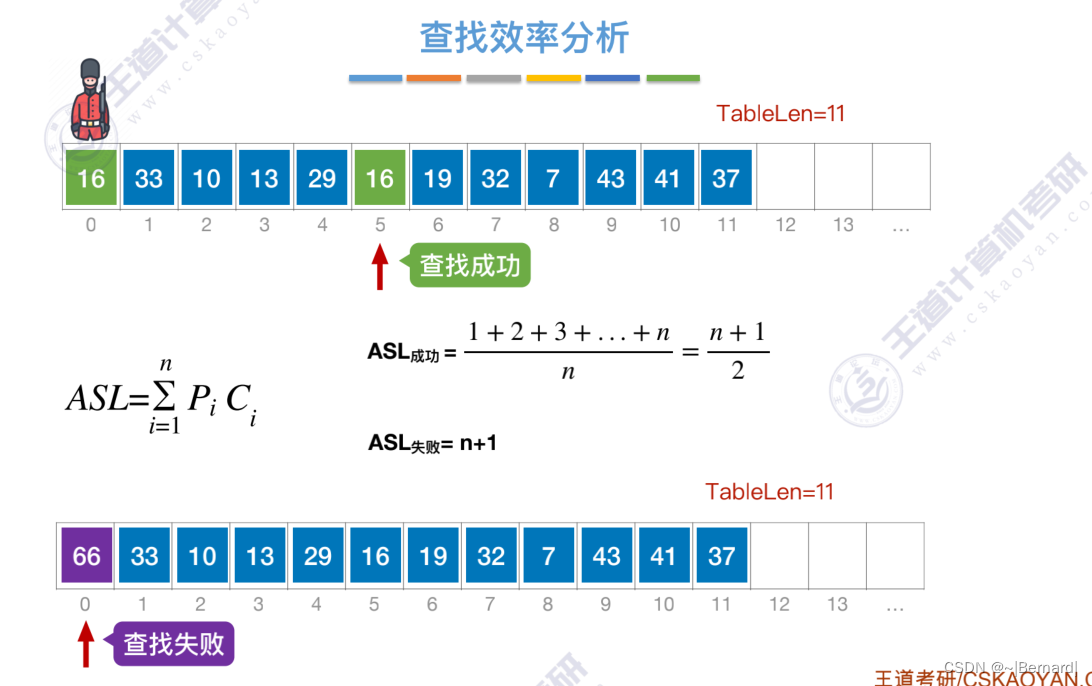
 7.2.1 顺序查找

 

 

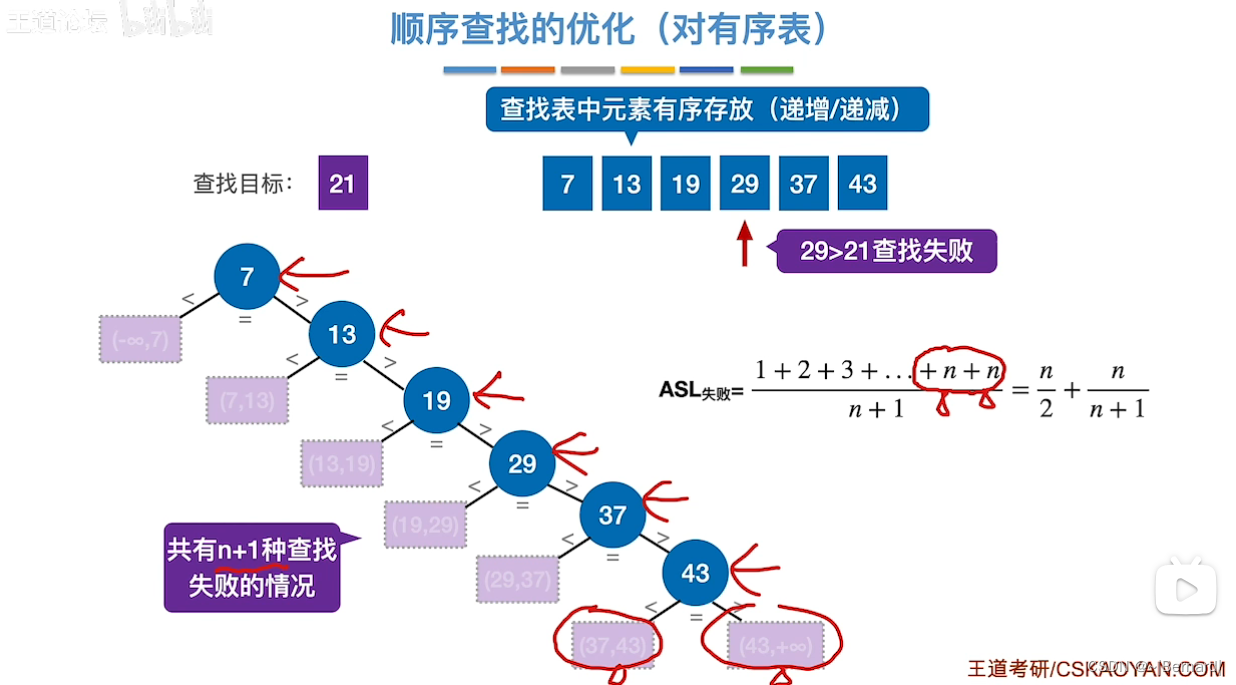
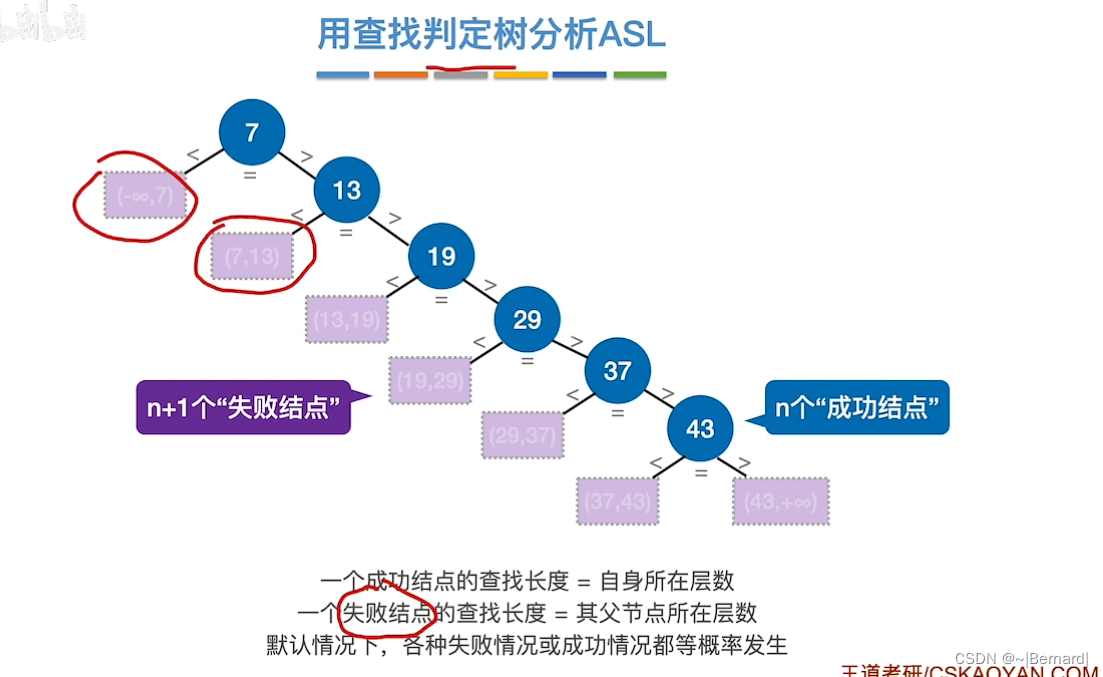
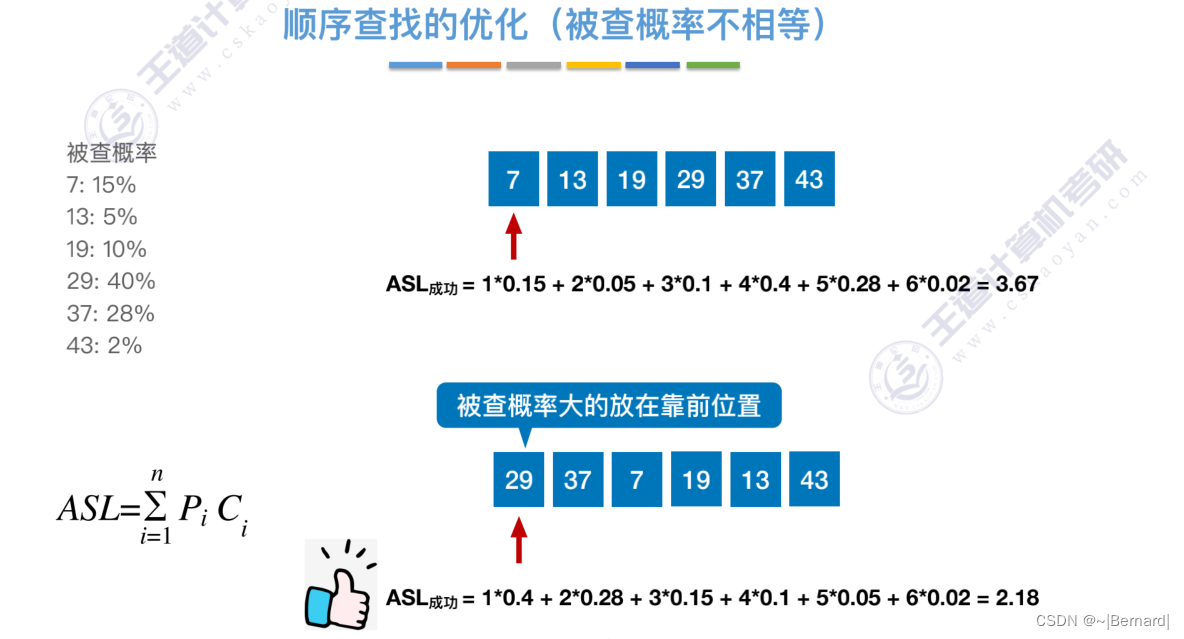
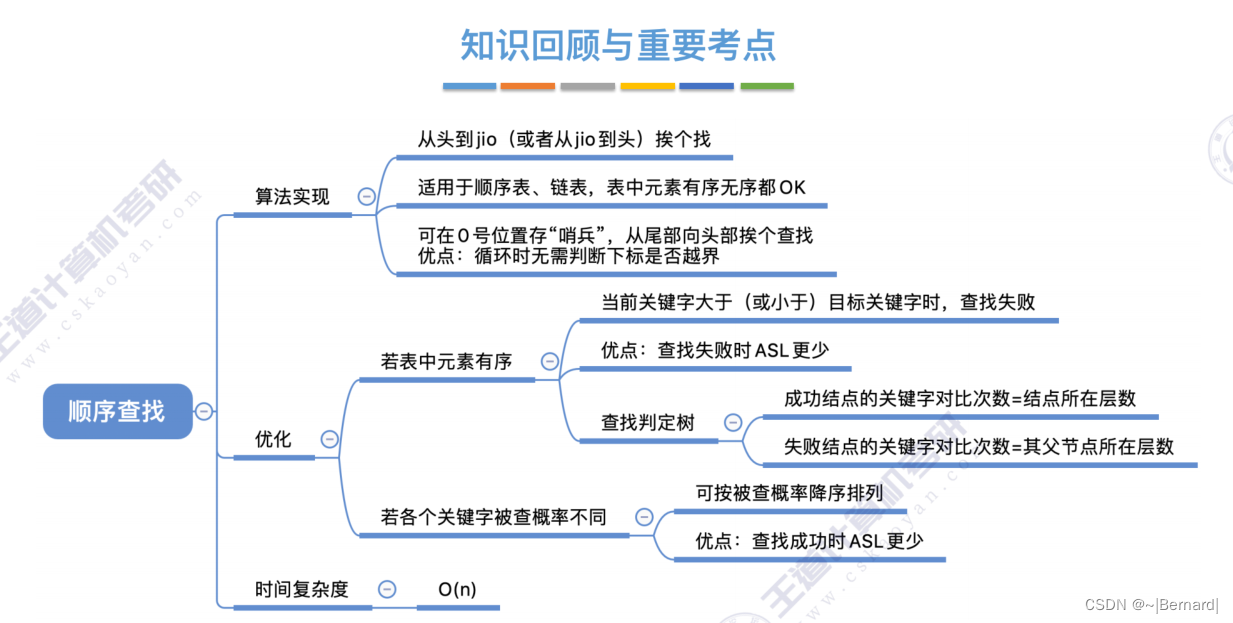
 注：学会画查找判定树 

7.2.2 折半查找(模拟算法流程详见课件)

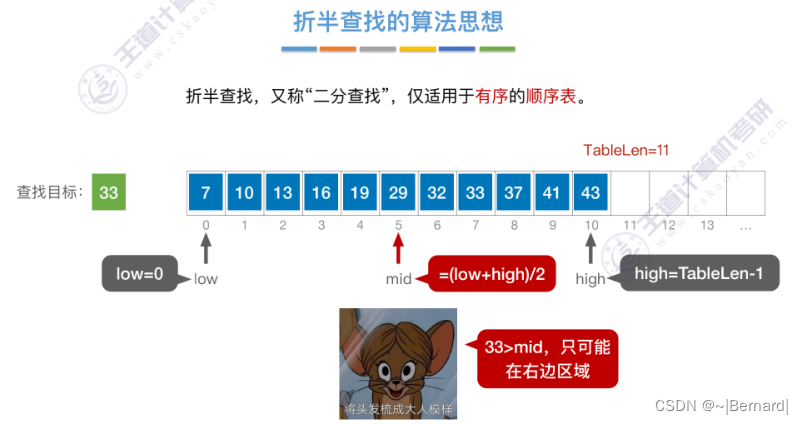
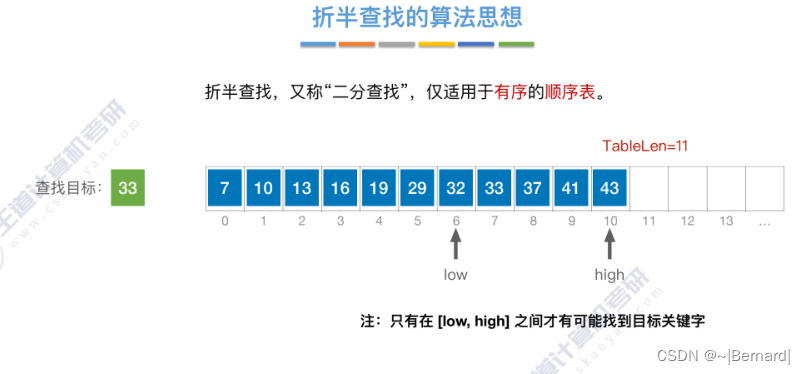
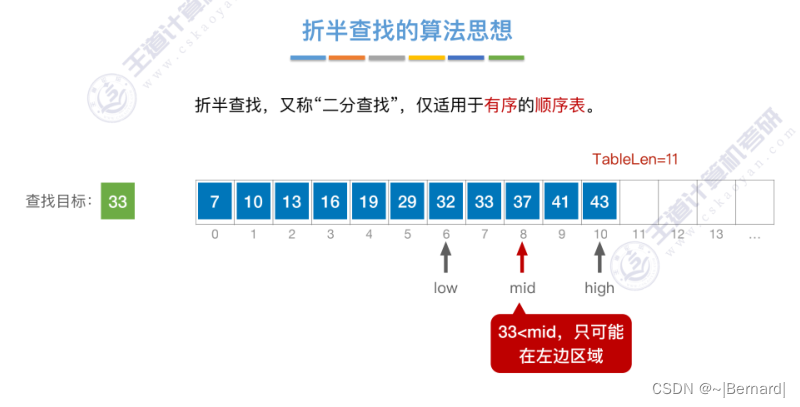
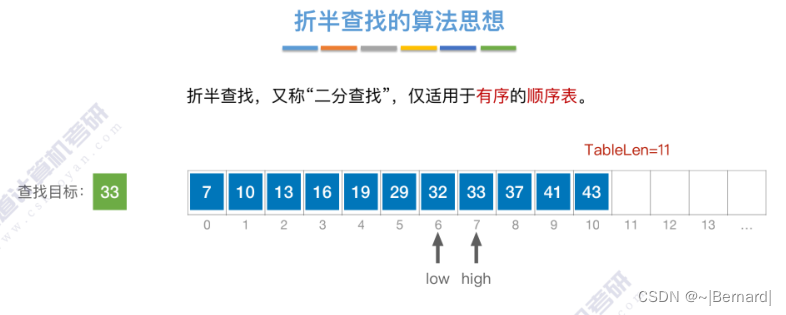 实现流程：略，见王道课件

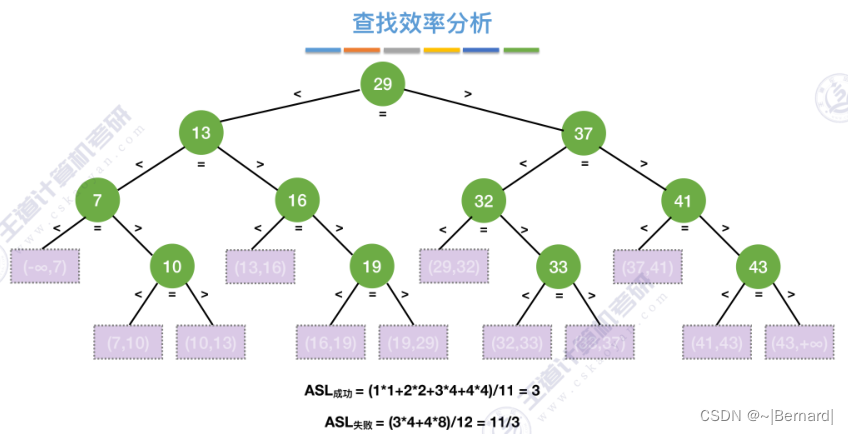
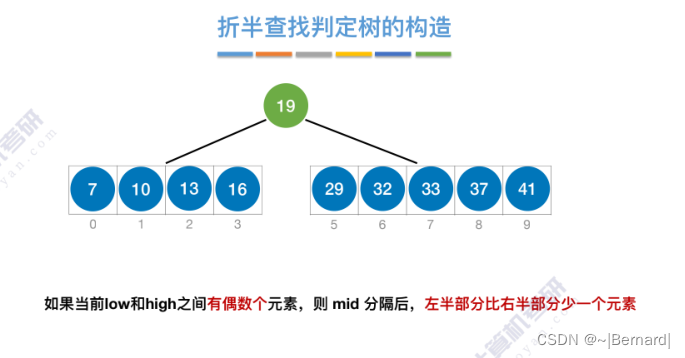
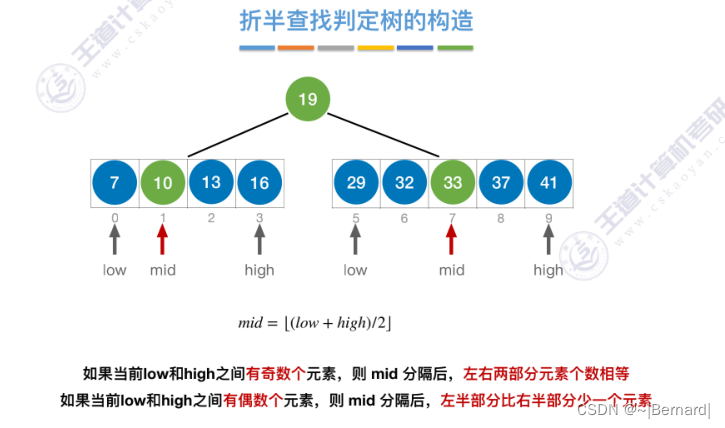
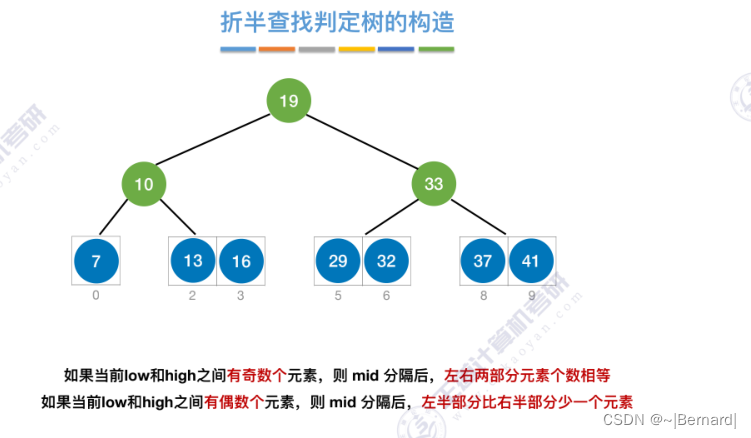
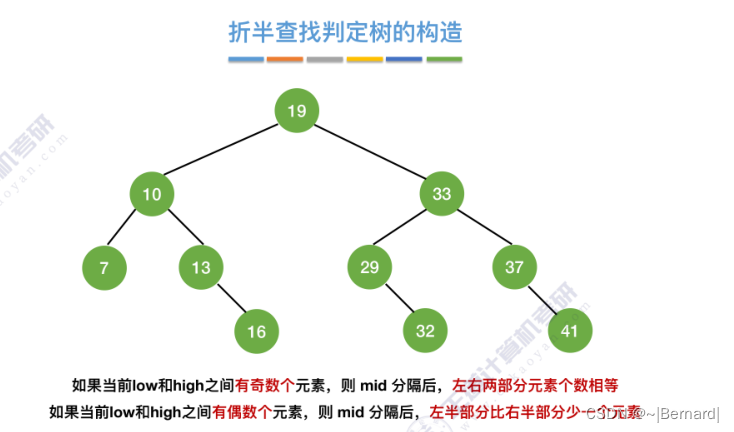
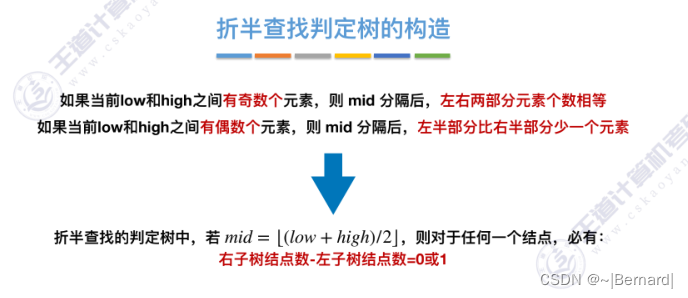
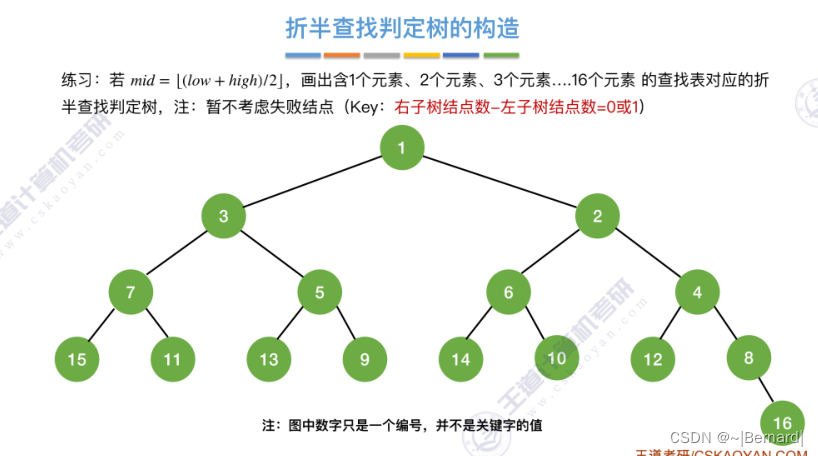
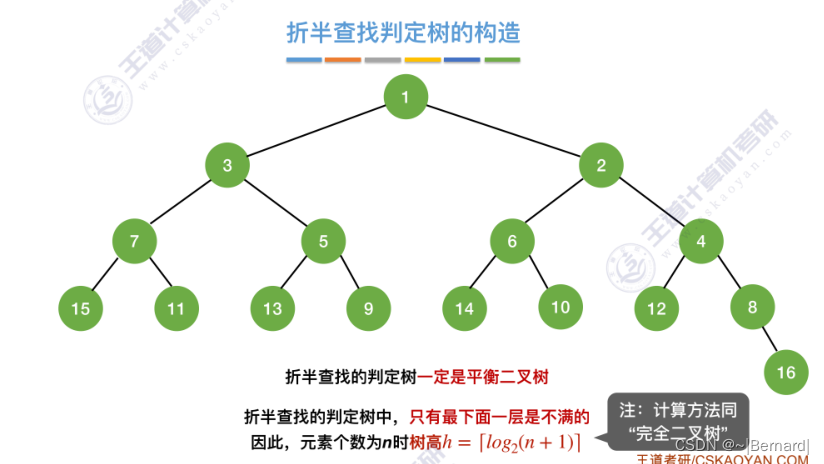
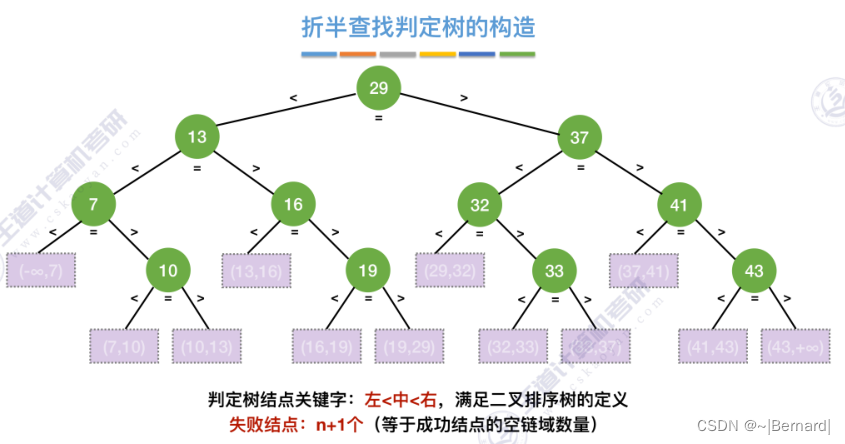
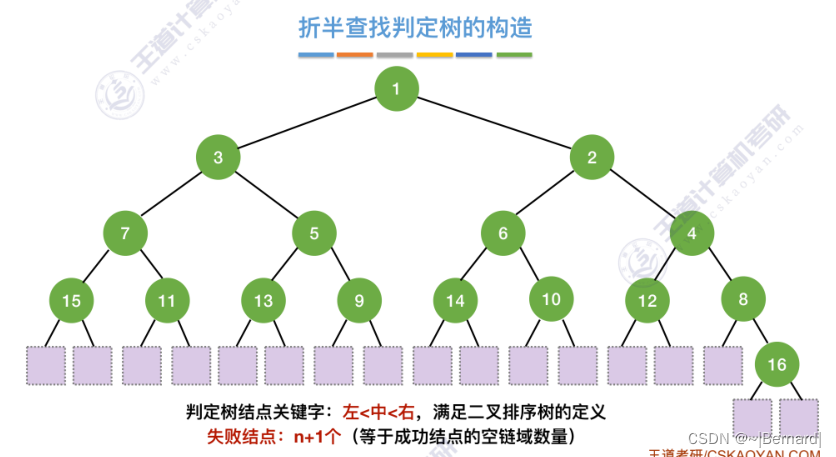
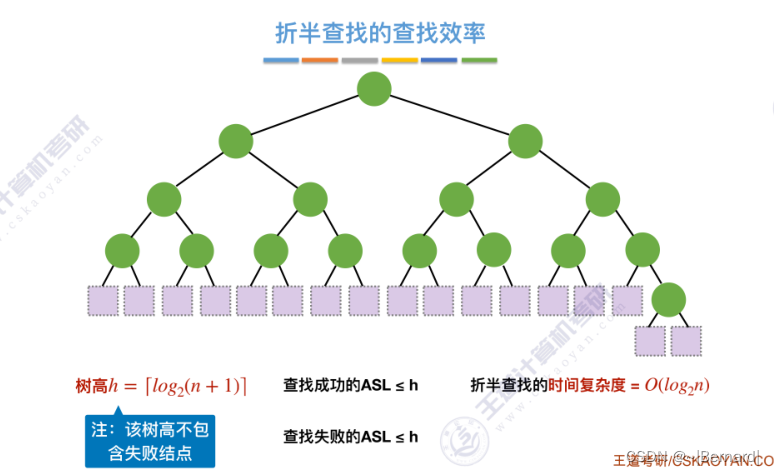
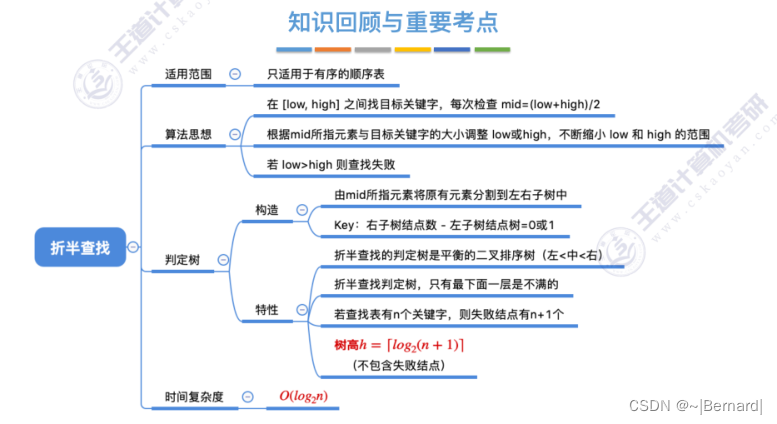
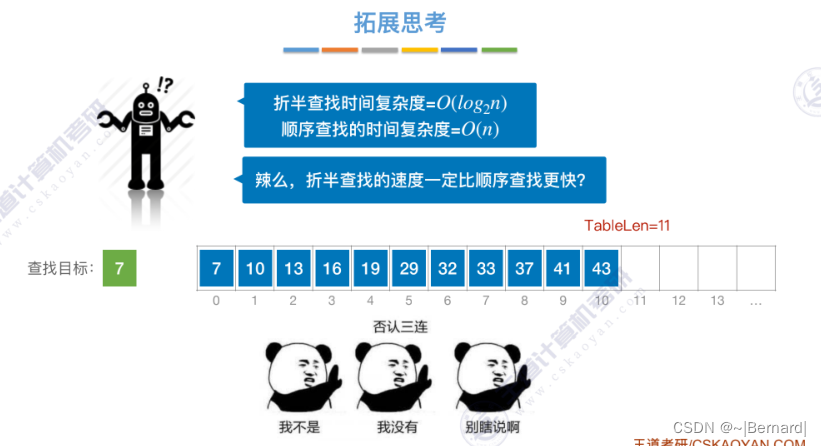
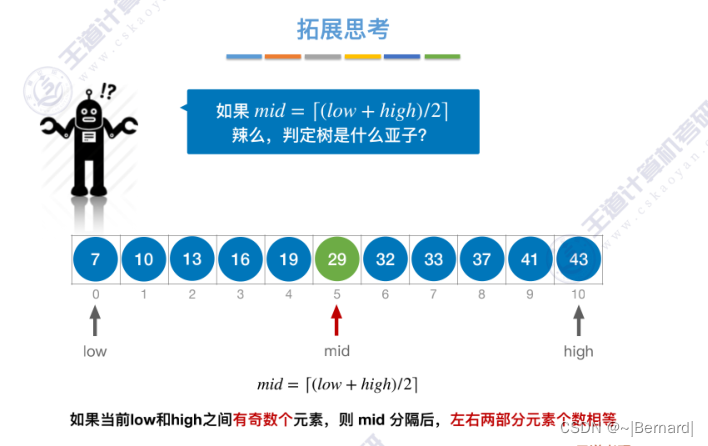
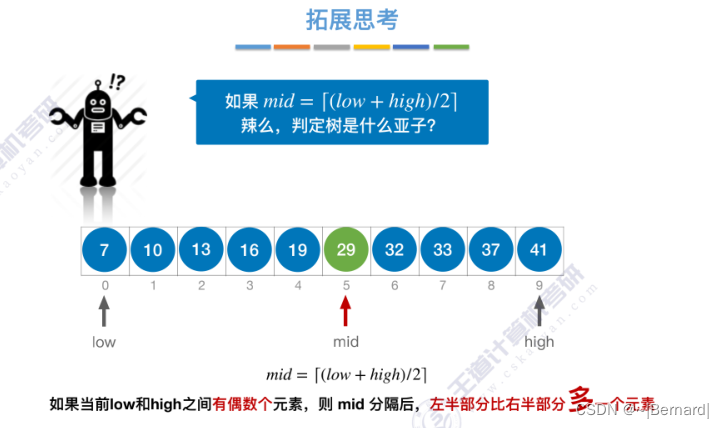
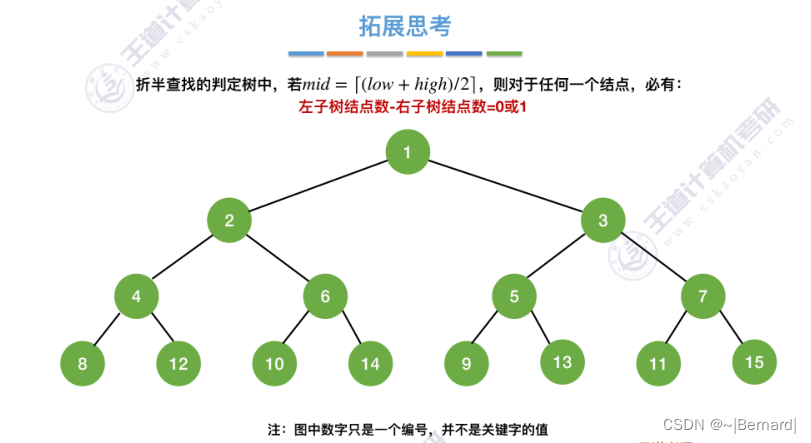
 mid如果向上取整的话什么情况？

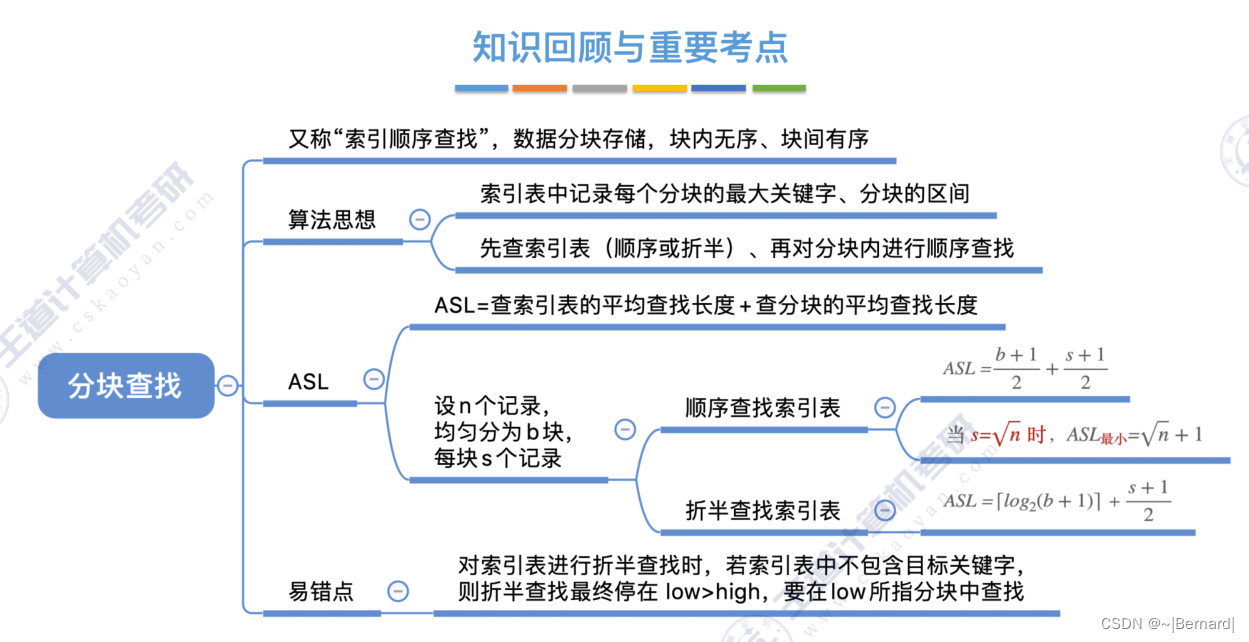
7.2.3 分块查找（模拟流程详见课件）

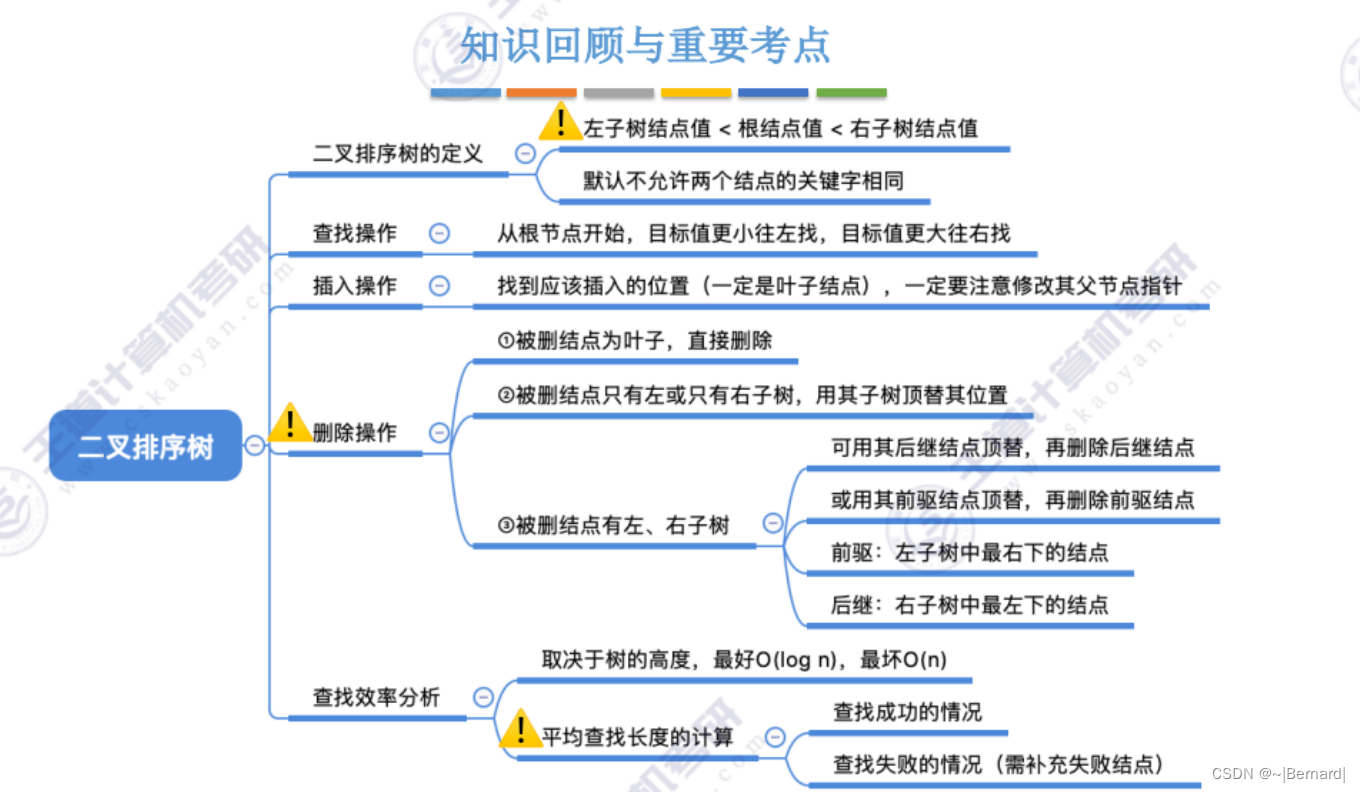
 7.3.1 二叉排序树（模拟流程详见课件）

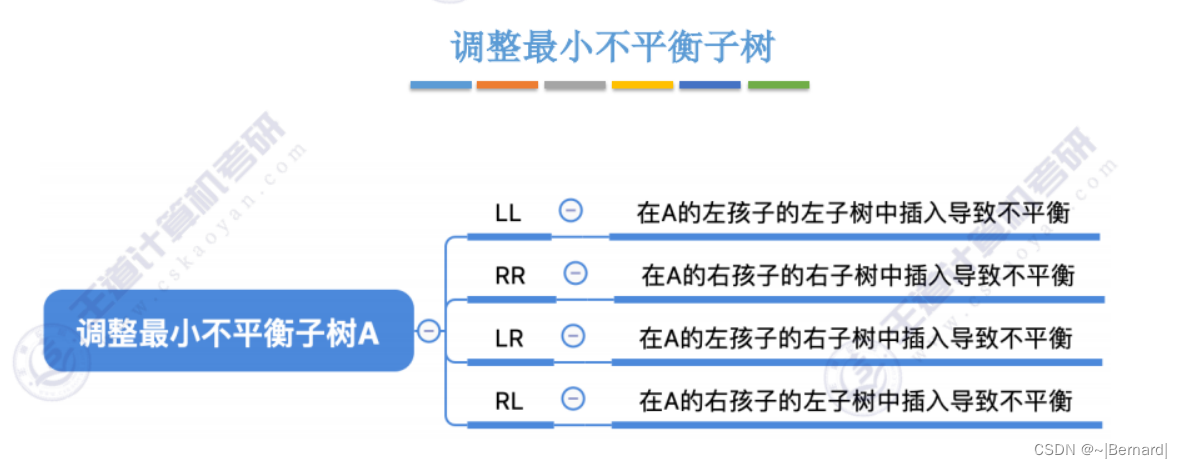
7.3.2 平衡二叉树(模拟算法流程详见课件)

注意：BST(Binary Sort Tree)是二叉排序树，AVL(Balanced Binary Tree)是平衡二叉树，不要与ASL(Average Search Length)平均查找长度混淆

为什么要假定所有子树的高度为h：为了讨论最小不平衡子树出现的情况刚好出现在A节点。

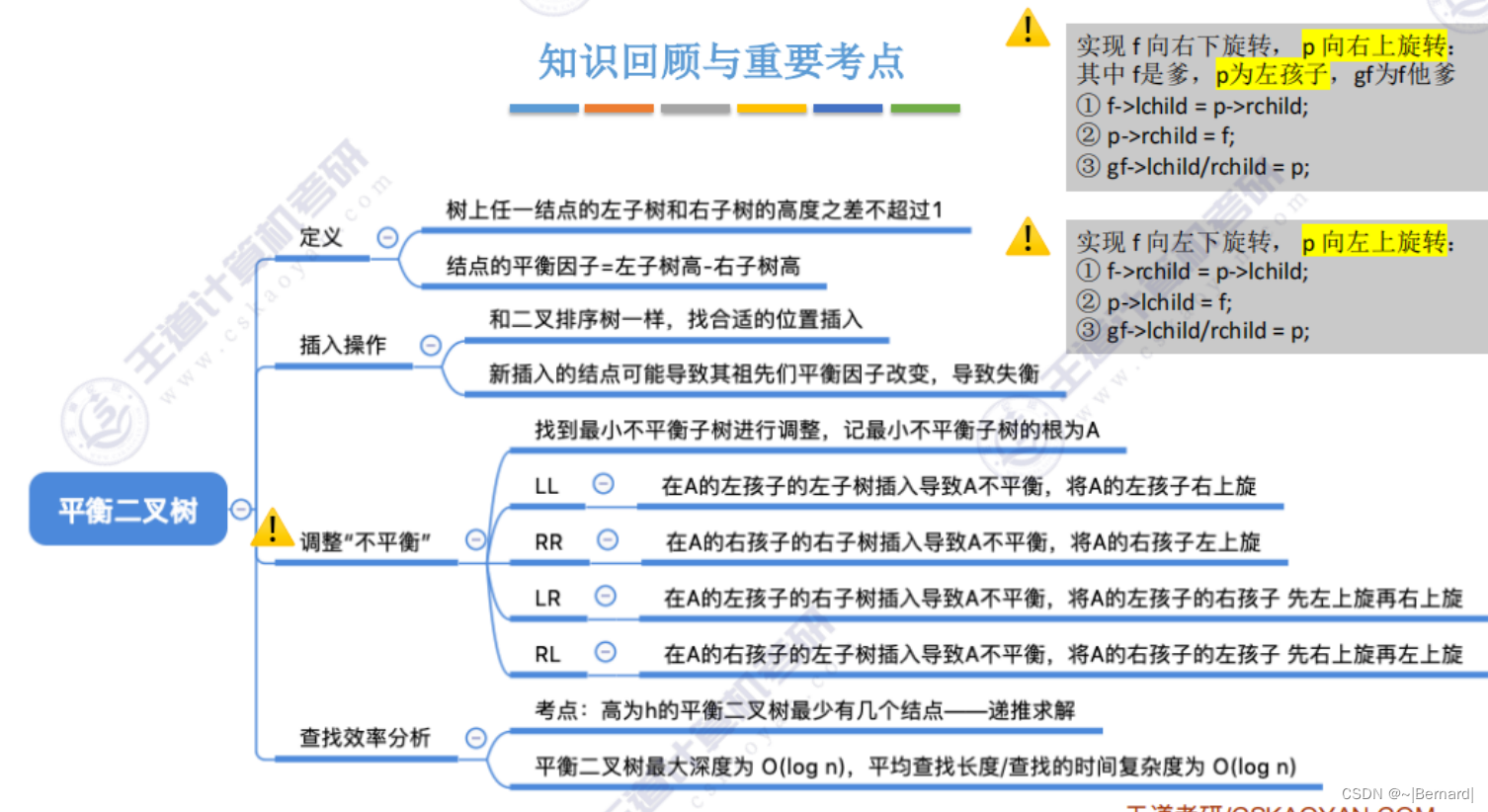
7.3.3 平衡二叉树树的删除(具体删除实例详见课件)

注：如果出现个头一样的孙子，那么选择任意一个进行旋转都可以。

注：选择前驱进行替代还是后继替代也是根据题目要求或者自身需求设定，没有强制要求。

注：删除操作和插入操作在调整树的时候都是根据孙子节点所处的位置进行调整的。

 

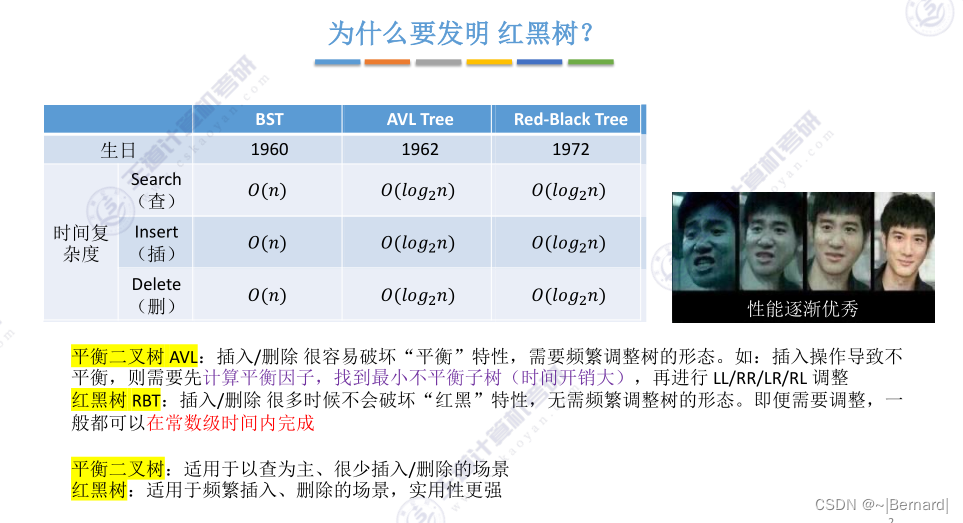
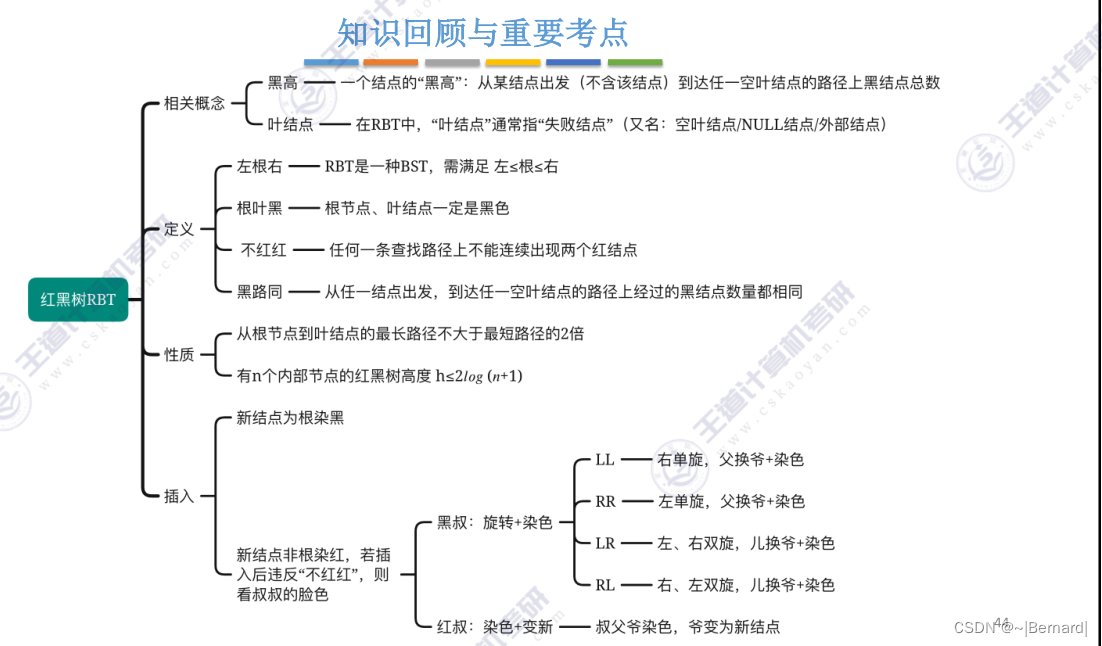
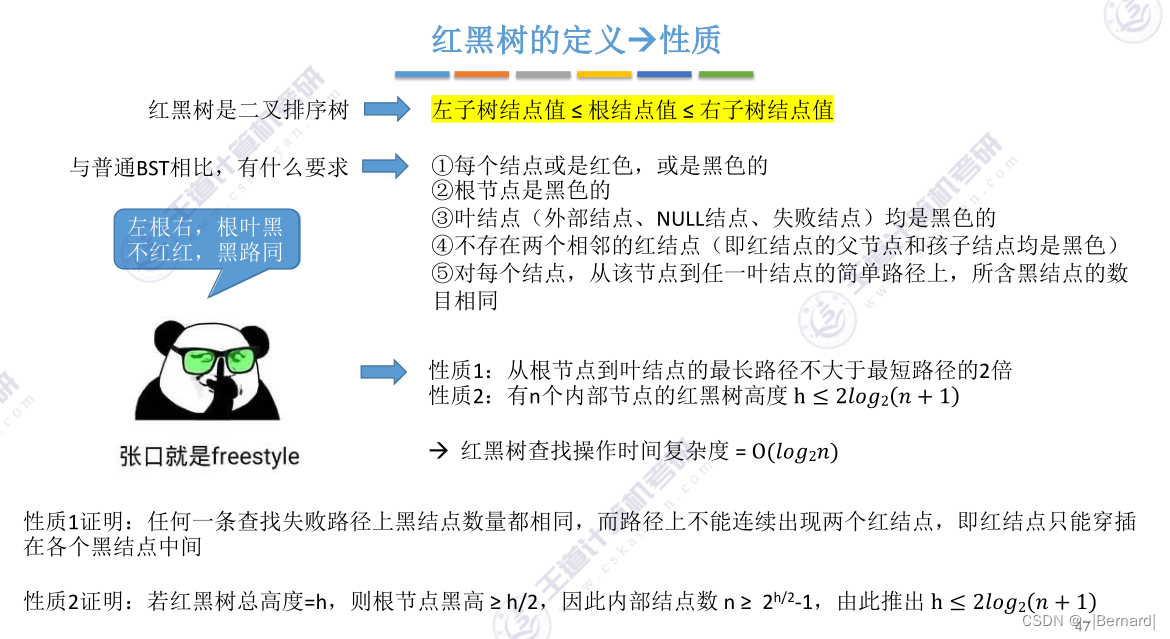
 7.3.4 红黑树RBT(Red-black Tree)的定义和性质（详见课件）

注意：红黑树中的叶节点指的并不是最下层的节点，而是NUll节点

红黑树口诀：

1.左根右(左子树＜根 < 右子树)

2.根叶黑(根节点，叶节点必须是黑色的)

3.不红红(不存在两个相连的红节点)

4.黑路同(任意节点出发，走到叶节点经历的黑节点数目一定是相同的)

 

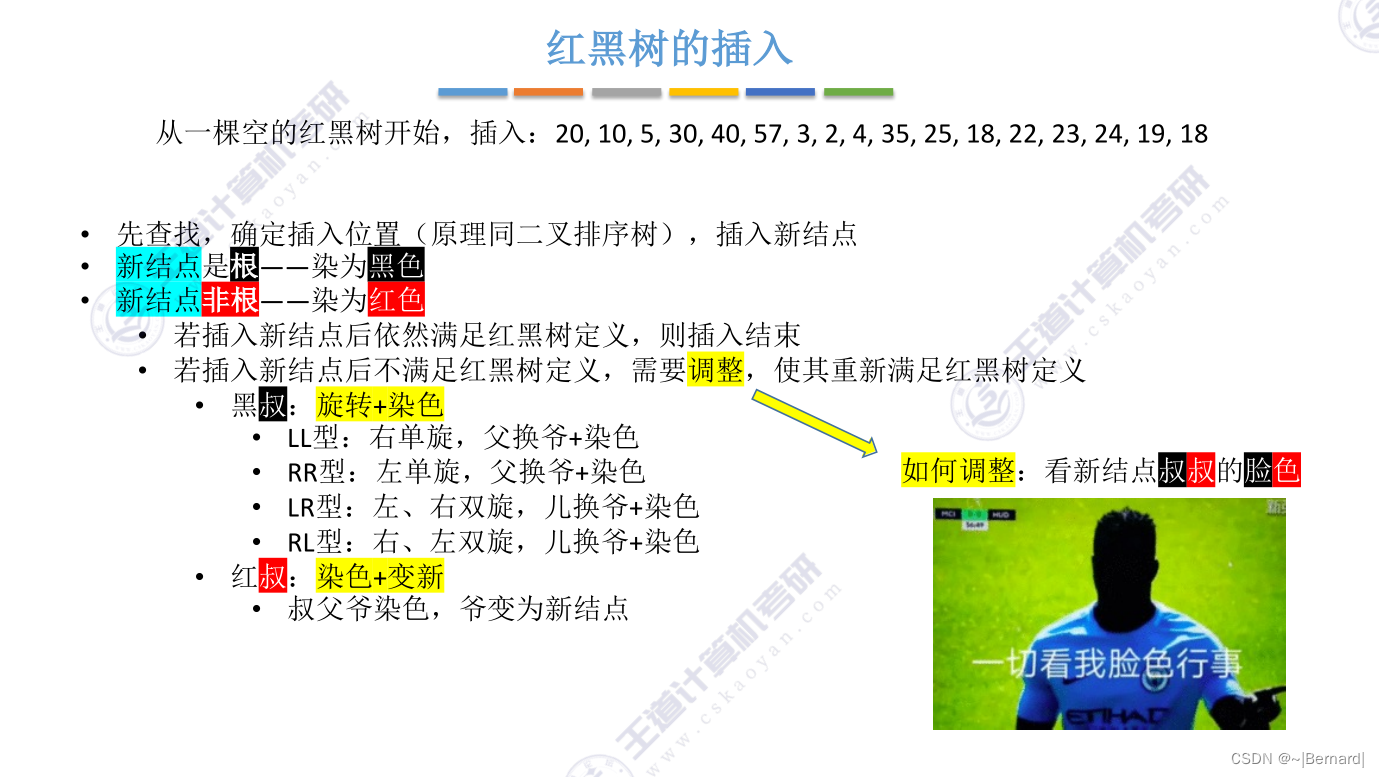
 7.3.5 红黑树的插入(详见课件)

注：为什么插入非根节点的时候我们要先染红色呢？这么做的原因是要保证黑路同的特性，如果刚开始涂成黑色就会导致新插入节点的路径黑节点多一个，不满足红黑树的定义。

注：判断属于什么类型是从爷节点开始判断的。

注：黑叔中染色：交换的节点原本是红的变为黑的，原本是黑的变为红的。

注：红叔中染色：原本的爷节点视为新节点，是为了如果不是新节点需要继续向上迭代处理，如果是根节点则染为黑色。

注：插入一个新节点之后，破坏的都是不红红这一特性。

注：最后一个18这里规定往后边走

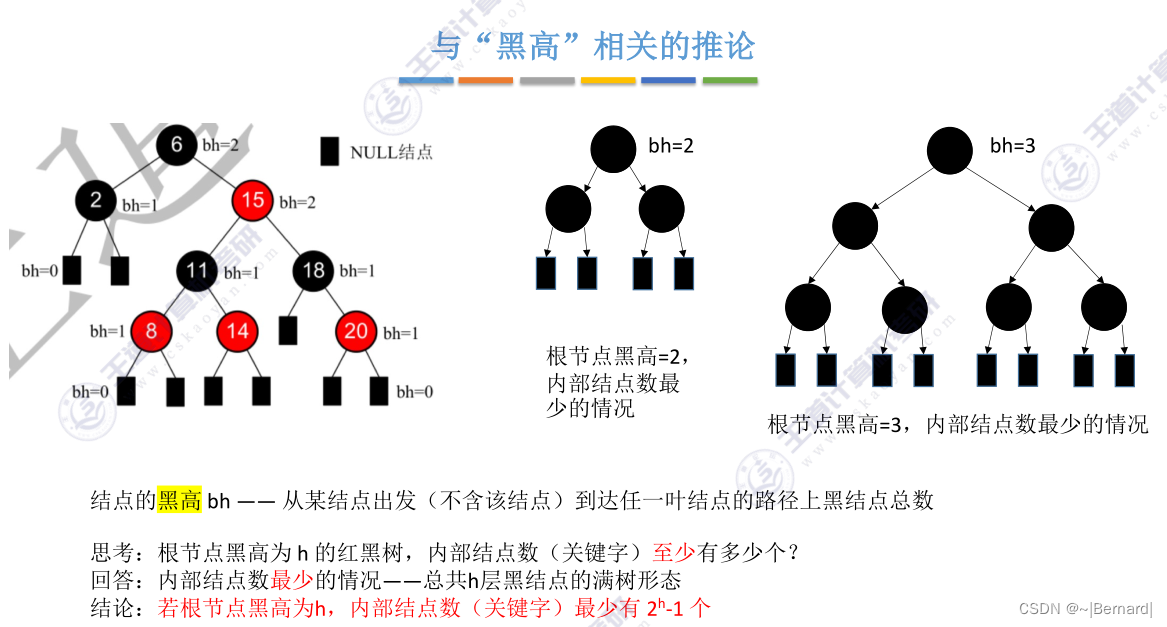
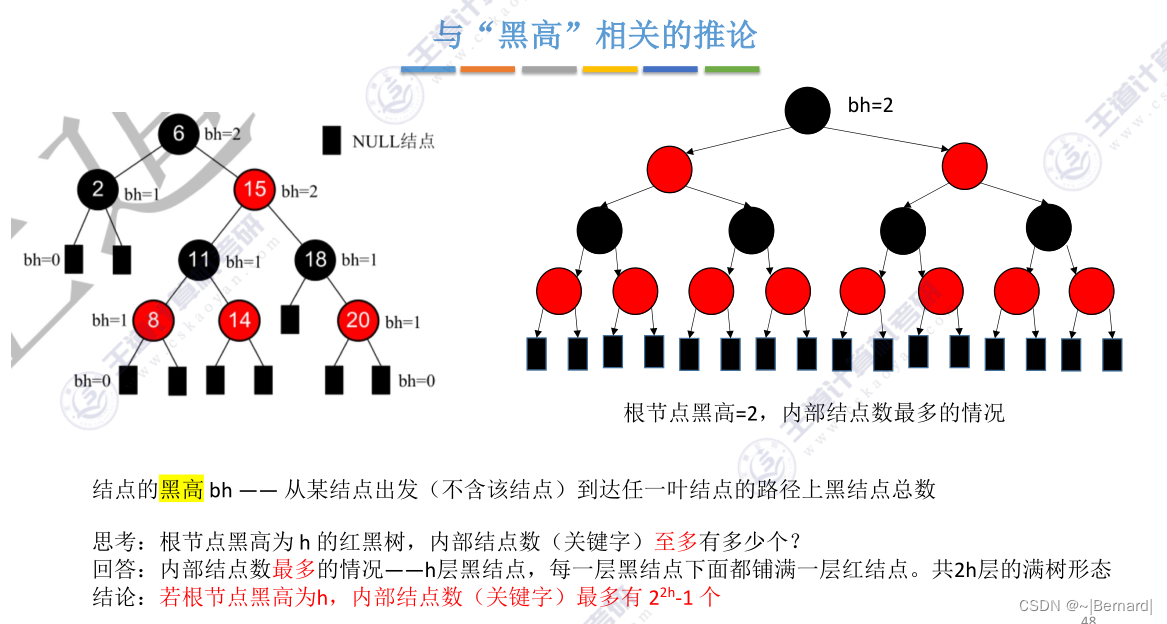
注：内部节点数(带关键字的节点)，不包含外部节点(即NULL节点)

 

 7.3.6 红黑树的删除

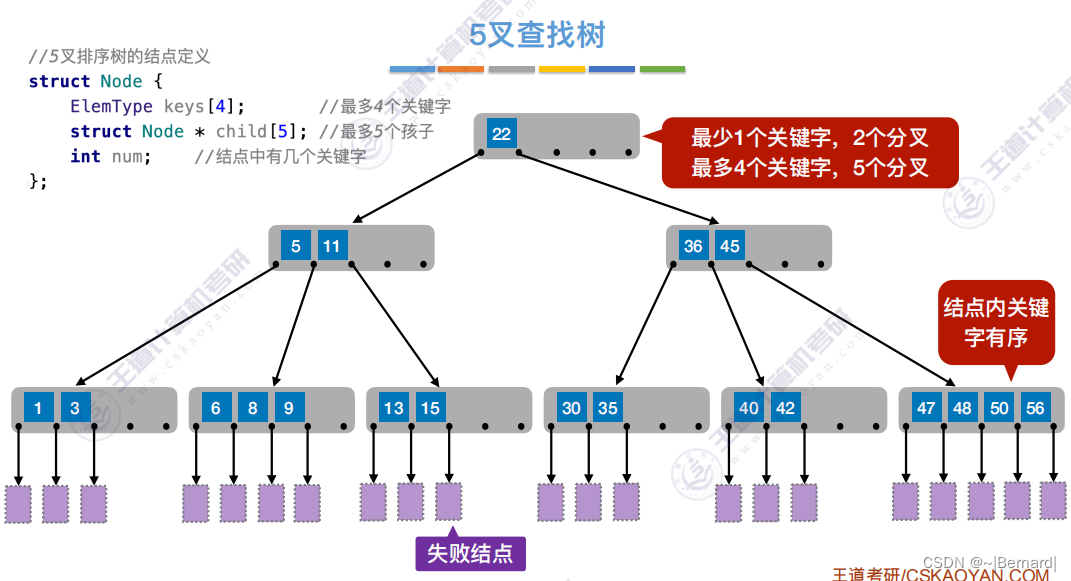
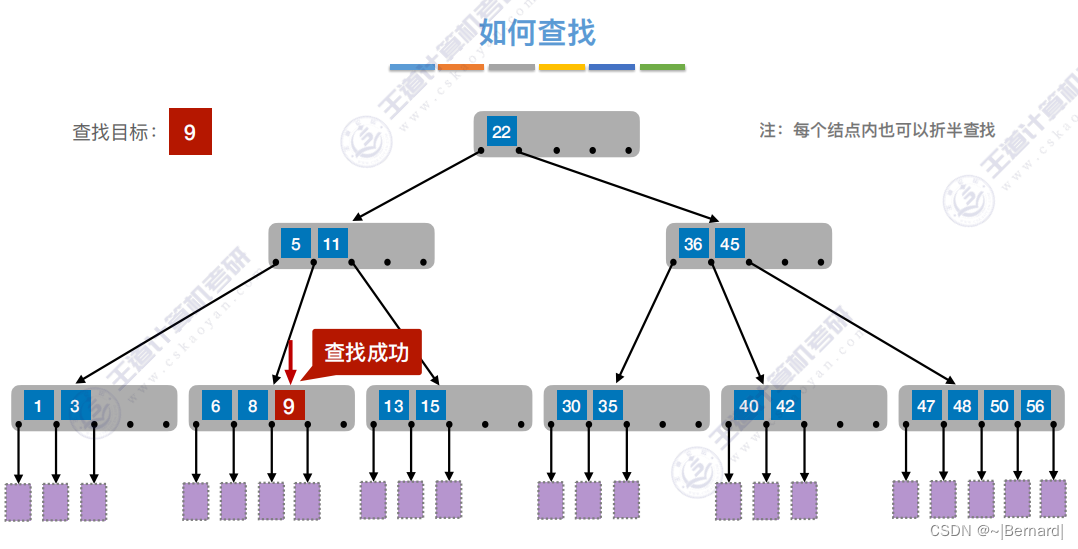
7.4.1 B树

 

 

 

 

 

 

 

 

 

 

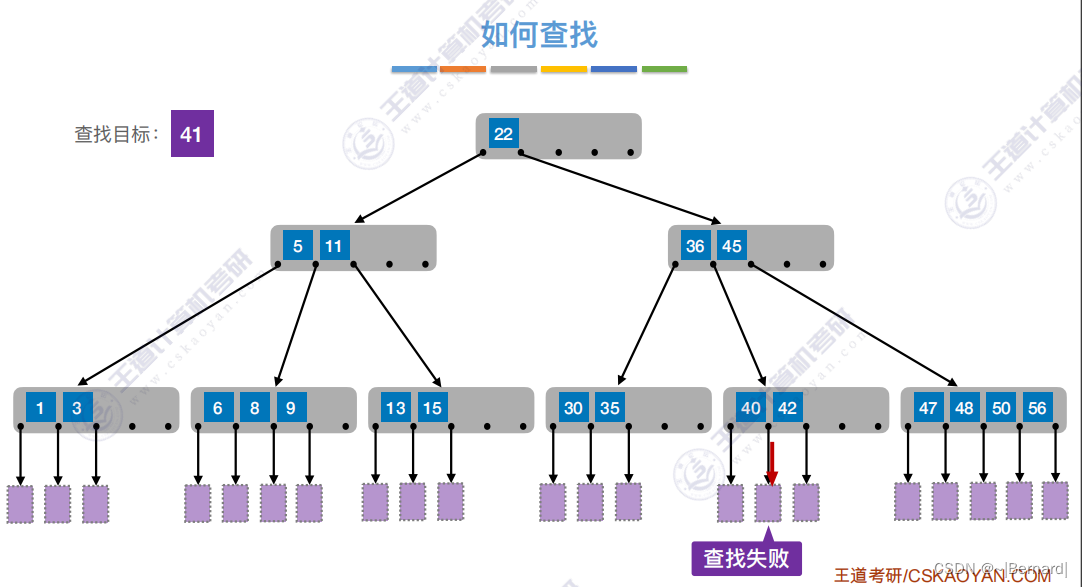
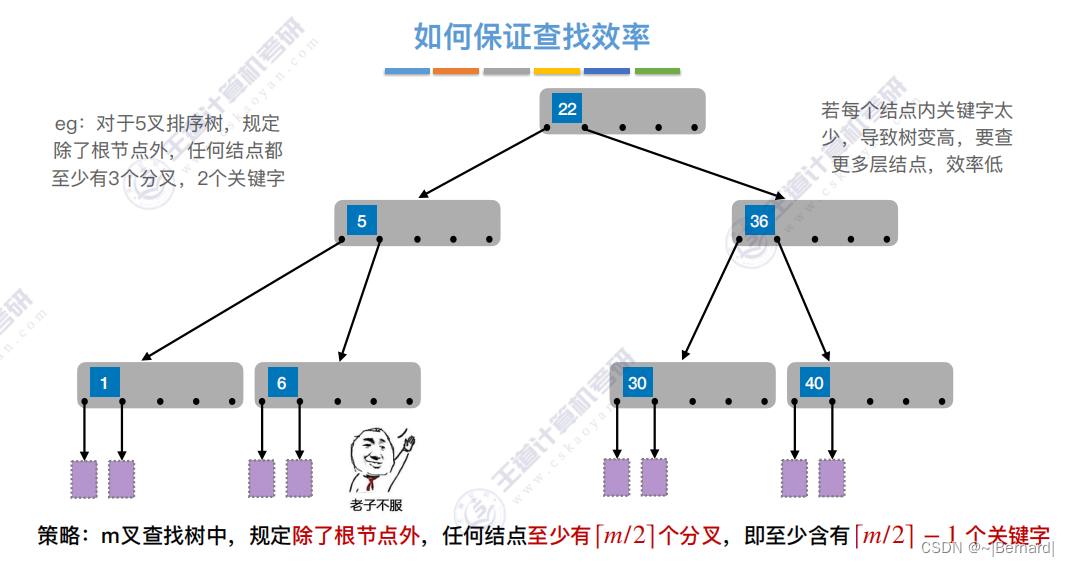
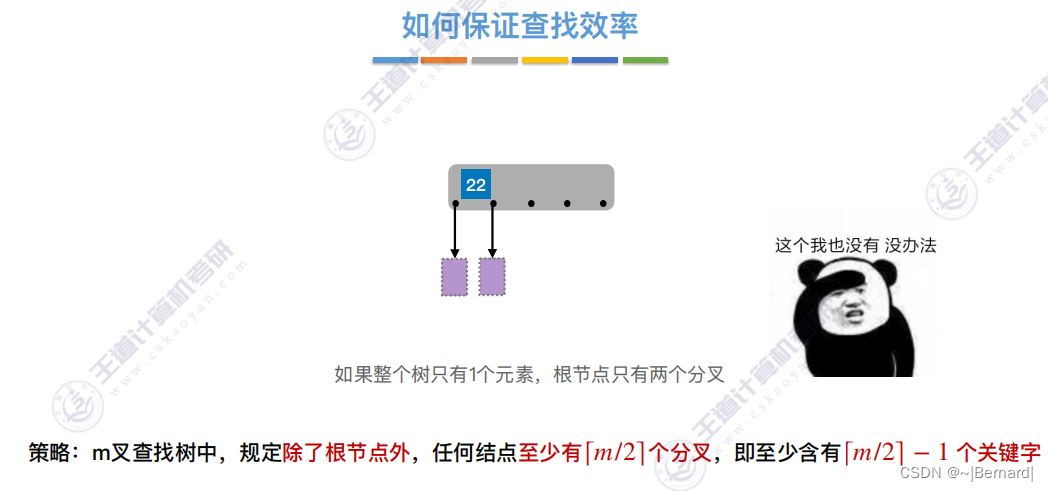
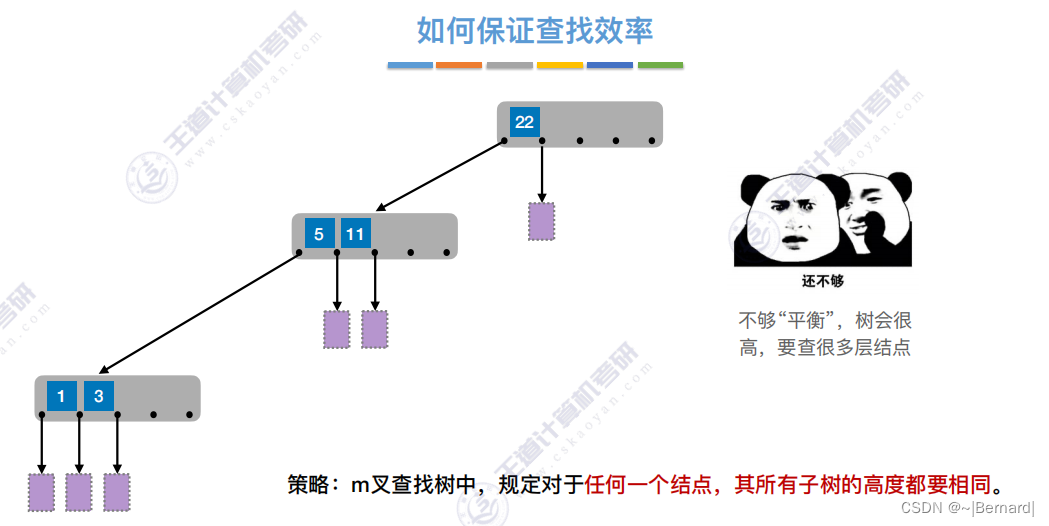
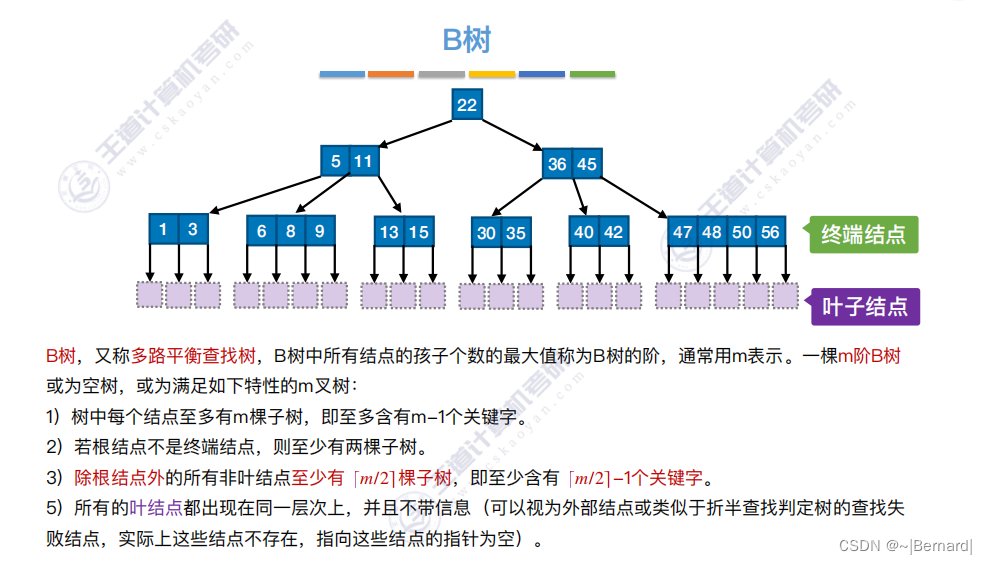
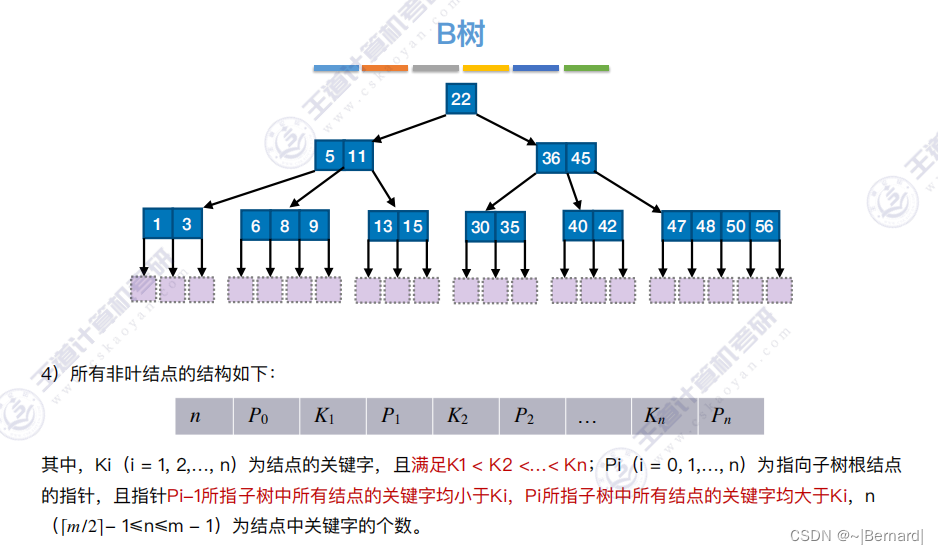
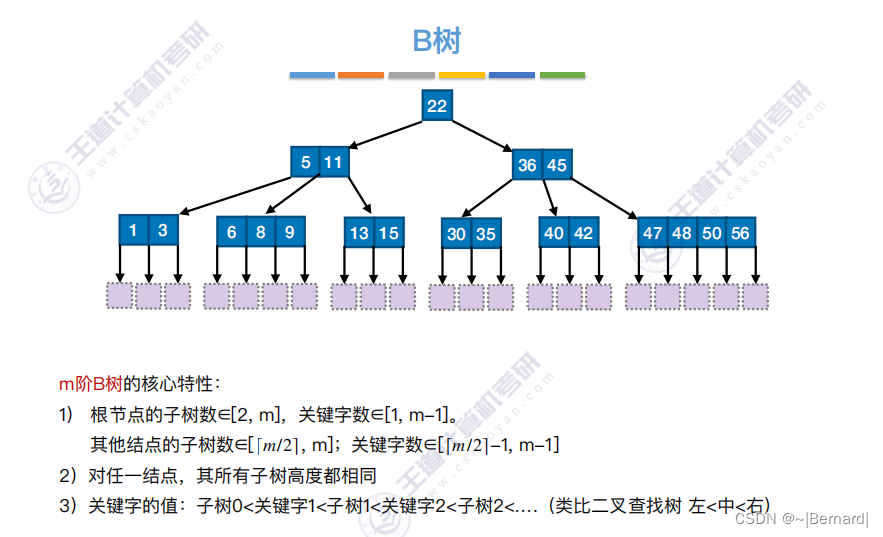
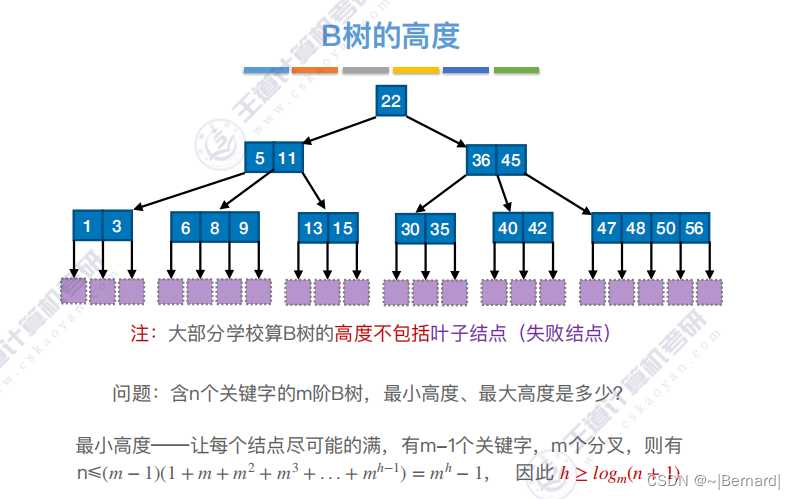
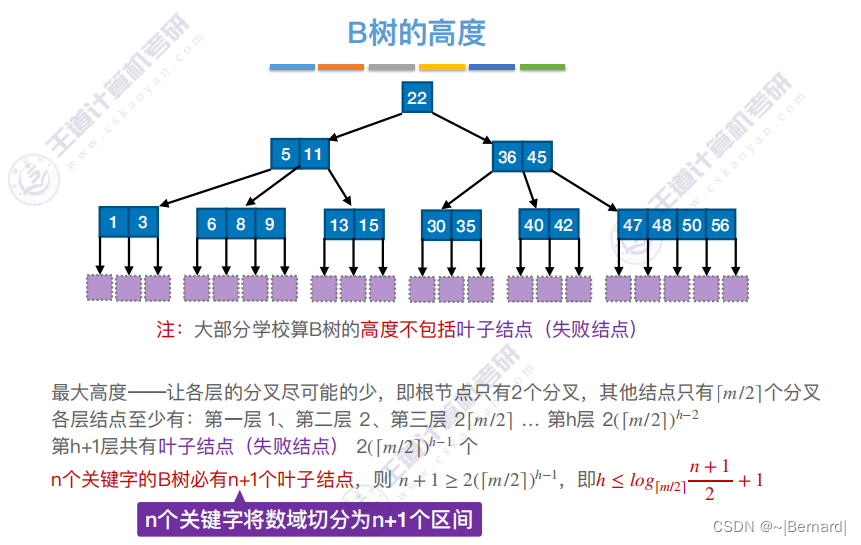
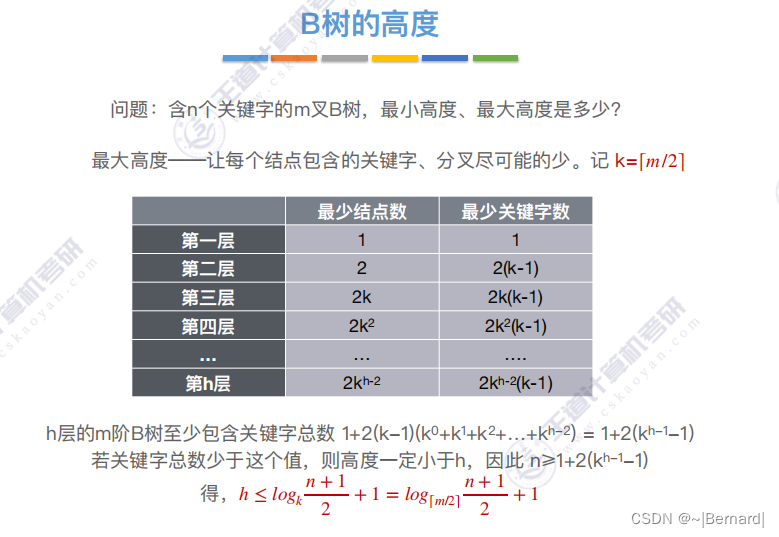
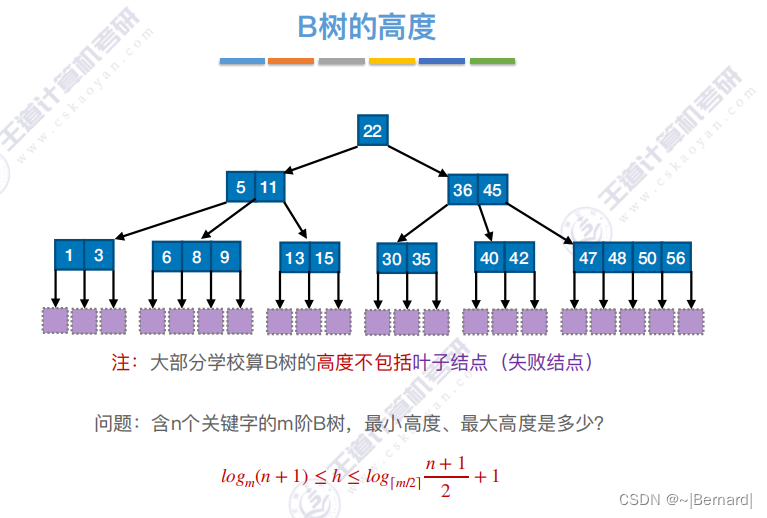
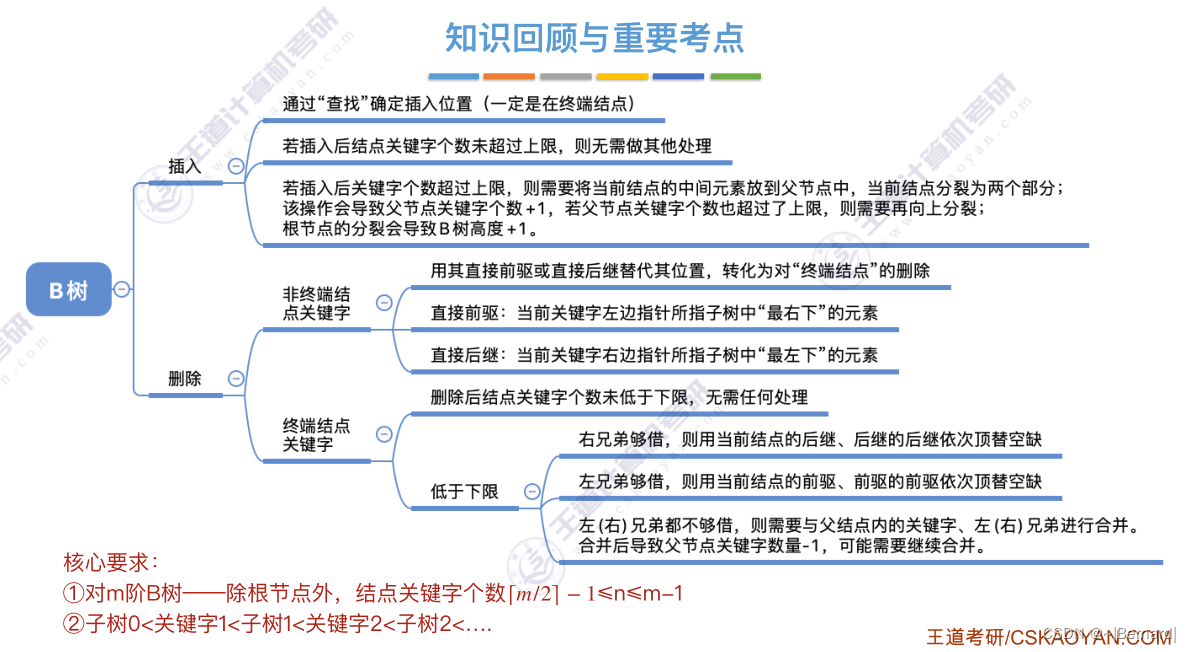
 7.4.2 B树的插入和删除(详见课件)

7.4.3 B+树

 

 

 

 

 

 

 

 

 

 

 

 

 

 

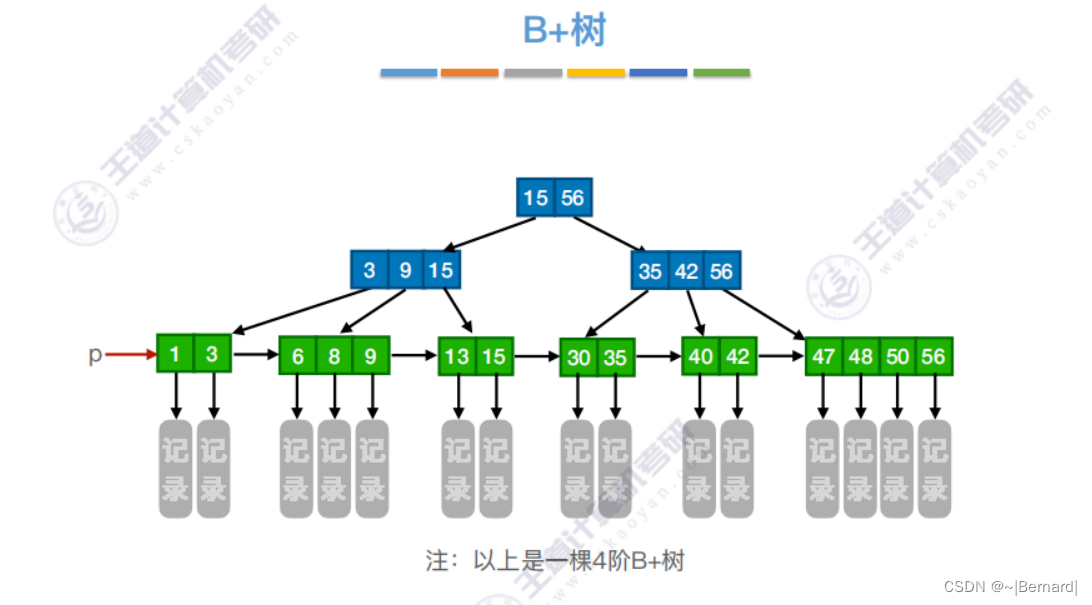
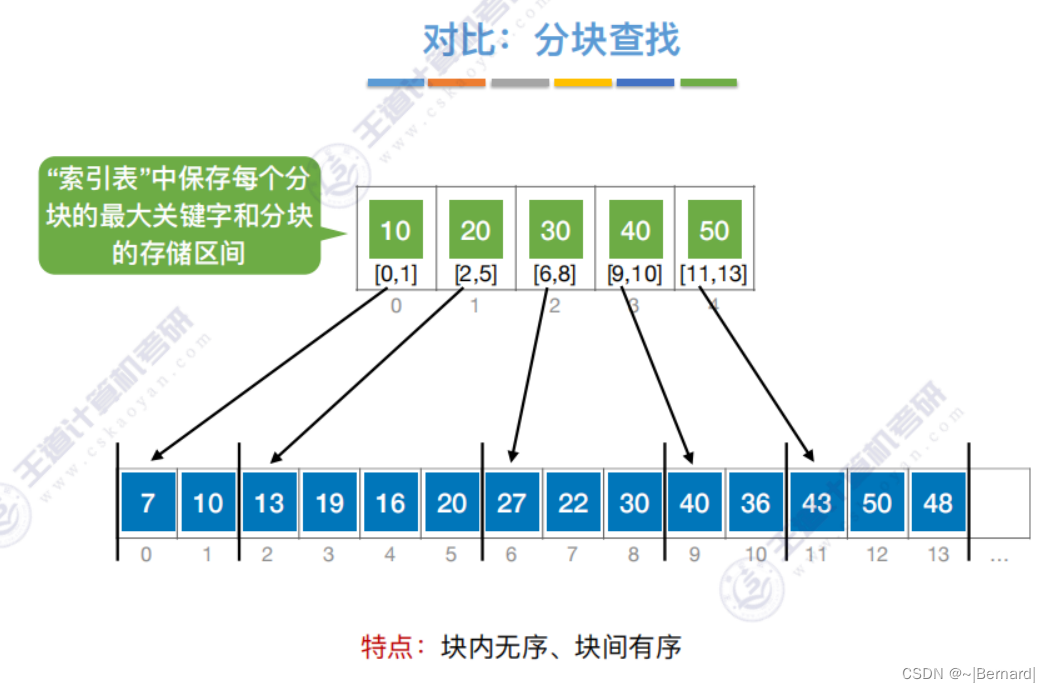
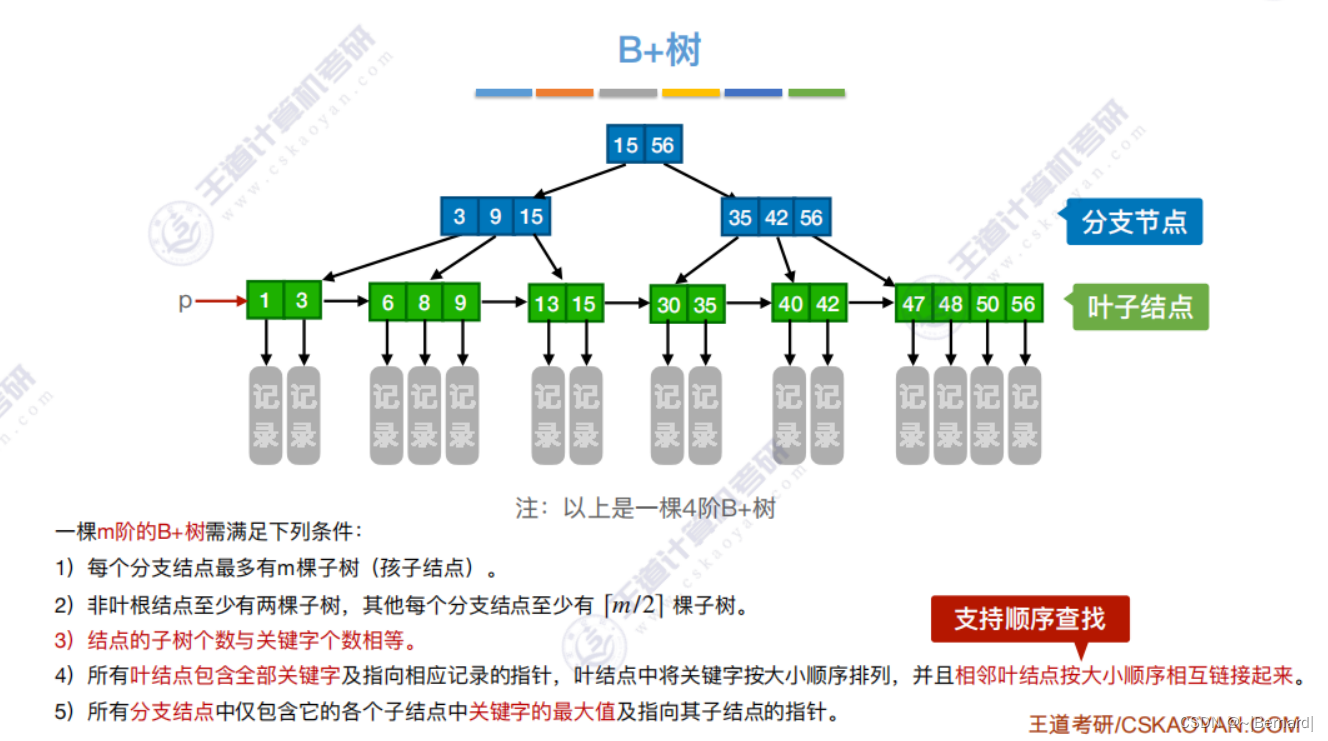
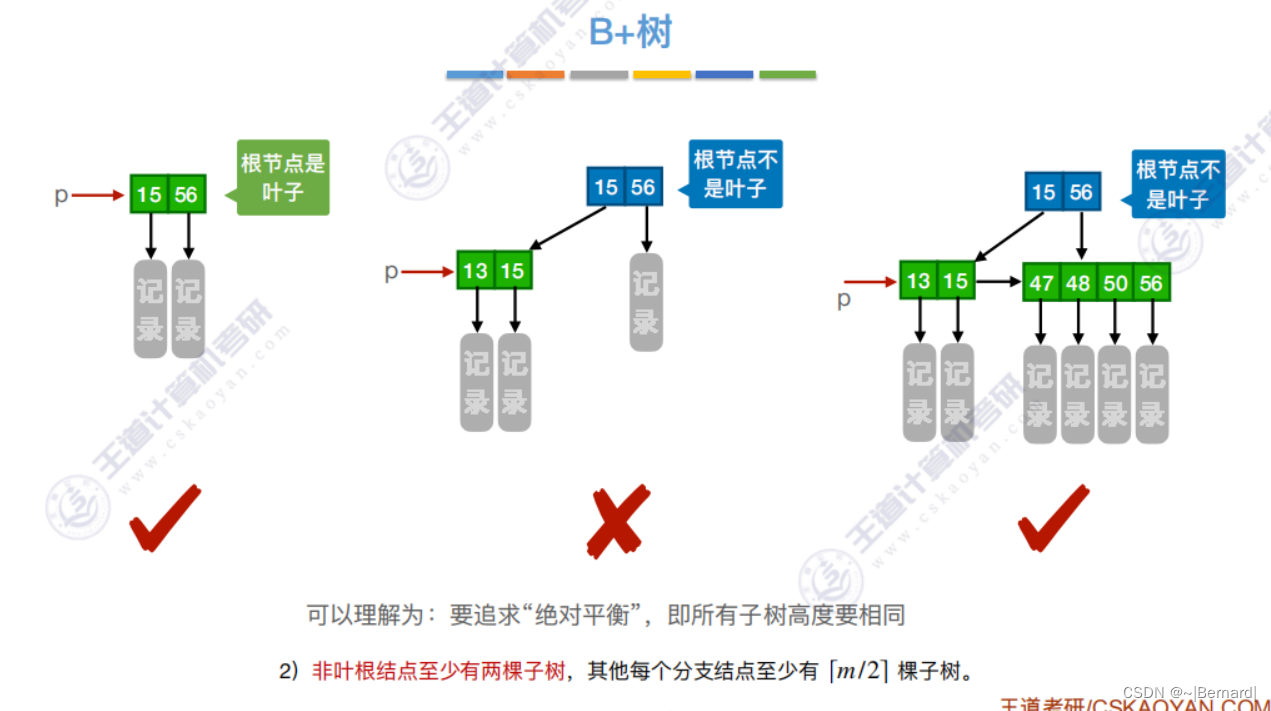
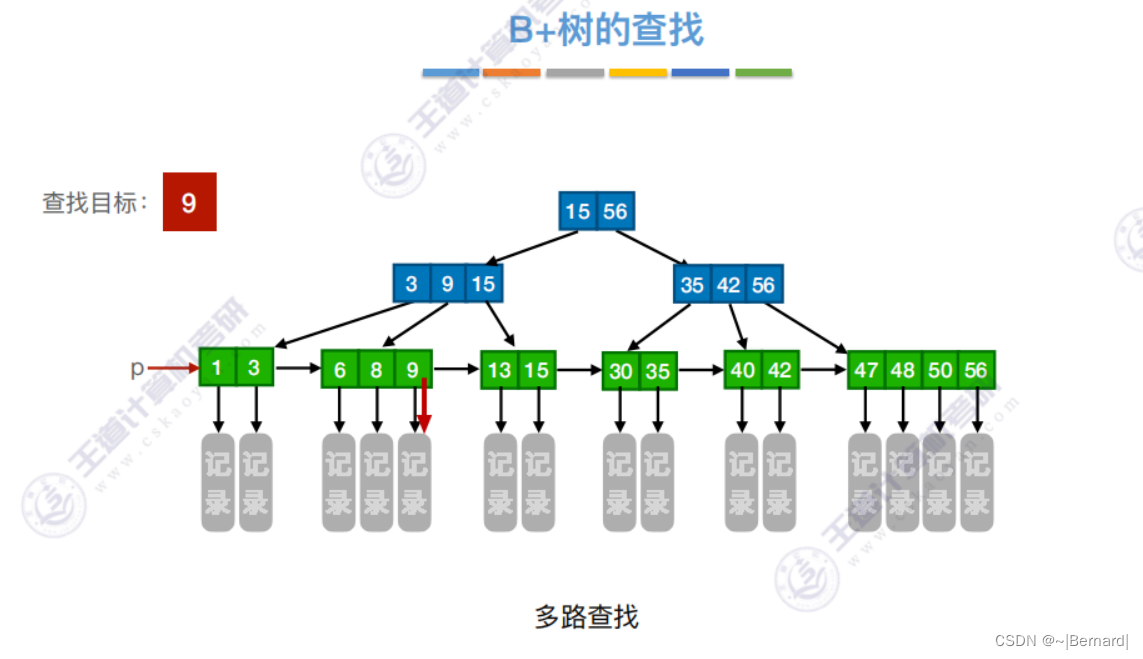
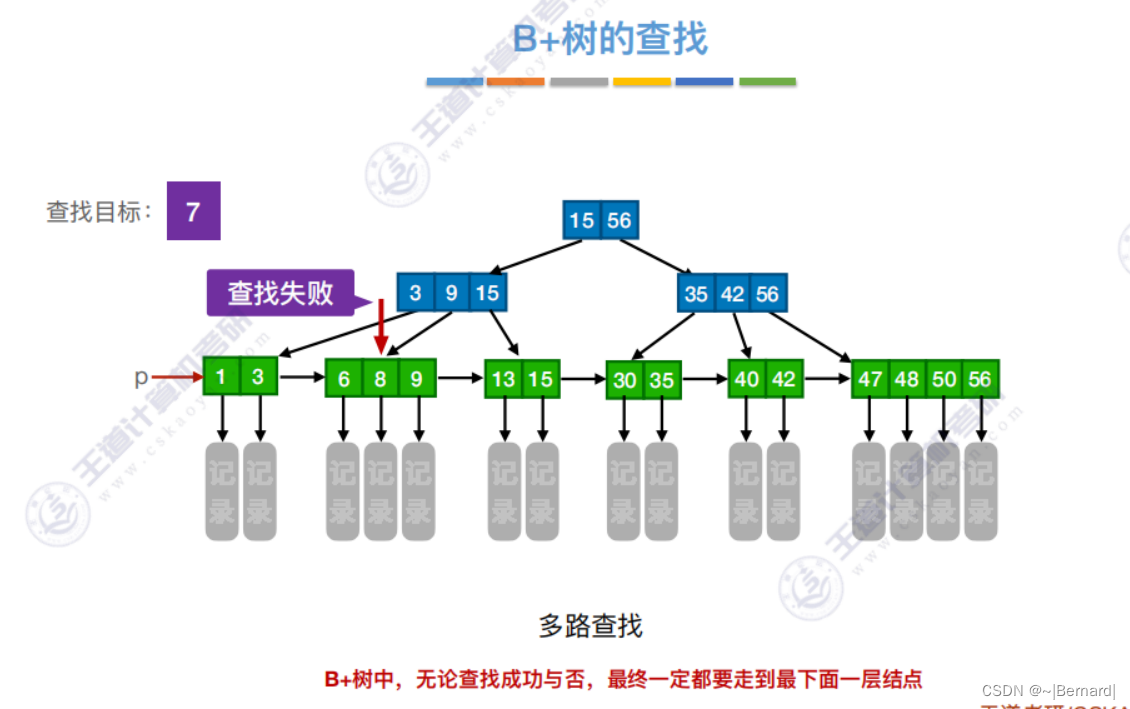
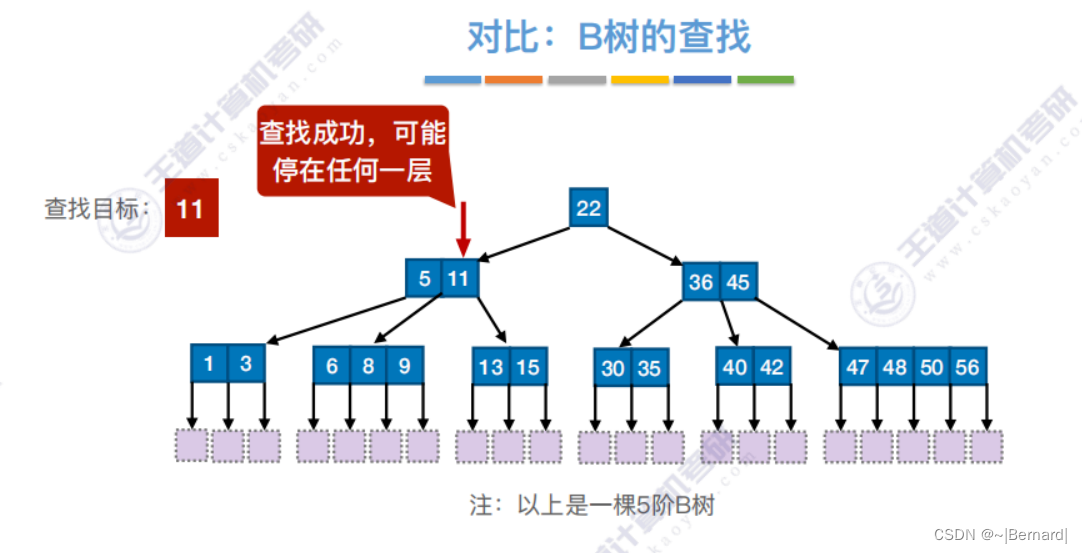
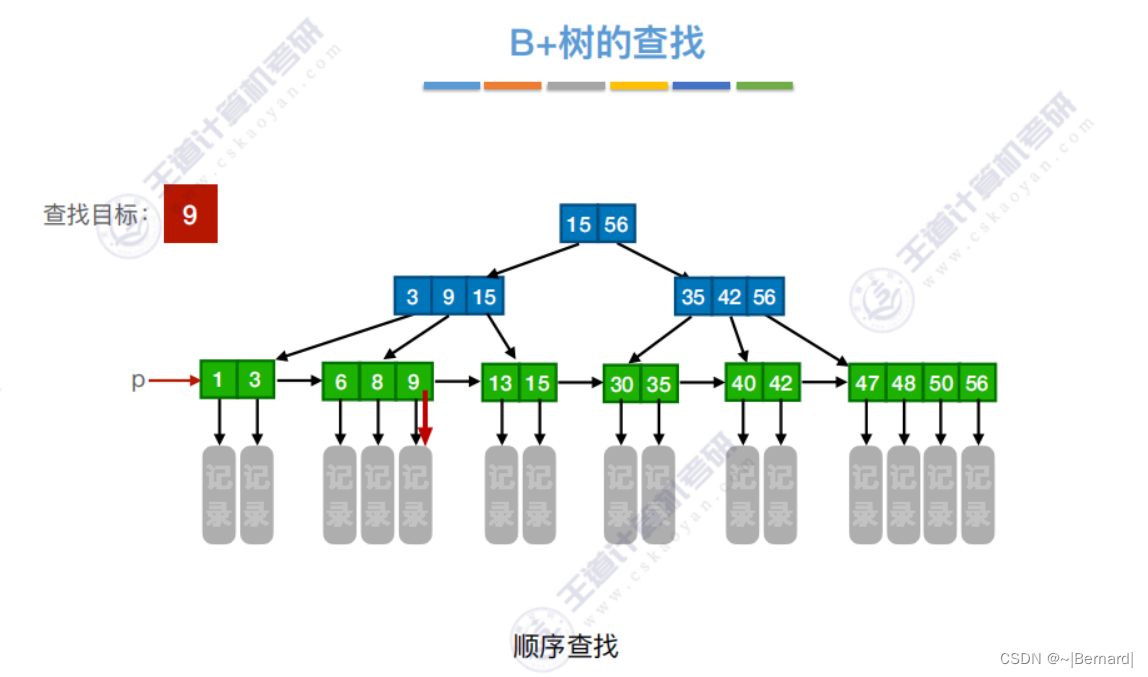
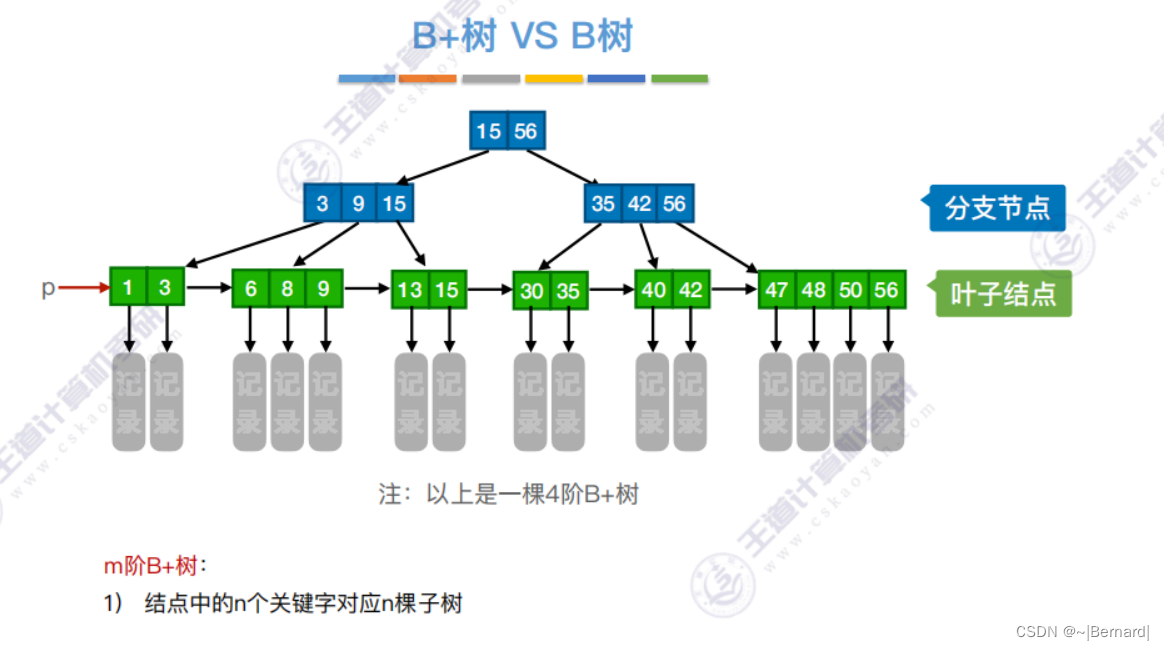
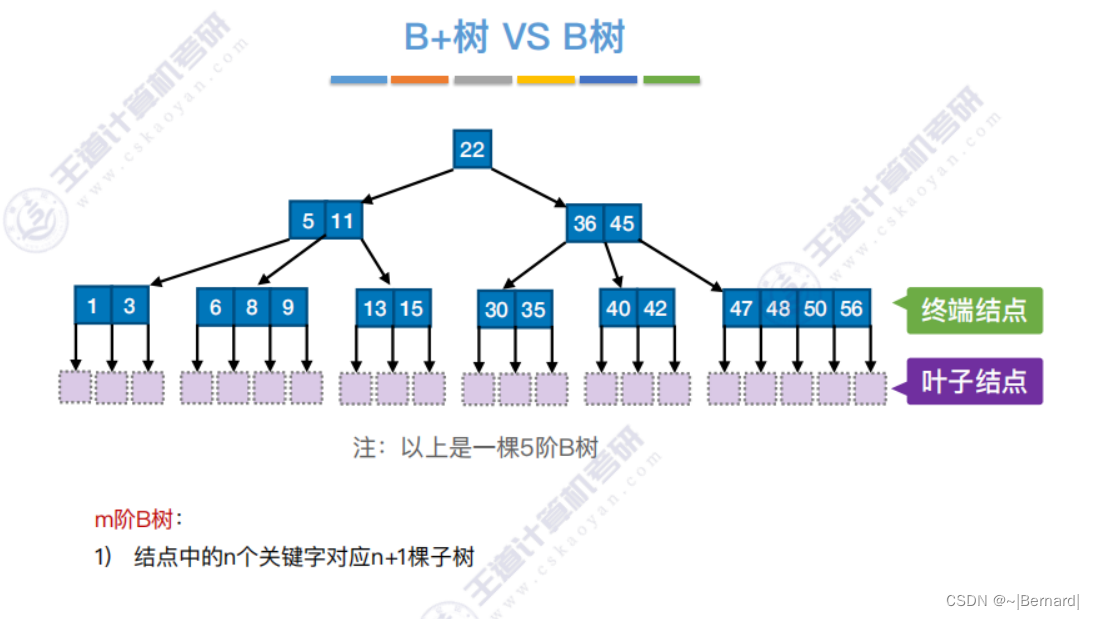
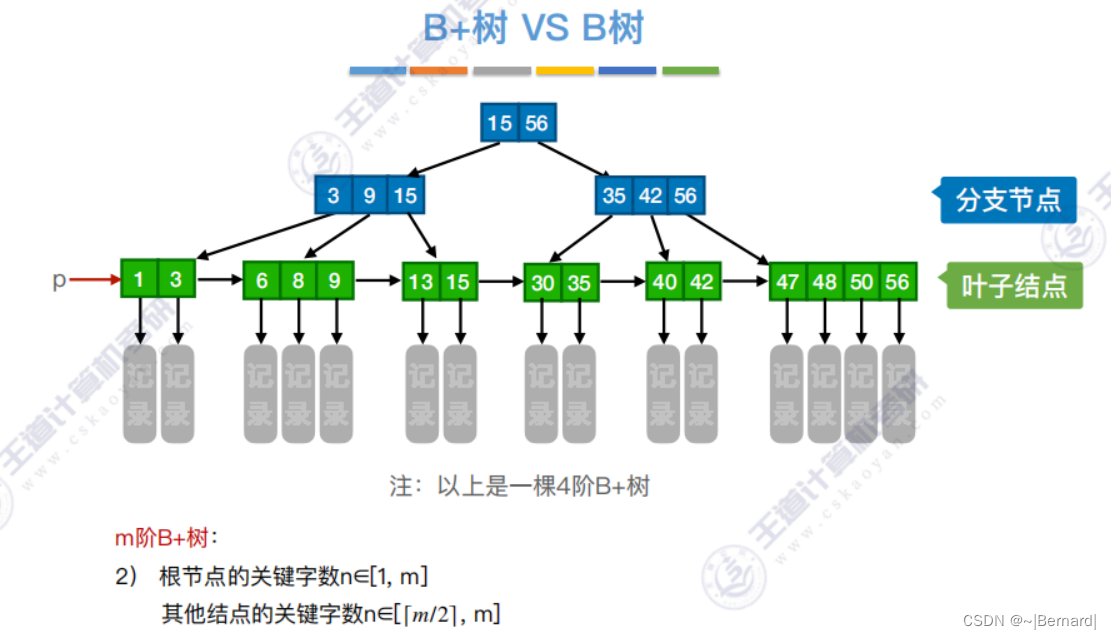
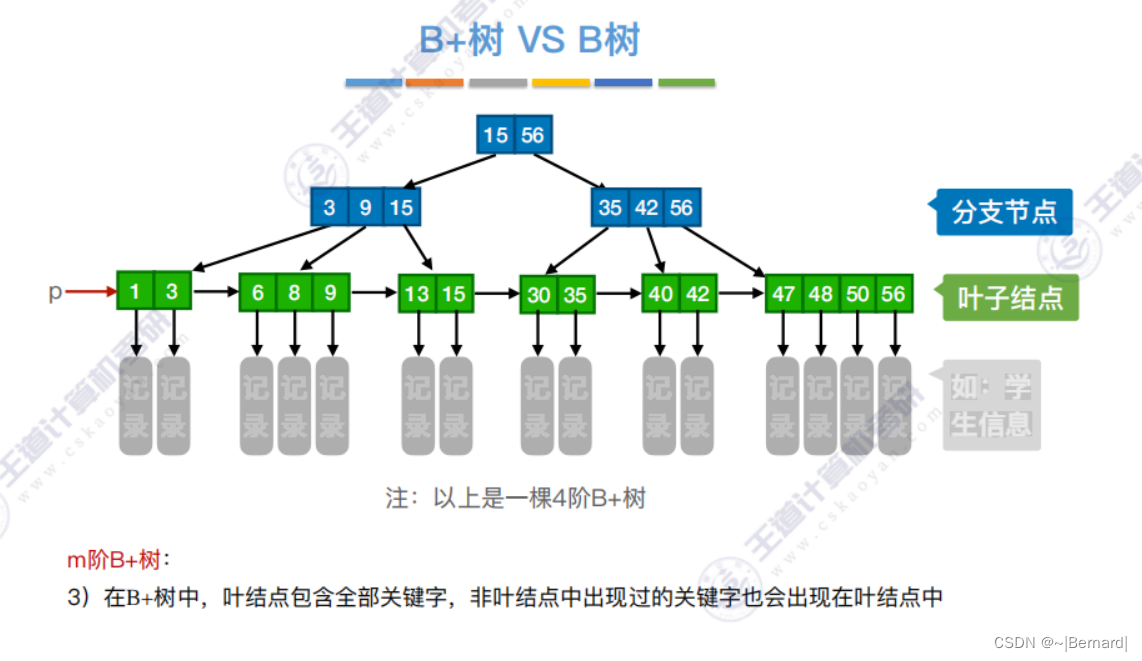
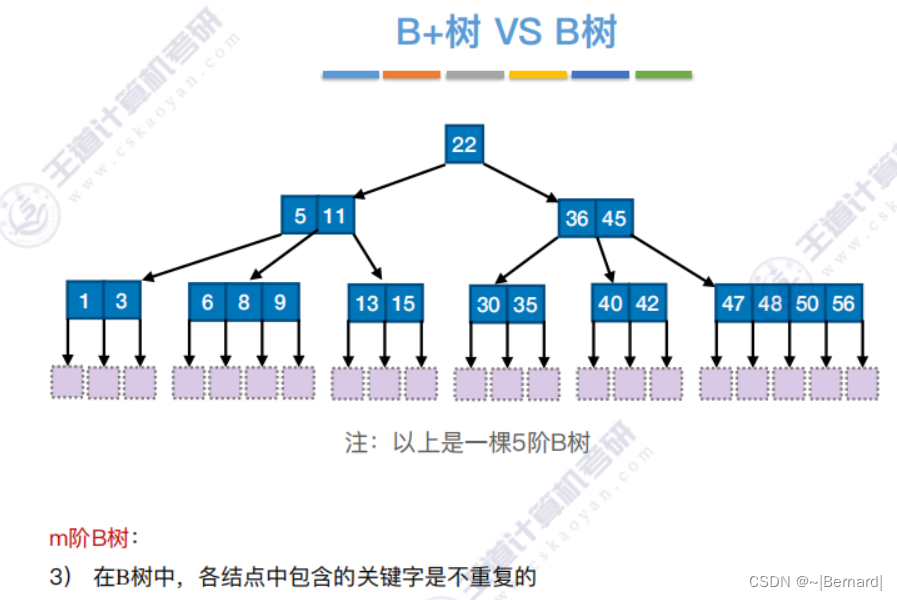
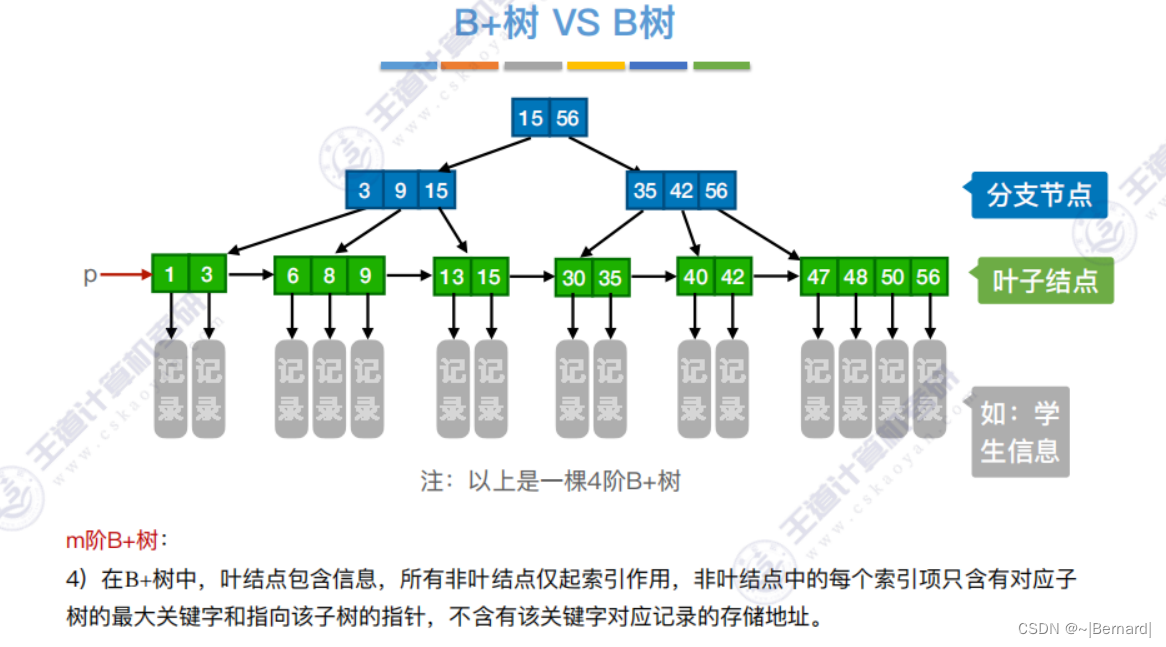
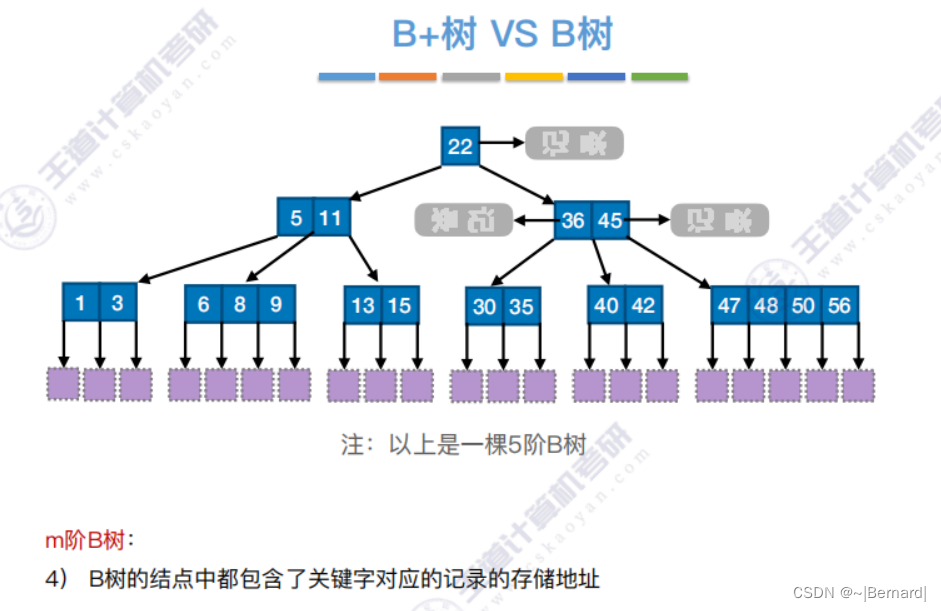
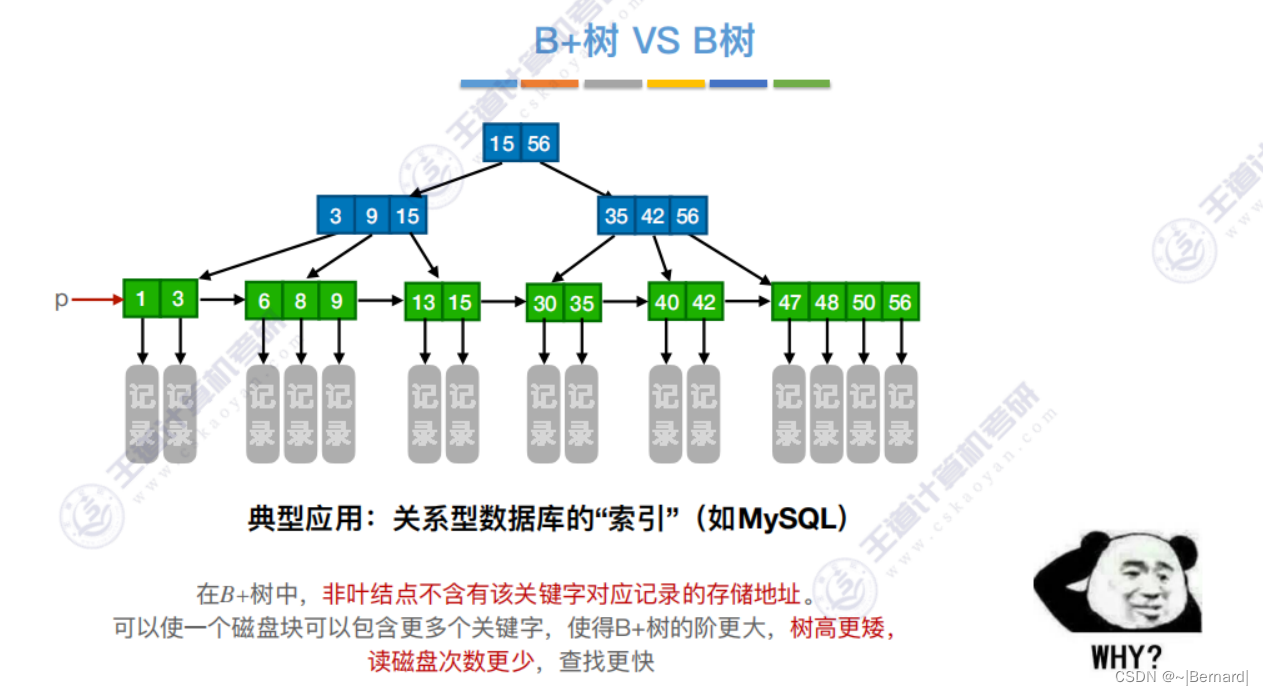
 注意：B+树的阶更大意思就是：分支数更多

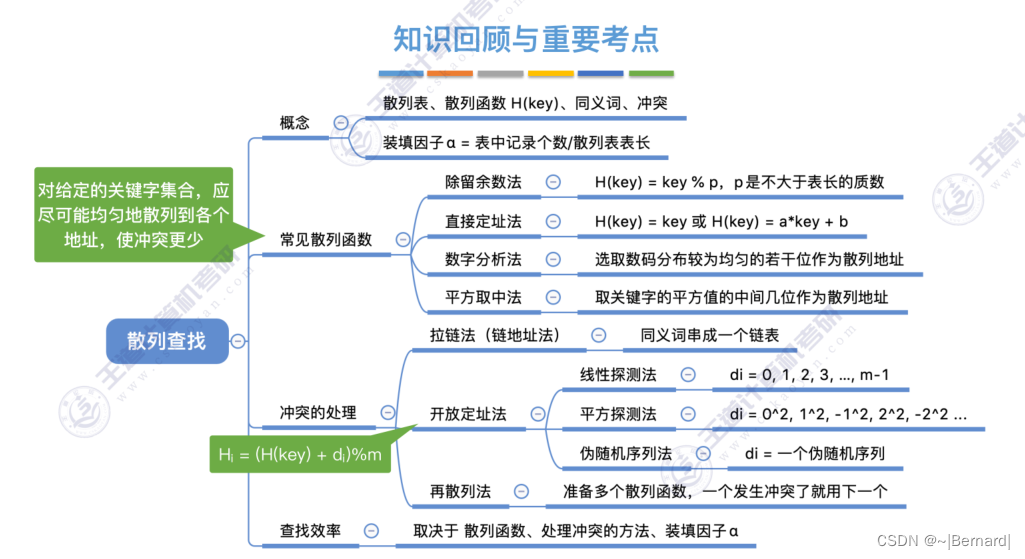
 7.5. 散列查找(详见课件)

注意：哈希映射是对小于表长的最大质数取模，而线性探测法是对表长进行取模。

注意：开放定址法删除元素的时候是进行标记(逻辑上的删除)而不是直接清空