VS——路径说明

news2024/10/7 14:28:24

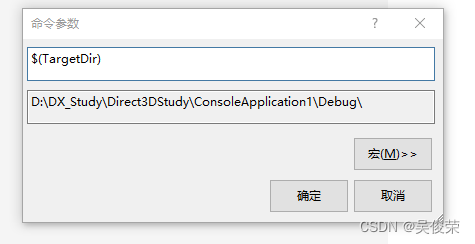
  1. $(TargetDir)输出目标的路径
    输出目标的路径

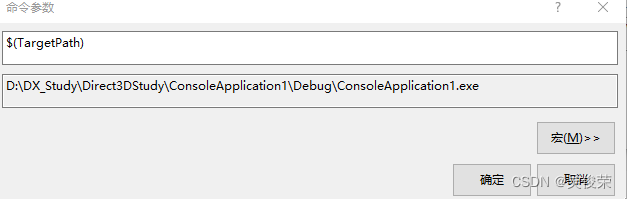
  2. $(TargetPath) 输出文件.exe的路径
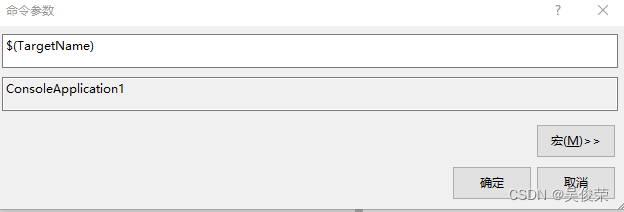
    在这里插入图片描述

  3. $(TargetName) 项目名字
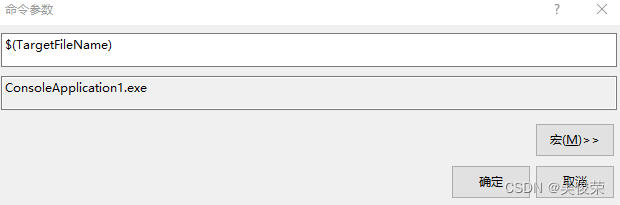
    在这里插入图片描述

  4. $(TargetFileName) 输出的.exe的名字
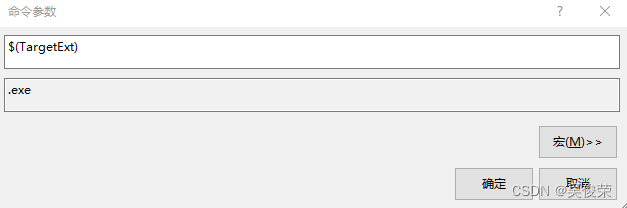
    在这里插入图片描述

  5. $(TargetExt) 文件的扩展名
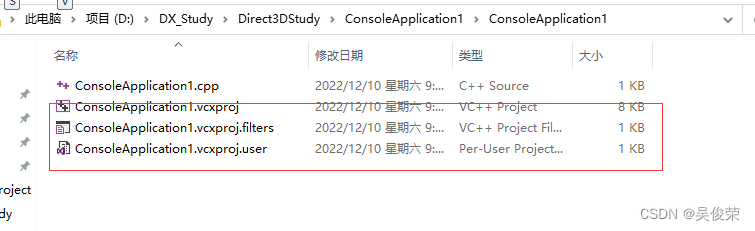
    在这里插入图片描述

  6. $(ProjectDir)工程目录
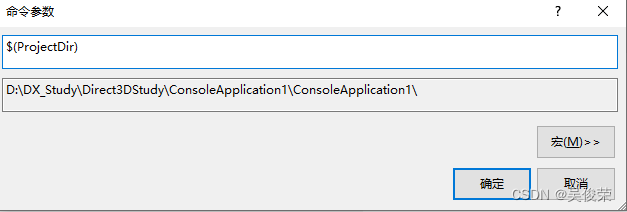
    在这里插入图片描述
    目录根据下面的文件来的
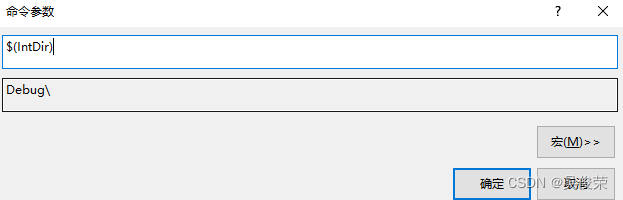
    在这里插入图片描述

  7. $(IntDir)获取中间文件
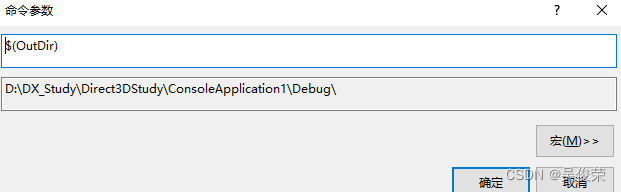
    在这里插入图片描述

  8. $(OutDir)文件输出路径
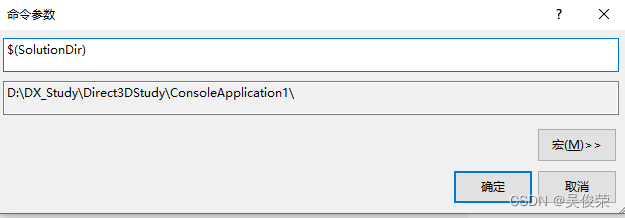
    在这里插入图片描述

  9. $(SolutionDir)解决方案的目录
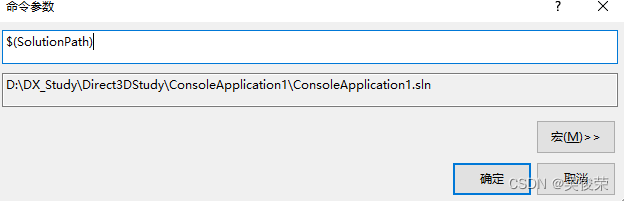
    在这里插入图片描述

  10. $(SolutionPath)解决方案的路径
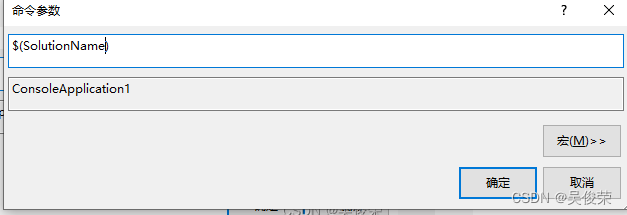
    在这里插入图片描述

  11. $(SolutionName)解决方案的名字
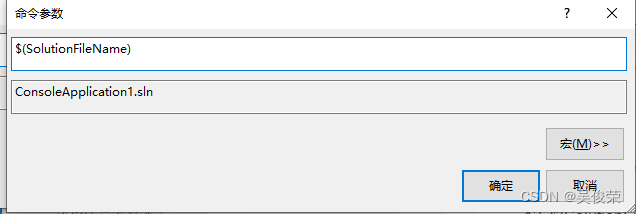
    在这里插入图片描述

  12. $(SolutionFileName)解决方案文件名字
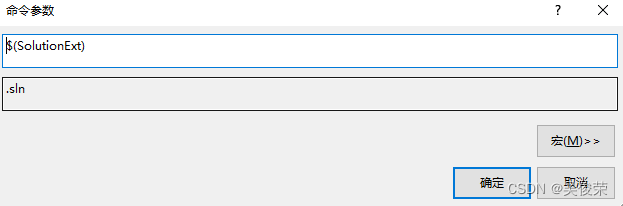
    在这里插入图片描述

  13. $(SolutionExt) 解决方案文件的扩展名
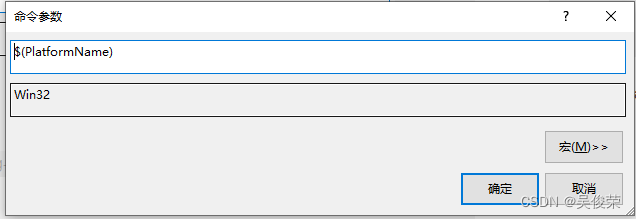
    在这里插入图片描述

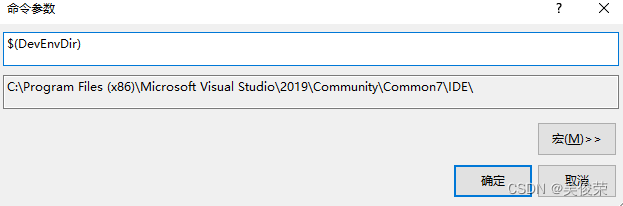
  14. $(PlatformName)平台名字在这里插入图片描述

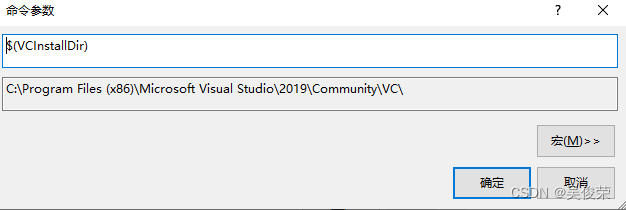
  15. $(DevEnvDir) IDE路径在这里插入图片描述
    16 . $(VCInstallDir)VC安装路径
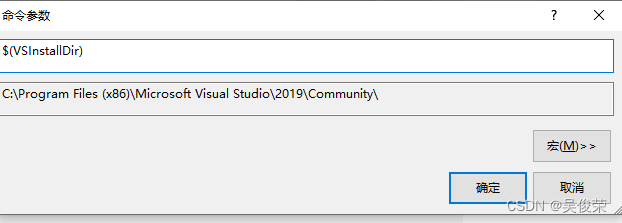
    在这里插入图片描述

  16. $(VSInstallDir)VS安装路径在这里插入图片描述

18.$(FrameworkDir)Framework路径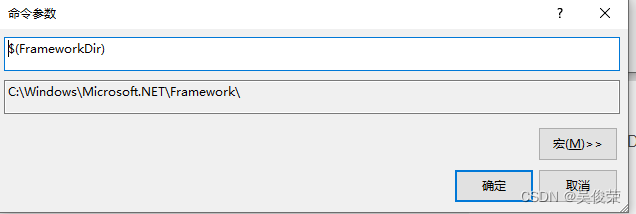在这里插入图片描述

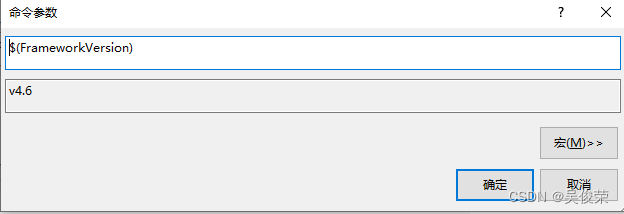
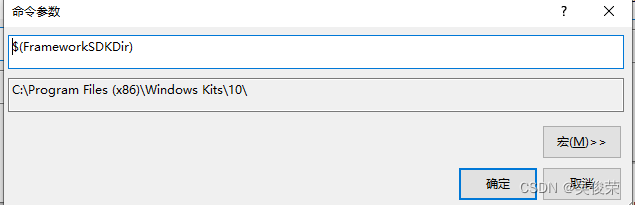
19.$(FrameworkVersion)Framework版本在这里插入图片描述

  1. $(FrameworkSDKDir)FrameworkSDK路径在这里插入图片描述

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/77171.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

神马操作Kafka 竟宣布弃用 Java 8

神马操作Kafka 竟宣布弃用 Java 8

Kafka 3.0.0 发布了： ​ 编辑切换为居中 添加图片注释，不超过 140 字（可选） 主要更新如下： The deprecation of support for Java 8 and Scala 2.12 Kafka Raft support for snapshots of the metadata topic and ot…
阅读更多...
ADI Blackfin DSP处理器-BF533的开发详解15：RS232串口的实现（含源代码）

ADI Blackfin DSP处理器-BF533的开发详解15：RS232串口的实现（含源代码）

硬件准备 ADSP-EDU-BF533：BF533开发板 AD-HP530ICE：ADI DSP仿真器 软件准备 Visual DSP软件 硬件链接 实现原理 ADSP-EDU-BF533 开发板上设计了一个 RS232 接口，该接口通过 ADSP-BF53x 上的 UART 接口，扩展 RS232协议的芯片实…
阅读更多...
Java学习之Object类——equals方法

Java学习之Object类——equals方法

Object 类是类层次结构的根类。每个类都使用 Object 作为超类。所有对象（包括数组）都实现这个类的方法，学习Object 类的六个方法——equals(Object obj)、finalize、toString、hashCode、getClass、clone 目录 和equals的对比 一、的作用 …
阅读更多...
ChatGPT惊人语录大赏

ChatGPT惊人语录大赏

文 | 智商掉了一地这几天ChatGPT实在太火了，笔者的朋友圈已经被ChatGPT的各种金句刷屏了，实在忍不住整理下来，分享给大家。ChatGPT惊人语录1：建议娶奶奶为妻注：贾母是贾宝玉的奶奶ChatGPT惊人语录2：角色扮演…
阅读更多...
【allegro 17.4软件操作保姆级教程十】文件输出

【allegro 17.4软件操作保姆级教程十】文件输出

目录 1.1添加光绘层叠 1.1.1添加线路层 1.1.2添加表底阻焊层 1.1.3添加表底钢网层 1.1.4添加表底丝印层 1.1.5添加钻孔层 ​1.2输出文件 1.2.1输出光绘文件 1.2.2输出钻孔文件 1.2.3输出坐标文件 1.2.4输出文件打包 1.1添加光绘层叠 在输出文件之前需要先添加光绘层…
阅读更多...
PyTorch中学习率调度器可视化介绍

PyTorch中学习率调度器可视化介绍

神经网络有许多影响模型性能的超参数。一个最基本的超参数是学习率(LR)，它决定了在训练步骤之间模型权重的变化程度。在最简单的情况下，LR值是0到1之间的固定值。 选择正确的LR值是具有挑战性。一方面较大的学习率有助于算法快速收敛，但它也…
阅读更多...
【车载开发系列】UDS诊断---输入输出控制（$0x2F）

【车载开发系列】UDS诊断---输入输出控制（$0x2F）

【车载开发系列】UDS诊断—输入输出控制（$0x2F） UDS诊断---输入输出控制（$0x2F）【车载开发系列】UDS诊断---输入输出控制（$0x2F）一.概念定义1）与0x31例程控制服务的关系2）与0x22读取…
阅读更多...
数据传送类指令（PUSH,POP,LEA)

数据传送类指令（PUSH,POP,LEA)

目录 数据传送类指令 堆栈的概念： 进栈指令 （PUSH） 出栈指令（POP） 练习 LEA取偏移地址（有效地址EA）指令（去括号） LEA和OFFSET区别： 用法注意 LEA和MO…
阅读更多...
微服务框架 SpringCloud微服务架构 微服务保护 31 限流规则 31.6 热点参数限流

微服务框架 SpringCloud微服务架构 微服务保护 31 限流规则 31.6 热点参数限流

微服务框架 【SpringCloudRabbitMQDockerRedis搜索分布式，系统详解springcloud微服务技术栈课程|黑马程序员Java微服务】 微服务保护 文章目录微服务框架微服务保护31 限流规则31.6 热点参数限流31.6.1 热点参数限流31.6.2 案例31 限流规则 31.6 热点参数限流 3…
阅读更多...
【代码审计-.NET】基于.NET框架开发的基本特征

【代码审计-.NET】基于.NET框架开发的基本特征

目录 一、.NET基本架构 1、基本构成 2、可支持语言 3、封装 4、文件 5、指向解析 6、安全认证 二、工具 1、ILSpyi 2、dnSpy 3、Reflector （网上找的一张图谱） 本博客只面向讲安全相关内容 一、.NET基本架构 1、基本构成 可支持语言&#xf…
阅读更多...
web shell控制目标

web shell控制目标

文章目录一、封神台五1、为什么提权2、如何寻找exp3、使用exp提权一、封神台五 1、为什么提权 进入目标机器后权限可能不够导致无法执行高权限操作 右键地址进入终端 发现没有操作权限 提权原理：借助高权限的进程执行我们的指令 2、如何寻找exp 什么是exp&a…
阅读更多...
【MOSMA】基于粘菌算法求解多目标优化问题附matlab代码

【MOSMA】基于粘菌算法求解多目标优化问题附matlab代码

✅作者简介：热爱科研的Matlab仿真开发者，修心和技术同步精进，matlab项目合作可私信。 🍎个人主页：Matlab科研工作室 🍊个人信条：格物致知。 更多Matlab仿真内容点击👇 智能优化算法 …
阅读更多...
【Java版oj】day02倒置字符串

【Java版oj】day02倒置字符串

目录 一、原题再现 二、问题分析 三、完整代码 一、原题再现 倒置字符串_牛客题霸_牛客网 描述 将一句话的单词进行倒置，标点不倒置。比如 I like beijing. 经过函数后变为：beijing. like I 输入描述： 每个测试输入包含1个测试用例&#x…
阅读更多...
web前端期末大作业 html+css+javascript+jquery+bootstarp响应式鲜花售卖网站16页

web前端期末大作业 html+css+javascript+jquery+bootstarp响应式鲜花售卖网站16页

🎉精彩专栏推荐 💭文末获取联系 ✍️ 作者简介: 一个热爱把逻辑思维转变为代码的技术博主 💂 作者主页: 【主页——🚀获取更多优质源码】 🎓 web前端期末大作业： 【📚毕设项目精品实战案例 (10…
阅读更多...
最新最全面的Java面试题及答案（212道）

最新最全面的Java面试题及答案（212道）

文章目录一. Java 基础1. JDK 和 JRE 有什么区别？2. 和 equals 的区别是什么？3. 两个对象的 hashCode() 相同，则equals() 也一定为true，对吗？4. final 在 Java 中有什么作用？5. Java 中的 Math. round(-1.…
阅读更多...
【图像分割】基于Kmean聚类 分水岭、oust、粒子群算法优化脂肪肝图像分割附matlab代码

【图像分割】基于Kmean聚类 分水岭、oust、粒子群算法优化脂肪肝图像分割附matlab代码

✅作者简介：热爱科研的Matlab仿真开发者，修心和技术同步精进，matlab项目合作可私信。 🍎个人主页：Matlab科研工作室 🍊个人信条：格物致知。 更多Matlab仿真内容点击👇 智能优化算法 …
阅读更多...
OPT（奥普特）工控机新品上市，产品矩阵再扩大

OPT（奥普特）工控机新品上市，产品矩阵再扩大

近日，OPT（奥普特）发布工控机新品，进一步扩展产品矩阵，为制造业数字化转型提供更为全面的机器视觉产品和服务。 OPT（奥普特）上市的工控机共有两大系列，分别是3U桌面式和4U上架式的设…
阅读更多...
【金猿人物展】映盛中国CEO谭运猛博士：数字化逆向重构将会占据行业红利成为新宠...

【金猿人物展】映盛中国CEO谭运猛博士：数字化逆向重构将会占据行业红利成为新宠...

‍谭运猛本文由映盛中国创始人兼CEO谭运猛撰写并投递参与“数据猿年度金猿策划活动——2022大数据产业趋势人物榜单及奖项”评选。‍数据智能产业创新服务媒体——聚焦数智 改变商业2022年伴随着新冠疫情的反复和经济下行的持续影响，各行各业都面临着数字化转型的行…
阅读更多...
【每日小技巧】如果Tomcat的端口被占用，怎么处理该报错

【每日小技巧】如果Tomcat的端口被占用，怎么处理该报错

苦恼的问题：当我们在用Tomcat时，发现我们要用的端口被其他程序占用了，如图： 解决办法： ①winR，输入cmd，打开命令行 输入命令netstat -ano，列出所有的端口号使用情况 ②查看PID&#…
阅读更多...
矩阵理论复习（四）

矩阵理论复习（四）

2003年试题 向量二范数也具有酉不变性 Schur定理的应用 向量范数的判定 向量范数的比较 酉矩阵的M-P广义逆就为该矩阵的转置 列满秩矩阵的左逆 一个矩阵乘以其逆矩阵等于单位矩阵，单位矩阵的算子范数均为1，算子范数的相容性 正规矩阵的性质 …
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023