矩阵理论复习（四）

news2024/10/7 16:16:18

2003年试题

向量二范数也具有酉不变性
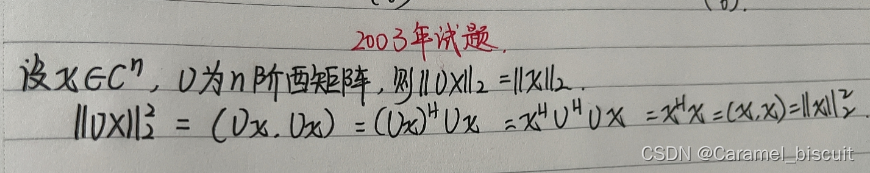
在这里插入图片描述
Schur定理的应用

向量范数的判定
在这里插入图片描述
向量范数的比较

酉矩阵的M-P广义逆就为该矩阵的转置

列满秩矩阵的左逆

一个矩阵乘以其逆矩阵等于单位矩阵，单位矩阵的算子范数均为1，算子范数的相容性
在这里插入图片描述

正规矩阵的性质
在这里插入图片描述

矩阵的特征值小于等于其任意相容的矩阵范数
在这里插入图片描述
范数的性质

严格对角占优矩阵必可逆
在这里插入图片描述
盖尔圆盘定理

正规矩阵可以酉相似对角化
在这里插入图片描述

A的最大秩分解
在这里插入图片描述

求矩阵的谱分解，求矩阵的高次幂
在这里插入图片描述

A^HA与AA^H非零特征值相等
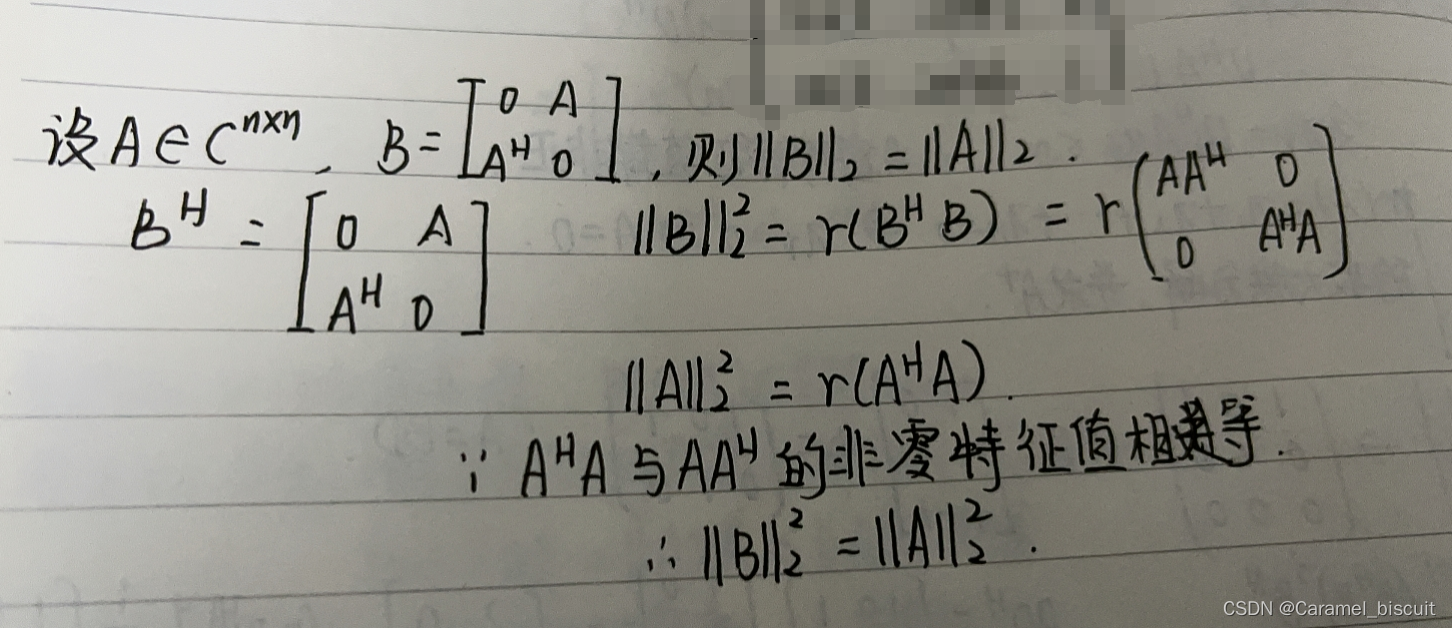
在这里插入图片描述

自相容矩阵范数的性质
在这里插入图片描述

Hermite矩阵的性质
在这里插入图片描述
n阶实阵的圆盘两两互不相交

严格对角占优矩阵的性质
在这里插入图片描述
Schur不等式

特征值的实部和虚部界限
在这里插入图片描述

特征值与奇异值之间的关系
在这里插入图片描述

求谱半径
在这里插入图片描述

证明为矩阵范数
在这里插入图片描述

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/77141.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

嵌入式：ARM的工作模式与寄存器组织

文章目录特权模式处理器启动时的模式转换图ARM的寄存器组织ARM寄存器组成概述ARM状态下的寄存器组织Thumb状态下的寄存器组织CPSR（当前程序状态寄存器）的低5位用于定义当前操作模式 , 如图示特权模式除用户模式外的其他6种模式称为特权模式。特权模式…

nodejs基于vue技术的小饰品购物商城网站

开发语言：nodejs 框架：Express 数据库：mysql 数据库工具：Navicat11 开发软件：VS code/HBuilder X 浏览器：谷歌浏览器目录 1 绪论 1 1.1课题背景 1 1.2课题研究现状 1 1.3初步设计方法与实施方案 2 1.4本…

【C++常用容器】STL基础语法学习queue容器

目录 ●queue的基本概念 ●queue常用接口 ●构造函数 ●赋值操作 ●数据存取 ●大小操作 ●queue的基本概念简要介绍：queue是一种先进先出的的数据结构，它有两个出口。队列容器允许从一端新增元素，从另一端移除元素。队列中只有队…

如何批量查询谷歌PR权重是多少？谷歌PR权重怎么批量查询

权重是就是网站在搜索引擎心目中的位置，如果一个网站在搜索引擎心目中的位置高的话，当然容易获得较好的排名，今天不是来跟大家聊如何提升网站权重的，而是教大家如何去看一个网站的权重，做网站的朋友都要知道要做关键词…

RadSystems Studio构建CRUD操作程序

RadSystems Studio构建CRUD操作程序 RadSystems Studio是一个快节奏的开发环境，不需要专门的编程。该软件提供了数字解决方案和组件，以尽快在API和UI中构建程序，只需少量代码，甚至无需编写。该软件减少了编写时间并改进了开发过程…

win10 安装配置nvm

第一步:下载安装包链接：https://pan.baidu.com/s/1B_gc9DnM8s3utcd_DB1H4Q?pwdxm03 提取码：xm03 第二步:安装nvm 第三步:配置nvm setting文件加上淘宝镜像 node_mirror: https://npm.taobao.org/mirrors/node/ npm_mirror: https://npm.taobao.or…

【python】os.system() os.popen() 在 python 执行 cmd 指令

先说总结 os.system：获取程序执行命令的返回值。 os.popen： 获取程序执行命令的输出结果。 commands：获取返回值和命令的输出结果。1 os.system() 这个方法是直接调用标准C的system() 函数，仅仅在一个子终端运行系统命令&#x…

代码实现 #include <iostream> #include <queue> using namespace std; template <typename T> class My_queues { private: //队列数据存储空间 T *data; //头下标 int head; //尾下标 int tail; int max_len; public: //无参构造函数 My_queues():data(NUL…

信息搜集方法总结

文章目录前言一、域名和IP信息搜集（一）判断是否使用CDN（二）存在CND时查找真实IP（三）WHOIS信息查询（四）备案信息查询（五）给定IP反查其他信息（六&am…

实现微信通知提醒的方法总结

一、使用企业微信群机器人接口效果：微信群消息通知优点：后台运行不受干扰性能稳定、群内多人同时接收通知、无需登录微信、支持微信图文消息缺点：只适用于企业微信群、有发送频率限制使用方法： 1、拉一个企业微信群，在…

TACL 2022 | GAL：合成文本在自然语言处理任务中的应用

©PaperWeekly 原创作者 | 何玄黎单位 | 伦敦大学学院（UCL）研究方向 | 自然语言处理论文标题：Generate, Annotate, and Learn: NLP with Synthetic Text收录会议：TACL 2022论文链接：https://arxiv.org/abs/2106.…

无需注册试用ChatGPT

无需注册试用ChatGPT OpenAI账号有诸多限制，包括地区限制，手机号注册等，参考ChatGPT注册试用全攻略。不开全局代理，还会出现Not available OpenAIs services are not available in your country. 所以有没有什么途径，…

ADI Blackfin DSP处理器-BF533的开发详解17：IIS+AUDIO音频codec的应用（含源代码）

硬件准备 ADSP-EDU-BF533：BF533开发板 AD-HP530ICE：ADI DSP仿真器软件准备 Visual DSP软件硬件链接很早期做的设计，用的是TI的一颗音频codec，如果要放到今天，我肯定是用ADI的SigmaDSP了，ADI所有的Si…

【计算机图形学入门】笔记5：光栅化（三角形的离散化）

目录05光栅化（三角形的离散化）1.Canonical Cube to Screen 从标准立方体到屏幕1.屏幕是什么？What is a screen?2.光栅化是什么？Raster screen in German3.像素Pixel (FYI, short for “picture element”)4.使用以下矩阵公式将中…