A - Move RightA - Move Right

题目大意

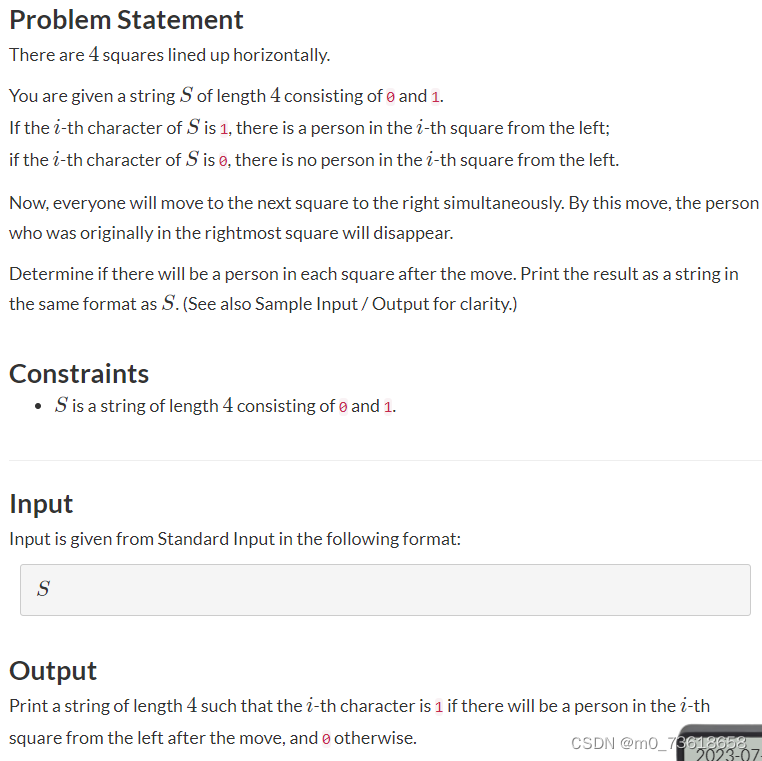
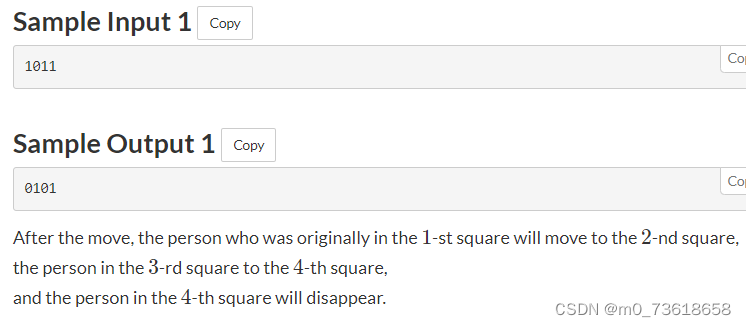
要求判断在一行4个方块上的人进行向右移动后，是否每个方块上都有人。初始状态下，给定一个由0和1组成的长度为4的字符串S，其中1表示对应方块上有人，0表示没有人。每个人同时向右移动一格，最右边的方块上的人将消失。

思路分析

直接构建移动后的状态字符串T

时间复杂度

O(1)

AC代码

#include <bits/stdc++.h>
using namespace std;

int main() {
  string S;
  cin >> S;
  
  string T = "0" + S.substr(0, 3);
  cout << T << endl;
}

B - Unique NicknamesB - Unique Nicknames

题目大意

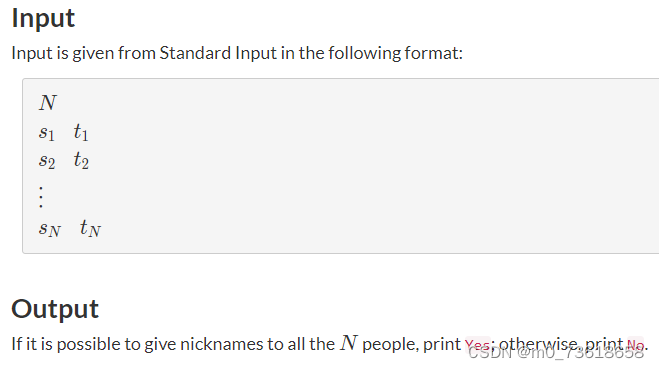
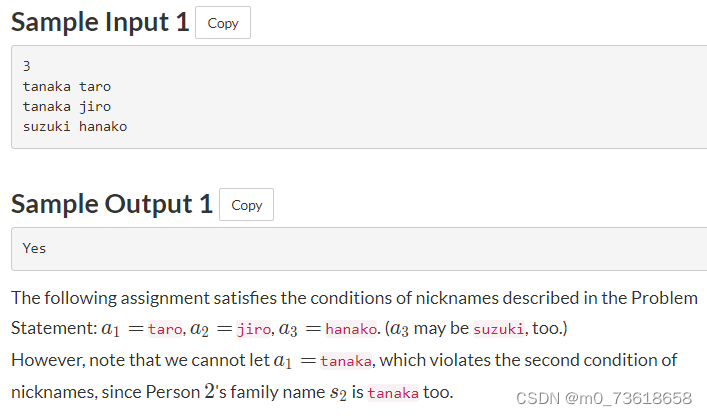
给定N个人，每个人有姓氏和名字。需要判断是否可能给所有人起一个符合条件的昵称，其中昵称必须与该人的姓氏或名字相同，并且不能与其他任何人的姓氏或名字相同。

思路分析

可以使用两层循环来解决这个问题。外层循环遍历每个人，内层循环尝试给当前人选择一个昵称（即姓氏或名字），并确保给每个人起昵称时都不会与其他人产生冲突。如果找到了一个满足条件的昵称，则说明可以给该人起昵称；否则，说明无法给该人起昵称。

时间复杂度

O(N²)

AC代码

#include <iostream>
#include <vector>
using namespace std;

int main() {
    int N;
    cin >> N;
    
    vector<string> s(N), t(N);
    for (int i = 0; i < N; i++) {
        cin >> s[i] >> t[i];
    }
    
    for (int i = 0; i < N; i++) {
        bool can_give_a_nickname = false;
        
        for (string S : {s[i], t[i]}) {
            bool s_ok = true;
            
            for (int j = 0; j < N; j++) {
                if (i != j) {
                    if (S == s[j] || S == t[j]) {
                        s_ok = false;
                    }
                }
            }
            
            if (s_ok == true) {
                can_give_a_nickname = true;
            }
        }
        
        if (can_give_a_nickname == false) {
            cout << "No" << endl;
            return 0;
        }
    }
    
    cout << "Yes" << endl;
    return 0;
}

C - 1 2 1 3 1 2 1

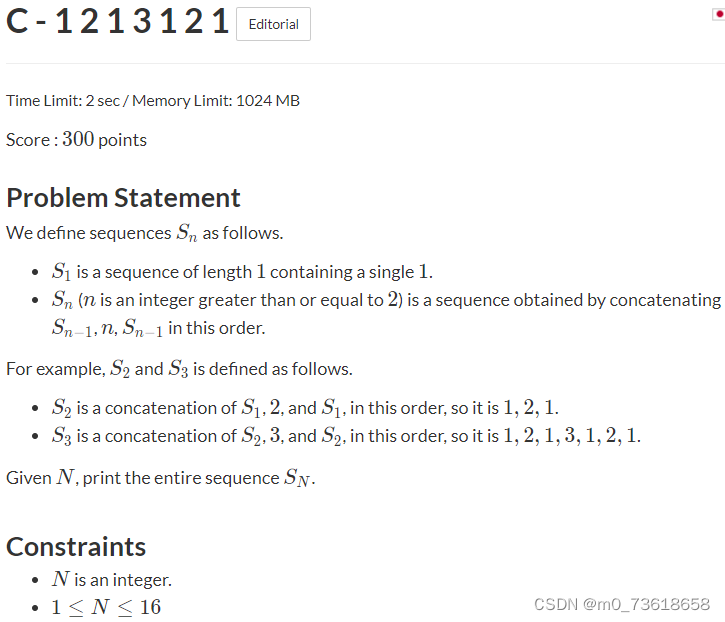
题目大意

定义序列 Sn 如下：
S1 是一个长度为1的序列，包含一个数字1。
对于 n >= 2，Sn 是通过将 S_n-1、n 和 S_n-1}按照顺序连接而得到的序列。
例如，S2 是将 S₁、2 和 S₁ 按照顺序连接而得到的，所以它是: 1, 2, 1。
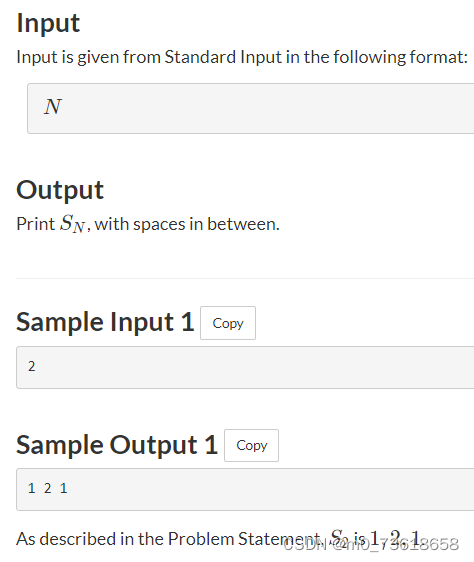
给定一个整数 N，输出完整的序列 SN。

思路分析

使用递归的方式来构造序列 SN。当 N=1 时，直接输出 “1”。对于 N>1 的情况，可以先构造 S_N-1，然后在其前后添加 N，并再次添加 S_N-1，即可得到 S_N。

时间复杂度

O(N)
在构造序列的过程中，需要进行 N-1 次递归调用。每次递归调用的时间复杂度为 O(1)

AC代码

#include <bits/stdc++.h>
using namespace std;
int main() {
    int n;
    cin >> n;
    string s = "1";
    for (int i = 2; i <= n; i++) {
        string t = s;
        s += " ";
        s += to_string(i);
        s += " ";
        s += t;
    }
   cout << fixed << setprecision(10);
  cout << s << endl;
}