数据结构-树的基本概念和堆

news2024/11/28 10:53:40

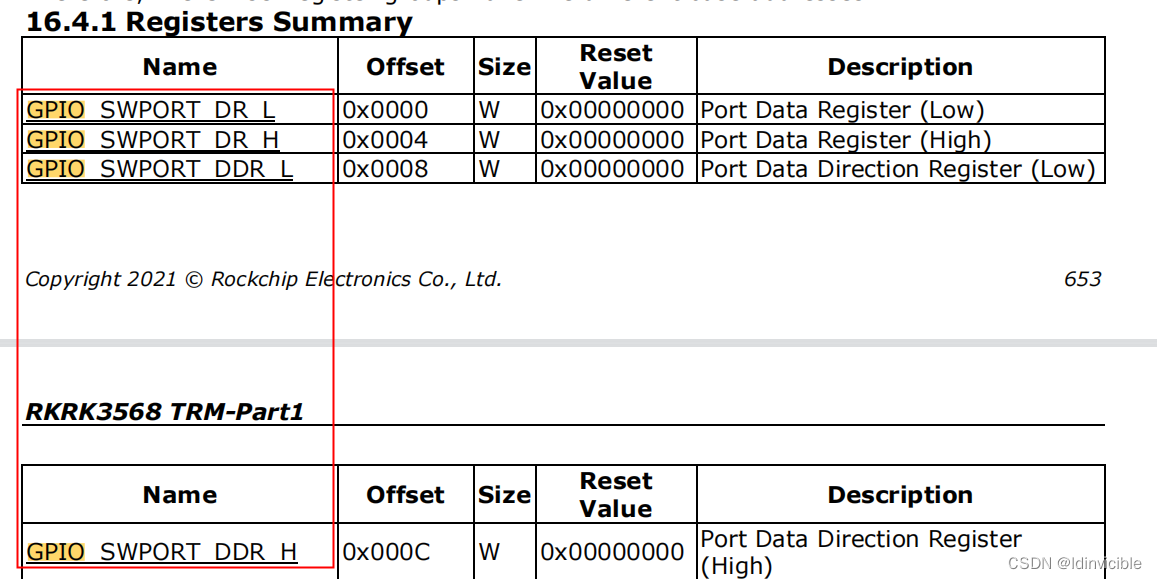
树的基本概念和堆

    • 树的基本概念
    • 堆的建立
    • 堆的信息
    • 堆的初始化
    • 堆的push（数据插入后，仍要遵守堆的规则）
    • 堆的pop
    • 根的元素值
    • 堆的大小
    • 堆的销毁
    • 演示一个过程，打印出该堆的前k个元素
    • 全部代码
      • Heap.h
      • Heap.c
      • Test.c
    • 堆的应用（排序）

树的基本概念

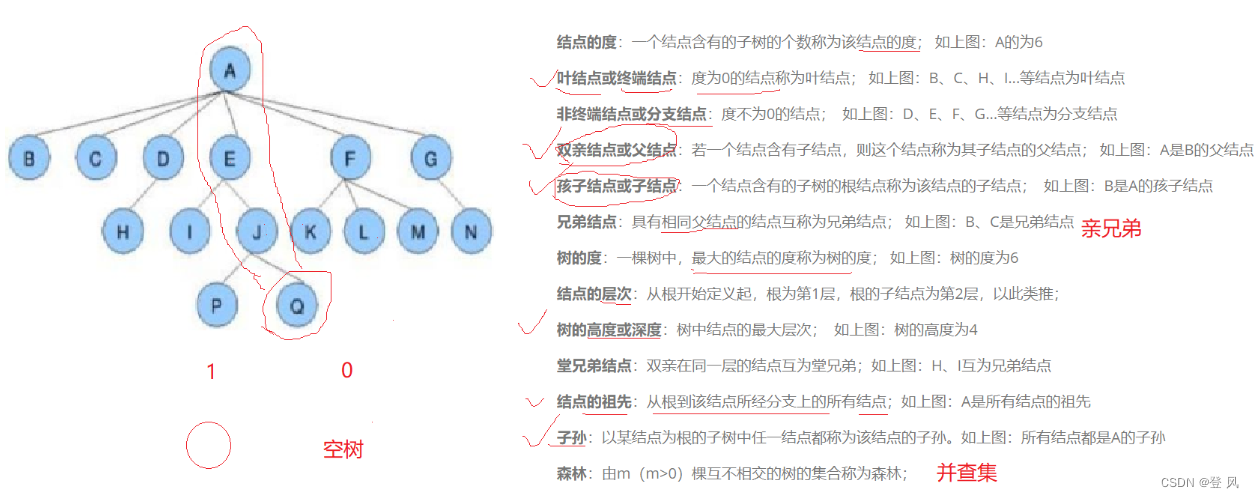
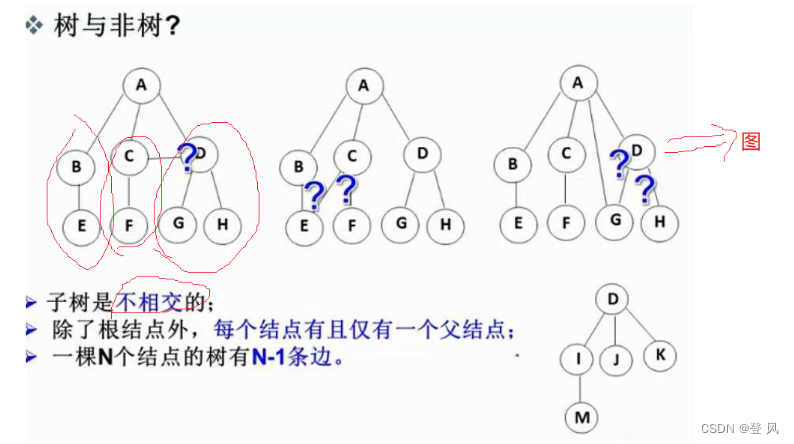
在这里插入图片描述
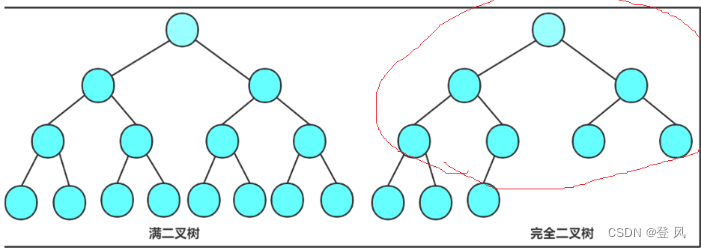
在这里插入图片描述
在这里插入图片描述
2.完全二叉树：在这里插入图片描述，最后一层要求至少要有一个结点
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述节点个数为N的完全二叉树的高度h为log以2为底N的对数。
在这里插入图片描述
在一颗度为3的树中，设度为i的节点个数为ni, 树总共有n个节点,则n=n0+n1+n2+n3. 有n个节点的树的总边数为n-1条.根据度的定义,总边数与度之间的关系为：n-1=0n0+1n1+2n2+3n3.

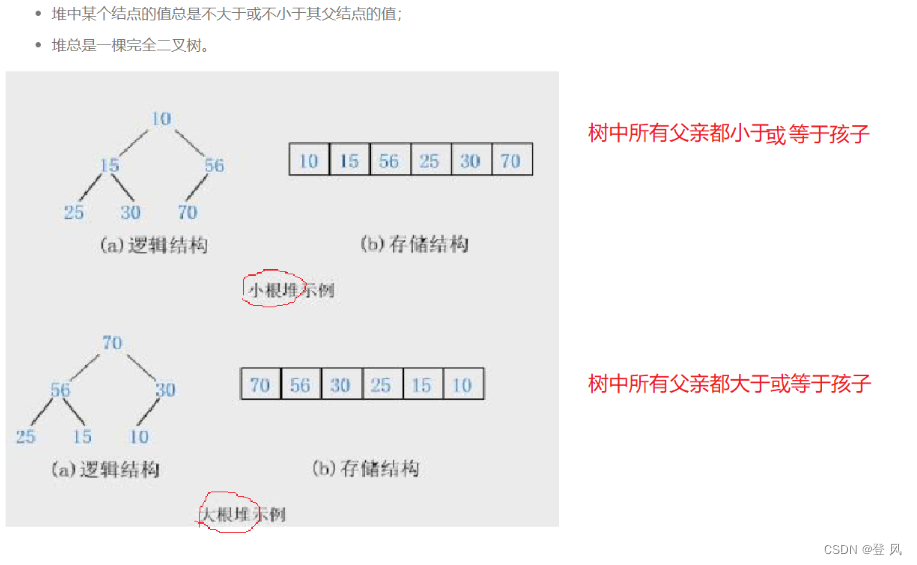
堆的基本概念
在这里插入图片描述

堆的建立

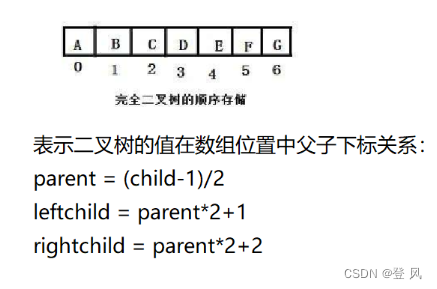
选用数组来表示堆的物理结构（存储结构）

堆的信息

用一个结构体来表示堆的信息：堆的空间，堆的大小，堆的容量

typedef struct Heap
{
	HPDataType* a;
	int size;
	int capacity;
}HP;

堆的初始化

断言，该结构体存在，其指针一定存在。为数组开辟空间，size和capacity初始化

void HPInit(HP* php)
{
	assert(php);

	php->a=(HPDataType*)malloc(sizeof(HPDataType) * 4);
	if (php->a==NULL)
	{
		perror("malloc fail");
		return;
	}

	php->size = 0;
	php->capacity = 4;
}

堆的push（数据插入后，仍要遵守堆的规则）

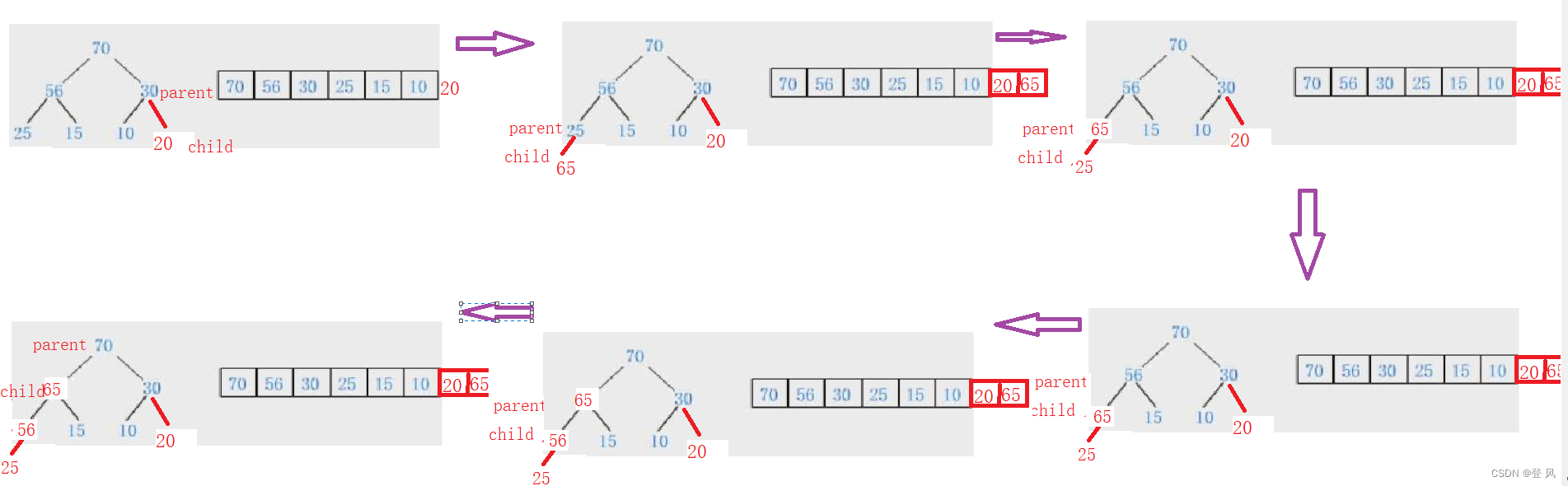
先检查是否需要扩容；直接插到堆的尾部，再做向上调整；
怎么向上调整？和它的parent节点比较，如果比parent小，则不做任何动作，结束； 如果比parent大，则交换child和parent节点的值，再进行和parent节点比较的操作，直至child节点的下标小于等于0（则，parent节点必然不会再有）

在这里插入图片描述

void swap(HPDataType* p1, HPDataType* p2)
{
	HPDataType temp;
	temp = *p1;
	*p1 = *p2;
	*p2 = temp;
}
void AdjustUp(HPDataType* a, int child)
{
	//先找到parent和child
	int parent = (child - 1) / 2;
	while (child>0)
	{
		if (a[child]>a[parent])
		{
			//交换值，递进到下一个parent和child
			swap(&a[child], &a[parent]);
			child = parent;
			parent = (child - 1) / 2;
		}
		else
		{
			//符合堆的要求，跳出循环
			break;
		}
	}
}
void HeapPush(HP* php, HPDataType x)
{
	assert(php);

	if (php->size==php->capacity)
	{
		HPDataType* temp = (HPDataType*)realloc(php->a, sizeof(HPDataType) * php->capacity * 2);
		if (temp==NULL)
		{
			perror("realloc fail");
			return;
		}

		php->a = temp;
		php->capacity = php->capacity * 2;
	}
	//直接插入尾部
	php->a[php->size++] = x;
	//向上调整
	AdjustUp(php->a, php->size - 1);
}

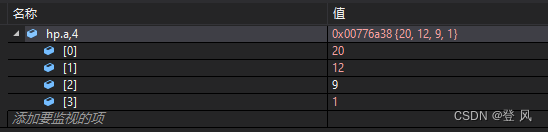
测试push的代码如下：

	HP hp;
	HPInit(&hp);

	HeapPush(&hp, 1);
	HeapPush(&hp, 12);
	HeapPush(&hp, 9);
	HeapPush(&hp, 20);

结果如下：
在这里插入图片描述

堆的pop

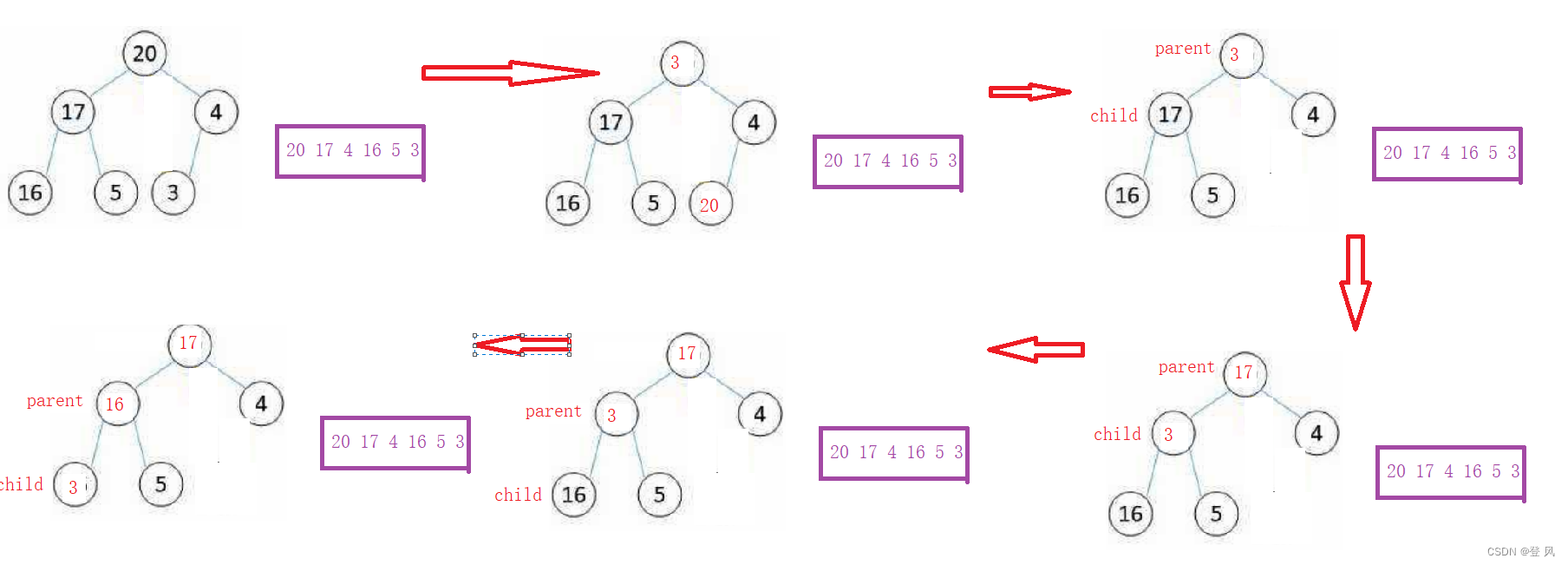
删除根，原因，现实世界，用于排序。
并不是直接删除，而是将根和尾节点进行交换，将尾节点删除，对根节点做向下调整。
怎么做向下调整？选择和较大的孩子节点作比较，如果比parent小，则不做任何动作，结束；如果比parent大，则交换child和parent节点的值，再进行和parent节点比较的操作，直至child节点的下标大于n（n为节点的个数size）

在这里插入图片描述

bool HeapEmpty(HP* php)
{
	assert(php);
	return php->size == 0;
}

void AdjustDown(HPDataType* a, int n, int parent)
{
	int child = parent * 2 + 1;

	while (child<n)
	{
		//找出最大的孩子
		if (child+1<n && a[child+1]>a[child])
		{
			child++;
		}

		if (a[parent] < a[child])
		{
			swap(&a[child], &a[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}

void HeapPop(HP* php)
{
	assert(php);
	assert(!HeapEmpty(php));

	swap(&php->a[0],&php->a[php->size-1]);
	//删尾
	php->size--;

	//向下调整
	AdjustDown(php->a, php->size, 0);
}

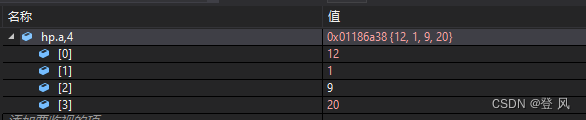
测试代码如下：

HP hp;
	HPInit(&hp);

	HeapPush(&hp, 1);
	HeapPush(&hp, 12);
	HeapPush(&hp, 9);
	HeapPush(&hp, 20);
	HeapPop(&hp);

结果如下：
在这里插入图片描述

根的元素值

直接返回a[0]

HPDataType HeapTop(HP* php)
{
	assert(php);
	return php->a[0];
}

堆的大小

直接返回size

HPDataType HeapSize(HP* php)
{
	assert(php);
	return php->size;
}

堆的销毁

void HPDestroy(HP* php)
{
	free(php->a);
	php->a = NULL;
	php->capacity = 0;
	php->size = 0;
}

演示一个过程，打印出该堆的前k个元素

代码如下：

	HP hp;
	HPInit(&hp);

	HeapPush(&hp, 1);
	HeapPush(&hp, 12);
	HeapPush(&hp, 9);
	HeapPush(&hp, 20);
	HeapPush(&hp, 27);
	HeapPush(&hp, 20);
	HeapPop(&hp);
	
	int k = 3;
	while (!HeapEmpty(&hp) && k--)
	{
		printf("%d ", HeapTop(&hp));
		HeapPop(&hp);
	}
	return 0;

结果如下：
在这里插入图片描述

全部代码

Heap.h

#pragma once
#include <stdio.h>
#include <assert.h>
#include <stdlib.h>
#include <stdbool.h>

typedef int HPDataType;
typedef struct Heap
{
	HPDataType* a;
	int size;
	int capacity;
}HP;


void HPInit(HP* php);
void HPDestroy(HP* php);

void HeapPush(HP* php, HPDataType x);
void HeapPop(HP* php);

HPDataType HeapTop(HP* php);
HPDataType HeapSize(HP* php);

bool HeapEmpty(HP* php);

//向上调整
void AdjustUp(HPDataType* a,int child);
//向下调整
void AdjustDown(HPDataType* a, int n, int parent);

Heap.c

#define _CRT_SECURE_NO_WARNINGS 1
#include "Heap.h"

void HPInit(HP* php)
{
	assert(php);

	php->a=(HPDataType*)malloc(sizeof(HPDataType) * 4);
	if (php->a==NULL)
	{
		perror("malloc fail");
		return;
	}

	php->size = 0;
	php->capacity = 4;
}

void swap(HPDataType* p1, HPDataType* p2)
{
	HPDataType temp;
	temp = *p1;
	*p1 = *p2;
	*p2 = temp;
}
void AdjustUp(HPDataType* a, int child)
{
	//先找到parent和child
	int parent = (child - 1) / 2;
	while (child>0)
	{
		if (a[child]>a[parent])
		{
			//交换值，递进到下一个parent和child
			swap(&a[child], &a[parent]);
			child = parent;
			parent = (child - 1) / 2;
		}
		else
		{
			//符合堆的要求，跳出循环
			break;
		}
	}
}
void HeapPush(HP* php, HPDataType x)
{
	assert(php);

	if (php->size==php->capacity)
	{
		HPDataType* temp = (HPDataType*)realloc(php->a, sizeof(HPDataType) * php->capacity * 2);
		if (temp==NULL)
		{
			perror("realloc fail");
			return;
		}

		php->a = temp;
		php->capacity = php->capacity * 2;
	}
	//直接插入尾部
	php->a[php->size++] = x;
	//向上调整
	AdjustUp(php->a, php->size - 1);
}

bool HeapEmpty(HP* php)
{
	assert(php);
	return php->size == 0;
}

void AdjustDown(HPDataType* a, int n, int parent)
{
	int child = parent * 2 + 1;

	while (child<n)
	{
		//找出最大的孩子
		if (child+1<n && a[child+1]>a[child])
		{
			child++;
		}

		if (a[parent] < a[child])
		{
			swap(&a[child], &a[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}

void HeapPop(HP* php)
{
	assert(php);
	assert(!HeapEmpty(php));

	swap(&php->a[0],&php->a[php->size-1]);
	//删尾
	php->size--;

	//向下调整
	AdjustDown(php->a, php->size, 0);
}

HPDataType HeapTop(HP* php)
{
	assert(php);
	return php->a[0];
}

HPDataType HeapSize(HP* php)
{
	assert(php);
	return php->size;
}

void HPDestroy(HP* php)
{
	free(php->a);
	php->a = NULL;
	php->capacity = 0;
	php->size = 0;
}

Test.c

#define _CRT_SECURE_NO_WARNINGS 1
#include "Heap.h"

int main()
{
	HP hp;
	HPInit(&hp);

	HeapPush(&hp, 1);
	HeapPush(&hp, 12);
	HeapPush(&hp, 9);
	HeapPush(&hp, 20);
	HeapPush(&hp, 27);
	HeapPush(&hp, 20);
	HeapPop(&hp);
	
	int k = 3;
	while (!HeapEmpty(&hp) && k--)
	{
		printf("%d ", HeapTop(&hp));
		HeapPop(&hp);
	}

	HPDestroy(&hp);
	return 0;
}

堆的应用（排序）

对数组进行排序，比如排升序.
一般情况下，我们会认为排升序，需要建小堆，但这种想法是不正确的，小堆的第一个元素没有问题，但是从第二个节点开始关系可能会混乱，还需要再进行建小堆，时间复杂度会增加。我们这里需要建大堆。
这里可以通过两种方式来建立大堆，向上调整建堆和向下调整建堆。

  • 向上调整建堆：从第二个元素开始，大的child和小的parent交换；
  • 向下调整建堆：从最后一个叶子的parent开始调整，大的child和小的parent交换，依次倒数

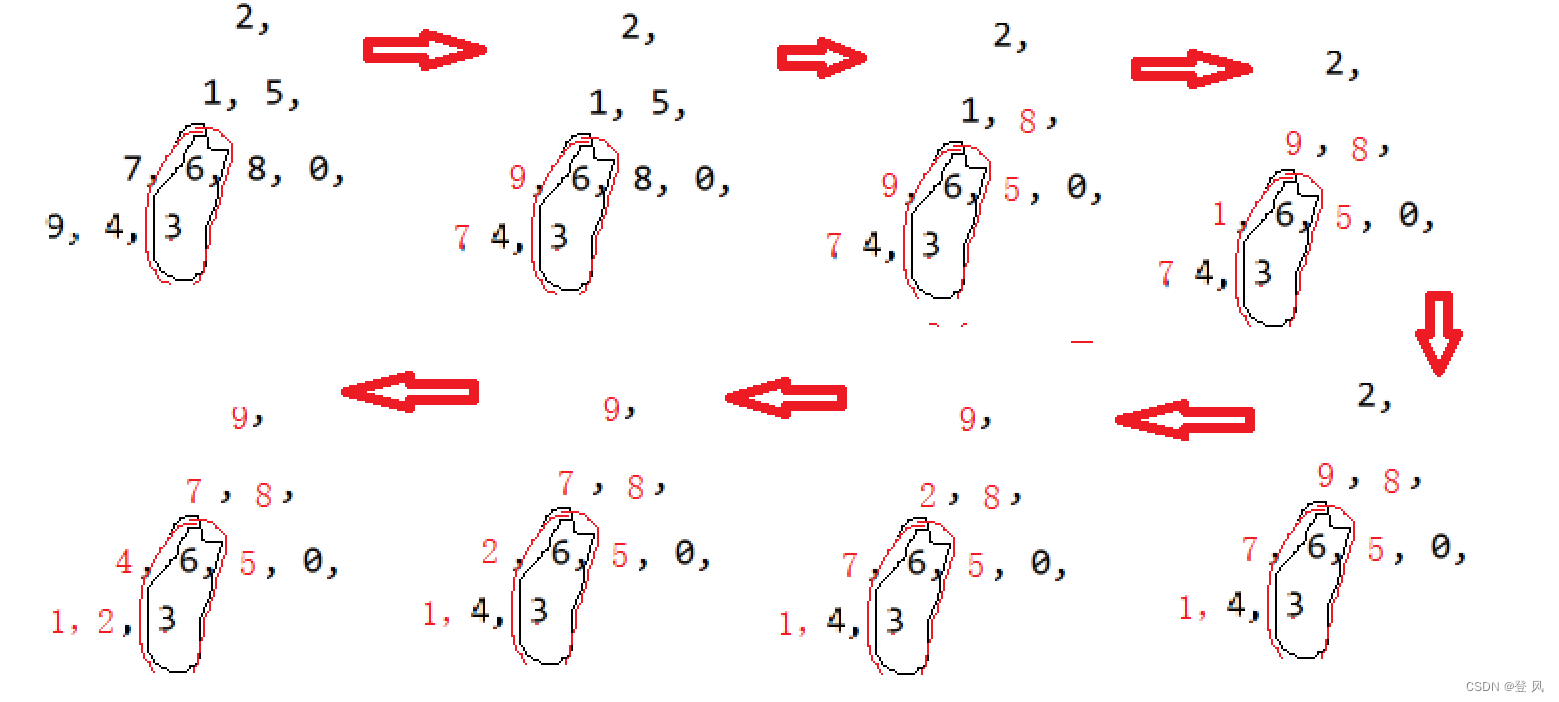
在这里插入图片描述
建完大堆后如何实现排序，首先大堆的根一定是最最大，让它和最后一个元素交换位置，则升序的最后一个数字便确定了下来；对此时的首元素向下调整，可以找到次大的元素；依次循环便可以排好序。

向上调整建堆的代码

void HeapSort(int* a, int n)
{
	//向上调整
	for (int i=1;i<n;i++)
	{
		AdjustUp(a, i);
	}

	int end = n - 1;
	while (end>0)
	{
		swap(&a[end], &a[0]);
		AdjustDown(a, end, 0);
		end--;
	}
}
int main()
{
	int a[10] = { 2, 1, 5, 7, 6, 8, 0, 9, 4, 3 };
	HeapSort(a,10);//排升序
	return 0;
}

结果如下：
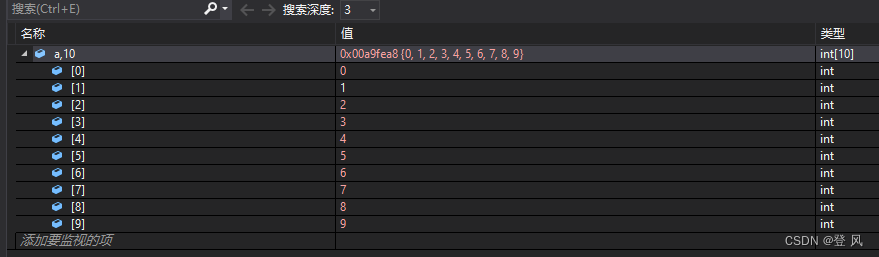
在这里插入图片描述
向下调整建堆的代码

void HeapSort(int* a, int n)
{
	//向上调整
	//for (int i=1;i<n;i++)
	//{
	//	AdjustUp(a, i);
	//}
	//向下调整
	for (int i = (n-1-1)/2; i>=0; i--)
	{
		AdjustDown(a,n,i);
	}

	int end = n - 1;
	while (end>0)
	{
		swap(&a[end], &a[0]);
		AdjustDown(a, end, 0);
		end--;
	}
}
int main()
{
	int a[10] = { 2, 1, 5, 7, 6, 8, 0, 9, 4, 3 };
	HeapSort(a,10);//排升序
	return 0;
}

结果如下：
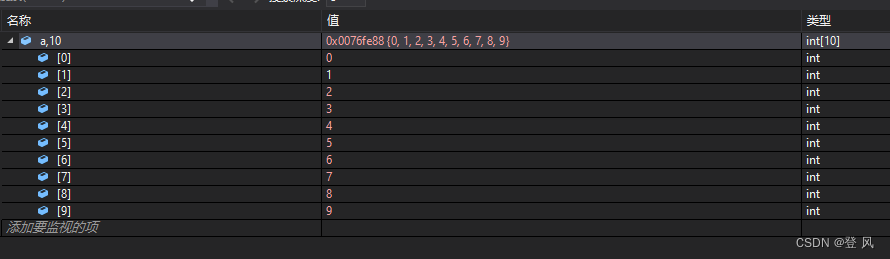
在这里插入图片描述

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/769397.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Python 下载安装总结

Python 下载安装总结

title: Python 下载安装总结 date: 2023-06-26 16:40:45 tags: Python categories:开发工具及环境 cover: https://cover.png feature: false 1. 下载 进入官网&#xff1a;Python.org&#xff0c;鼠标悬停在 Downloads&#xff0c;就会出现下载按钮 点击下载&#xff0c;即可…
阅读更多...
番外-sql server数据库表及视图未备份，误删恢复

番外-sql server数据库表及视图未备份，误删恢复

&#xff08;1&#xff09;关闭sql server服务&#xff0c;防止数据发生更大变化&#xff1b;备份数据库的ldf文件和mdf文件&#xff08;非常重要&#xff09; &#xff08;2&#xff09;安装工具ApexSQLLog &#xff08;3&#xff09;运行工具 首先设置一下数据库连接的方式…
阅读更多...
【产品经理】APP上线准备内容及注意事项

【产品经理】APP上线准备内容及注意事项

在经历过漫长的开发过程后&#xff0c;APP终于上线了。此时不可掉以轻心&#xff0c;还有很多需要注意的事项&#xff0c;稍不留意有可能会功亏一篑。 一、APP功能注意事项 iOS审核指南&#xff1a;https://developer.APPle.com/cn/APP-store/review/guidelines/ Android每个…
阅读更多...
生信学院|07月19日《SOLIDWORKS方程式及全局变量的应用》

生信学院|07月19日《SOLIDWORKS方程式及全局变量的应用》

课程主题&#xff1a;SOLIDWORKS方程式及全局变量的应用 课程时间&#xff1a;2023年07月19日 14:00-14:30 主讲人&#xff1a;段厉蛟 生信科技 售后服务工程师 课程大纲&#xff1a; 1、SOLIDWORKS方程式及全局变量介绍 2、实例讲解 请安装腾讯会议客户端或APP&#xff…
阅读更多...
WebGPU开发简明教程【2023】

WebGPU开发简明教程【2023】

WebGPU 是一种全新的现代 API&#xff0c;用于在 Web 应用程序中访问 GPU 的功能。 在 WebGPU 之前&#xff0c;有 WebGL&#xff0c;它提供了 WebGPU 功能的子集。 它启用了新一类丰富的网络内容&#xff0c;开发人员用它构建了令人惊叹的东西。 然而&#xff0c;它基于 2007…
阅读更多...
HDFS Hadoop分布式文件存储系统整体概述

HDFS Hadoop分布式文件存储系统整体概述

HDFS 整体概述举例&#xff1a; 包括机架 rack1、rack2 包括5个Datanode,一个Namenode(主角色)带领5个Datanode(从角色)&#xff0c;每一个rack中包含不同的block模块文件为分块存储模式。块与块之间通过replication进行副本备份&#xff0c;进行冗余存储&#xff0c;Namenode…
阅读更多...
[Latex]newcommand\renewcommand\newtheorem的使用、总结、报错

[Latex]newcommand\renewcommand\newtheorem的使用、总结、报错

在Latex中经常使用一些自定义的名称&#xff0c;比如 \newtheorem{corollary}[theorem]{Corollary} %推论. 常用的定义类型的命令有&#xff1a; 命令含义举例备注\newcommand只用于定义新命令不能与现有命令重名\renrecommand只用于改变已有的命令的定义重定义已有命令或者定…
阅读更多...
Appium+Python+PO 设计模式

Appium+Python+PO 设计模式

目录 前言&#xff1a; 什么是 PageObject? 关于报告的输出 总结 前言&#xff1a; Appium是一个用于自动化移动应用程序测试的开源工具&#xff0c;Python是一种简单易学且功能强大的编程语言&#xff0c;PO&#xff08;Page Object&#xff09;设计模式是一种在自动化测…
阅读更多...
C进阶：指针的进阶（4）

C进阶：指针的进阶（4）

回调函数 回调函数就是一个通过函数指针调用的函数。&#xff08;函数指针的一个非常重要的作用就是实现回调函数&#xff09;。如果你把这个函数的指针&#xff08;地址&#xff09;作为参数传递给另一个函数&#xff0c;当这个指针被用来调用其所指向的函数时&#xff0c;我们…
阅读更多...
Mysql教程（二）：DDL学习

Mysql教程（二）：DDL学习

Mysql教程&#xff08;二&#xff09;&#xff1a;DDL学习 DDL &#xff08;Data Definition Language &#xff09;数据定义语言&#xff0c;用来定义数据库对象&#xff08;数据库、表、字段&#xff09; 1 DDL数据库操作 查询 查询所有数据库 SHOW DATABASES;查询当前数据…
阅读更多...
利用Python与ArcGIS工具进行蒸散发ET、植被总初级生产力GPP估算

利用Python与ArcGIS工具进行蒸散发ET、植被总初级生产力GPP估算

查看原文>>>基于”Python”多技术融合在蒸散发与植被总初级生产力估算中的实践应用 熟悉蒸散发ET及其组分&#xff08;植被蒸腾Ec、土壤蒸发Es、冠层截留Ei&#xff09;、植被总初级生产力GPP的概念和碳水耦合的基本原理&#xff1b;掌握利用Python与ArcGIS工具进行课…
阅读更多...
浅谈电能分项计量在节能降耗中的应用

浅谈电能分项计量在节能降耗中的应用

摘要&#xff1a;随着电力企业改革活动的持续推进&#xff0c;要想加快改革进程、优化改革效果&#xff0c;应该提高对节能降耗问题的关注度。在应用电力计量技术的过程中巧妙地渗透节能降耗这一理念&#xff0c;以此提高技术应用率&#xff0c;充分体现技术应用价值&#xff0…
阅读更多...
对象的方法

对象的方法

1.Object.assign(目标对象,源对象) 用于将所有可枚举的自身属性从一个或多个源对象复制到目标对象 目标对象——应用源属性的对象&#xff0c;修改后返回。 源对象——包含你要应用的属性的对象。 返回值&#xff1a;修改后的目标对象 const target { a: 1, b: 2 }; const …
阅读更多...
Win10我的电脑图标怎么调出来？5招搞定!

Win10我的电脑图标怎么调出来？5招搞定!

“我的电脑图标怎么突然不见啦&#xff1f;大家有没有遇到类似情况呀&#xff1f;请大家给我出出主意&#xff01;” 有的朋友可能会遇到这样一个问题&#xff0c;就是当我们更新了系统或进行某些操作后&#xff0c;计算机中【此电脑】的图标不见了。Win10我的电脑图标怎么调出…
阅读更多...
MySQL8.1.0版本正式发布，一起尝鲜新特性

MySQL8.1.0版本正式发布，一起尝鲜新特性

&#x1f4e2;&#x1f4e2;&#x1f4e2;&#x1f4e3;&#x1f4e3;&#x1f4e3; 哈喽&#xff01;大家好&#xff0c;我是【IT邦德】&#xff0c;江湖人称jeames007&#xff0c;10余年DBA工作经验 一位上进心十足的【大数据领域博主】&#xff01;&#x1f61c;&#x1f61…
阅读更多...
DT人体骨骼绑定

DT人体骨骼绑定

中心点 joint31.rotateXnurbsCircle4.rotateX*0.4; 选择控制器 控制器打组 骨骼打组 手柄也变小了 没变 打组 放组中心点 没做点约束的 正确了 IK和FK 可以移动 开启IK 关闭IK 创建控制器 在开启IK FK 旋转没反应 打组&#xff0c;设置中心点 隐藏不用的属性
阅读更多...
Spring Boot进阶(55)：SpringBoot之集成MongoDB及实战使用 | 超级详细，建议收藏

Spring Boot进阶(55)：SpringBoot之集成MongoDB及实战使用 | 超级详细，建议收藏

1. 前言&#x1f525; 前几期我们有介绍Mysql、Redis等数据库介绍及实战演示&#xff0c;对基本的数据存放有很好的共性&#xff0c;但是如果说遇到大面积的xml、Json、bson等格式文档数据存放&#xff0c;以上数据库并非是最优选择&#xff0c;最优选择是Mongodb数据库。 那么…
阅读更多...
【rk3568】uboot gpio寄存器配置

【rk3568】uboot gpio寄存器配置

假设GPIO4_C6 一、查看RM手册GPIO4C6关键字搜索 其中31-16位对应低16位是否可以写&#xff0c;&#xff08;为1就有写的权限&#xff0c;如gpio4C6 中10-8将31-16中对应位写1&#xff09; 二、查看GPIO4的基地址 三、找到GPIO4的基地址 四、GPIO4C6的地址就是sys_CRFoffset(0…
阅读更多...
Python 线程调用

Python 线程调用

简介&#xff1a; Python 线程可以通过主线程&#xff0c;调用线程来执行其他命令&#xff0c; 为Python提供更方便的使用。 并发线程测试 命令调用方式 import threading,time 定义每个线程要运行的函数 def run(n): print(“task”,n) time.sleep(1) 生成一个线程实例ta…
阅读更多...
【kafka调试】用命令行查看kafka是否发出了命令

【kafka调试】用命令行查看kafka是否发出了命令

server 10.10.90.210:9092 topic stream_manager_center_capture_file 摄像头id&#xff1a; 17283ed2a1ac685f9fd5ef9f0de04792 cd /usr/loca/kafka bin/kafka-console-consumer.sh --bootstrap-server 10.10.90.210:9092 --topic stream_manager_center_capture_file 然后添…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023