模拟行走机器人-python

news2025/1/18 8:58:35

leetcode第874题
链接https://leetcode.cn/problems/walking-robot-simulation

机器人在一个无限大小的 XY 网格平面上行走，从点 (0, 0) 处开始出发，面向北方。该机器人可以接收以下三种类型的命令 commands ：

-2 ：向左转 90 度
-1 ：向右转 90 度
1 <= x <= 9 ：向前移动 x 个单位长度

在网格上有一些格子被视为障碍物 obstacles 。第 i 个障碍物位于网格点 obstacles[i] = (xi, yi) 。
机器人无法走到障碍物上，它将会停留在障碍物的前一个网格方块上，但仍然可以继续尝试进行该路线的其余部分。返回从原点到机器人所有经过的路径点（坐标为整数）的最大欧式距离的平方。（即，如果距离为 5 ，则返回 25 ）

注意：

北表示 +Y 方向。
东表示 +X 方向。
南表示 -Y 方向。
西表示 -X 方向。

示例 1：

输入：commands = [4,-1,3], obstacles = []
输出：25
解释：
机器人开始位于 (0, 0)：
1. 向北移动 4 个单位，到达 (0, 4)
2. 右转
3. 向东移动 3 个单位，到达 (3, 4)
距离原点最远的是 (3, 4) ，距离为 32 + 42 = 25

示例 2：

输入：commands = [4,-1,4,-2,4], obstacles = [[2,4]]
输出：65
解释：机器人开始位于 (0, 0)：
1. 向北移动 4 个单位，到达 (0, 4)
2. 右转
3. 向东移动 1 个单位，然后被位于 (2, 4) 的障碍物阻挡，机器人停在 (1, 4)
4. 左转
5. 向北走 4 个单位，到达 (1, 8)
距离原点最远的是 (1, 8) ，距离为 12 + 82 = 65

提示：

1 <= commands.length <= 10^4
commands[i] is one of the values in the list [-2,-1,1,2,3,4,5,6,7,8,9].
0 <= obstacles.length <= 10^4
-3 * 104 <= xi, yi <= 3 * 10^4
答案保证小于 2^31

首先考虑暴力法，看全部遍历一遍能否获得答案
先将所有commands取出，然后直接对坐标一步到位进行移动，这显然是不好做的，因为一步到位的话，中间是否会遇到路障还不知道，如果遇到了，最后还得退到第一个路障，而且最终返回的是路径上距离原点最远的点，这已经暗示了想一步到位不太可能，应该一步一步地走。

那么一步一步的方式该如何实现，如何感知方向的变化应该是重点
我们将方向定义为0~3一共四个，当右转时加1，当左转时减1，四个方向对应不同的移动方向，可以用二维列表的下标来对应。

直接遍历所有的操作，如果碰到了路障就停止这个操作。
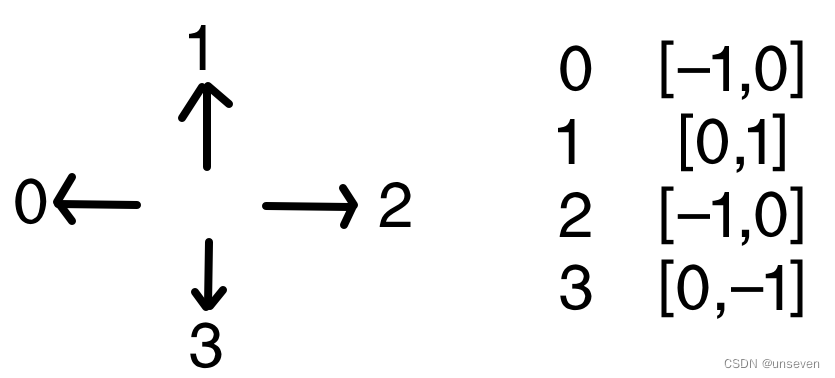
在这里插入图片描述

给出第一版的代码

class Solution:
    def robotSim(self, commands: [int], obstacles: [[int]]) -> int:
        d = [[-1,0],[0,1],[1,0],[0,-1]]
        toward,px,py,res=1,0,0,0
        for each in commands:
            if each < 0:
                toward += 1 if each == -1 else  -1
                toward %= 4
            else:
                for i in range(each):
                    if [px + d[toward][0],py + d[toward][1]] in obstacles:
                        break
                    px += d[toward][0]
                    py += d[toward][1]
                    res = max(res,px**2+py**2)
        return res

然而这将碰到超时的问题，主要是在判断前面是不是有障碍物，将障碍物列表改为集合类型即可

class Solution:
    def robotSim(self, commands: [int], obstacles: [[int]]) -> int:
        d = [[-1,0],[0,1],[1,0],[0,-1]]
        toward,px,py,res=1,0,0,0
        obstacles = [tuple(i) for i in obstacles]
        obstacles = set(obstacles)
        for each in commands:
            if each < 0:
                toward += 1 if each == -1 else  -1
                toward %= 4
            else:
                for i in range(each):
                    if tuple([px + d[toward][0],py + d[toward][1]]) in obstacles:
                        break
                    px += d[toward][0]
                    py += d[toward][1]
                    res = max(res,px**2+py**2)
        return res