完全二叉树

首先复习一下完全二叉树：数据从上到下，从左到右依次进行排列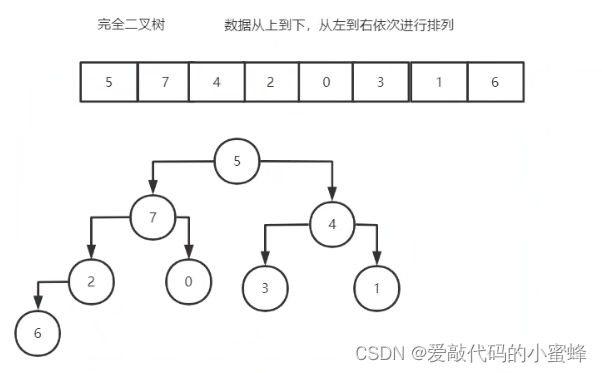

堆排序

第一步

利用完全二叉树构建大顶堆

大顶堆：父节点的值大于或等于其左右孩子的值（构建方法如下）

1.定义一个parent游标，让parent游标从后往前移动，直到有孩子节点停下来

2.定义parent的左孩子child，判断左孩子是否为空，有孩子，一定会有左孩子

3.如果左孩子不为空，判断有没有右孩子，如果有有孩子，那么左右孩子进行对比，child游标指向左右孩子的最大值

4.父节点和子节点进行对比，如果父节点的值大，就让parent继续往前移动；如果父节点的值小，就让父子节点的值进行交换，父节点指向子节点，子节点指向其左右孩子的最大值，如果child没有孩子，parent不再往下指

5.不断重复2-4步，直到大顶堆构建完成

第二步

让堆顶元素和堆底元素进行互换，互换完成之后，堆底元素不再参与构建

第三步

不断重复一二两步

源码

public class HeapSort {

	public static void main(String[] args) {
		
		int[] arr = new int[] {5,7,4,2,0,3,1,6};
		for(int p = arr.length-1;p >= 0;p--) {
			adjust(arr, p, arr.length);
		}
		
		//第二步
		for(int i = arr.length-1;i >= 0;i--) {
			int temp =arr[i];
			arr[i] = arr[0];
			arr[0] = temp;
			adjust(arr, 0, i);
		}
		
		System.out.println(Arrays.toString(arr));
		
	}
	public static void adjust(int[] arr,int parent,int length) {
		
		int Child = 2*parent+1;
		while(Child < length) {
			int rChild = Child +1;
			if(rChild < length && arr[rChild] > arr[Child]) {
				Child++;
			}
			
			if(arr[parent] < arr[Child]) {
				//父子节点进行交换
				int temp = arr[parent];
				arr[parent] = arr[Child];
				arr[Child] = temp;
				parent = Child;
				Child = 2*Child+1;
			}else {
				break;
			}
			
		}
	}
}