A - Adjacent SquaresA - Adjacent Squares
题目大意
给定一个由H行W列组成的网格。令(i,j)表示从上到下第i行,从左到右第j列的方块。找出与方块(R,C)共享边的方块数量。
这里,方块(a,b)和方块(c,d)被称为共享边,当且仅当|a-c|+|b-d|=1。
思路分析
与其列举不如排除。都不是则加4.
根据题目定义的共享边,我们只需要判断方块的位置是否在给定方块的上方、下方、左侧或右侧即可确定是否为共享边。
时间复杂度
O(1)
AC代码
#include<bits/stdc++.h>
using namespace std;
int main() {
int h, w, r, c;
cin >> h >> w >> r >> c;
int res = 0;
if (r != 1) res++;
if (r != h) res++;
if (c != 1) res++;
if (c != w) res++;
cout << res << endl;
return 0;
}
B - Enlarged Checker BoardB - Enlarged Checker Board
题目大意
给定了一个方块的布局规则和颜色填充规则,需要生成一个大小为(A×N)行(B×N)列的方块图案。
思路分析
大方块,再小方块
再把大方块按比例a,b分小
首先,根据给定的方块布局规则,创建一个n行n列的二维字符矩阵tile,用于表示每个小方块的颜色。然后,根据(A×N)行(B×N)列的尺寸,创建一个大小为(a×n)行(b×n)列的二维字符矩阵x,用于表示最终生成的方块图案。
接下来,通过遍历x矩阵,并根据矩阵元素的位置将对应的颜色填充到x矩阵中。具体地,对于x矩阵中的第i行第j列的元素,其对应的颜色是由tile矩阵中的(i/a)行(j/b)列的元素决定的。最后,按行输出x矩阵即可得到所需的方块图案。
时间复杂度
O(a×b×n^2)
- 创建tile矩阵的时间复杂度为O(n^2)
- 创建x矩阵的时间复杂度为O((a×n)×(b×n)) = O(a×b×n^2)
- 遍历x矩阵填充颜色的时间复杂度为O((a×n)×(b×n)) = O(a×b×n^2)
- 最终输出x矩阵的时间复杂度为O(a×n)
AC代码
#include<bits/stdc++.h>
using namespace std;
int main()
{
int n, a, b;
cin >> n >> a >> b;
// 创建tile矩阵并填充颜色
vector<string> tile(n, string(n, '-'));
for (int i = 0; i < n; i++)
{
if (i % 2 == 0)
{
for (int j = 0; j < n; j++)
{
if (j % 2 == 0)
tile[i][j] = '.';
else
tile[i][j] = '#';
}
}
else
{
for (int j = 0; j < n; j++)
{
if (j % 2 == 0)
tile[i][j] = '#';
else
tile[i][j] = '.';
}
}
}
// 创建x矩阵并填充颜色
vector<string> x(a * n, string(b * n, '-'));
for (int i = 0; i < a * n; i++)
{
for (int j = 0; j < b * n; j++)
{
x[i][j] = tile[i / a][j / b];
}
}
for (int i = 0; i < a * n; i++)
{
cout << x[i] << endl;
}
return 0;
}
C - Adjacent SwapsC - Adjacent Swaps
题目大意
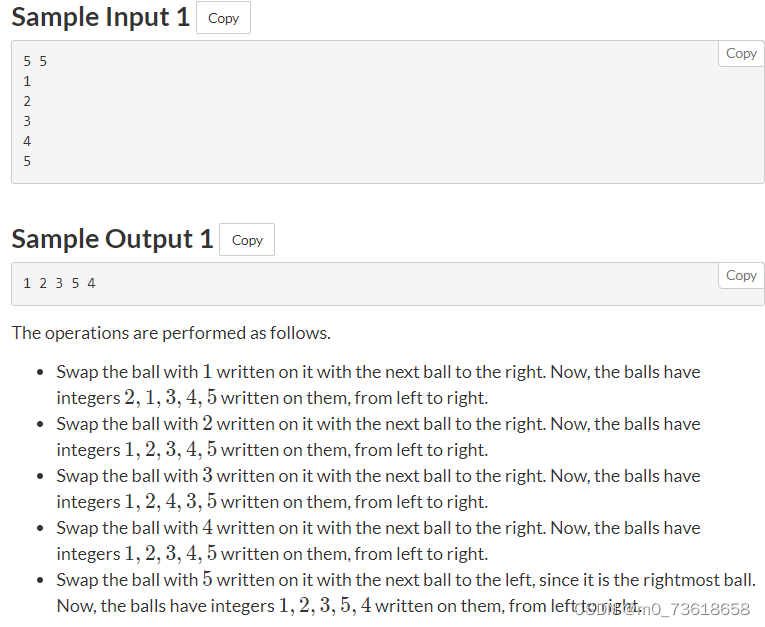
有 N 个小球从左到右排成一排,初始时每个小球上都写了一个整数 i(编号),表示它在初始时在第 i 个位置上。接下来进行 Q 次操作,每次操作给定一个整数 x,将编号为 x 的小球向右移动一位,若小球 x 已经在最右边,则将其移动到最左边。求经过 Q 次操作后小球的最终编号序列。
思路分析
对于每个小球,记录它当前所在的位置和它所携带的编号,分别用数组 idx 和 sta 来表示。初始时,第 i 个小球所携带的编号为 i,第 i 个小球当前所在的位置为 i。
对于每次操作,先记录要交换的数的编号,用a记录和位置(b)。如果小球 x 不在最右边,则将它和它右边的小球交换位置,同时更新 idx 数组和 sta 数组(用swap);否则,将小球 x 和它左边的小球交换位置,同时更新 idx 数组和 sta 数组。
最终,输出 sta 数组中的元素即可得到最终的编号序列。
时间复杂度
O(Q)
- 在每次操作中,只需要交换两个相邻元素的位置,因此每次操作的时间复杂度为 O(1)。总共执行 Q 次操作。
AC代码
#include<bits/stdc++.h>
using namespace std;
const int N=2*1e5+10;
int sta[N];
int idx[N];
int a,b;
int main()
{
int n,q;
cin>>n>>q;
for(int i=1;i<=n;i++){
sta[i]=i;
idx[i]=i;
}
while(q--)
{
int x;
cin>>x;
if(idx[x]!=n){
a=idx[x];b=sta[idx[x]+1];
swap(sta[idx[x]],sta[idx[x]+1]);//更新原数组
idx[x]=idx[x]+1;//更新坐标
idx[b]=a;
}else{
a=idx[x];b=sta[idx[x]-1];
swap(sta[idx[x]],sta[idx[x]-1]);
idx[x]=idx[x]-1;
idx[b]=a;
}
}
for(int i=1;i<=n;i++)
{cout<<sta[i]<<' ';
}
cout<<endl;
return 0;
}