运维专栏：运维小知识

目录

 1.🍁🍁用mv命令修改文件名

2.🍃🍃创建及删除文件夹即文件夹下所有文件

3.🍂🍂移动文件夹并重命名

4.🌿🌿复制文件

5.🍄🍄统计当前目录下文件的个数（不包含文件夹或子文件夹）

6.🌵🌵统计当前目录下文件的个数（包含子目录中的文件）

7.🌴🌴 查看当前路径下文件夹的个数（不包含子目录）

8.🌲🌲查看当前路径下文件夹（目录）的个数（包含子目录）

---

 1.🍁🍁用mv命令修改文件名

#将a.txt文件的文件名修改为a1.txt
mv a.txt a1.txt

2.🍃🍃创建及删除文件夹即文件夹下所有文件

#/home目录下创建文件夹packageA
mkdir /home/packageA

#在当前目录下创建a.txt文件
touch a.txt


#删除/home/packageA文件夹
rm -rf /home/packageA

#删除空文件夹home/packageC
rmdir /home/packageC

3.🍂🍂移动文件夹并重命名

# 将/home/packageA文件夹移动到根目录下，并重命名为packageB
mv /home/packageA /packageB  

4.🌿🌿复制文件

#将/home/packageA/下的所有文件复制到目录/home/cp/packageB/下
cp -r /home/packageA/* /home/cp/packageB/

#将/home/packageA/下的所有后缀为jpg文件复制到目录/home/cp/packageB/下
cp -r /home/packageA/*.jpg /home/cp/packageB/

5.🍄🍄统计当前目录下文件的个数（不包含文件夹或子文件夹）

ls -l  | grep "^-" | wc -l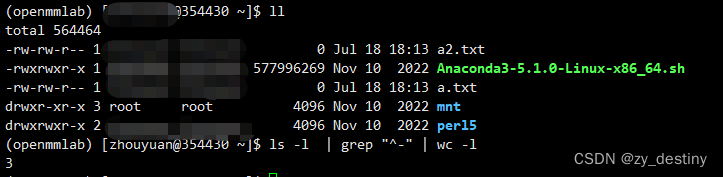

6.🌵🌵统计当前目录下文件的个数（包含子目录中的文件）

ls -lR | grep "^-" | wc -l

7.🌴🌴 查看当前路径下文件夹的个数（不包含子目录）

ls -l | grep "^d" | wc -l

8.🌲🌲查看当前路径下文件夹（目录）的个数（包含子目录）

ls -lR | grep "^d" | wc -l

整理不易，欢迎一键三连！！！

送你们一条美丽的--分割线--

---

🌷🌷🍀🍀🌾🌾🍓🍓🍂🍂🙋🙋🐸🐸🙋🙋💖💖🍌🍌🔔🔔🍉🍉🍭🍭🍋🍋🍇🍇🏆🏆📸📸⛵⛵⭐⭐🍎🍎👍👍🌷🌷